难度等级：容易

上一篇算法：

199. 二叉树的右视图【111】

力扣此题地址：

543. 二叉树的直径 - 力扣（Leetcode）

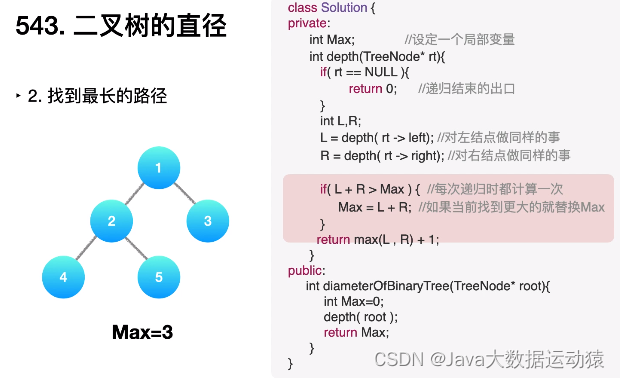
1.题目：543. 二叉树的直径

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

 

注意：两结点之间的路径长度是以它们之间边的数目表示。

 

2.解题思路：

拿这张图来讲解思路吧

首先要注意一点就是，最长路径可能穿过也可能不穿过根结点，如上图就是，它的最长路径就没有穿过根节点，而是【6,4,2,5,3】为它的最长路径。所以不能直接将root的左子节点和root的右子节点相加来得到最长路径。

注意这点之后，我们看下面这张图：

由上一步得出，我们不能直接将root的左子节点和root的右子节点相加来得到最长路径，所以我们要换一种思路，我们可以在depth方法中，每次走完 L=depth(rt->left) 和 R=depth(rt->right)时，做一个判断，如果L+R > Max的话，那么就相当于当前结点的左右子节点路径相加为最大，所以替换Max的值。

 

代码思路：

1.depth方法进入之后，先判断当前结点是否为null，也就是递归结束的出口

2.定义L 和R分别为当前结点的左右子节点，然后进行递归当前结点的左子树和右子树

3.每递归到一个节点，就判断当前结点的左右子节点的路径和是否为最大，进行替换

4.最终返回当前结点的深度，也就是max（L，R）+1

 

思路参考视频：

543. 二叉树的直径 - 力扣（Leetcode）

3.代码实现：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int Max = 0;
    public int diameterOfBinaryTree(TreeNode root) {
        depth(root);
        return Max;
    }

    public int depth(TreeNode node){
        if(node == null){
            return 0;//递归结束的出口，当访问到叶子结点的下一节点时
        }
        int L,R;
        L = depth(node.left);//对左子树递归
        R = depth(node.right);//对右子树递归

        // if(L + R > Max){//每次递归时都计算一次
        //     Max = L+R;//如果当前找到更大的就替换Max
        // }
        Max = Math.max(Max,L+R);
        return Math.max(L,R)+1;//当前结点的最大深度

    }
}