机器学习之利用SMO算法求解支持向量机

大家好，我是带我去滑雪！

本期将讨论支持向量机的实现问题，我们知道支持向量机的学习问题可以化为求解凸二次规划问题。这样的凸二次规划问题具有全局最优解，并且有许多最优化算法可以用于这一问题的求解。但是当训练样本容量很大时，这些算法往往变得非常低效，以致无法使用。所以，如何高效地实现支持向量机学习就成为一个重要的问题。目前人们已提出许多快速实现算法。本期讲述其中的序列最小最优化(sequential minimal optimization, SMO)算法。

1、SMO理论推导

2、python代码与实例

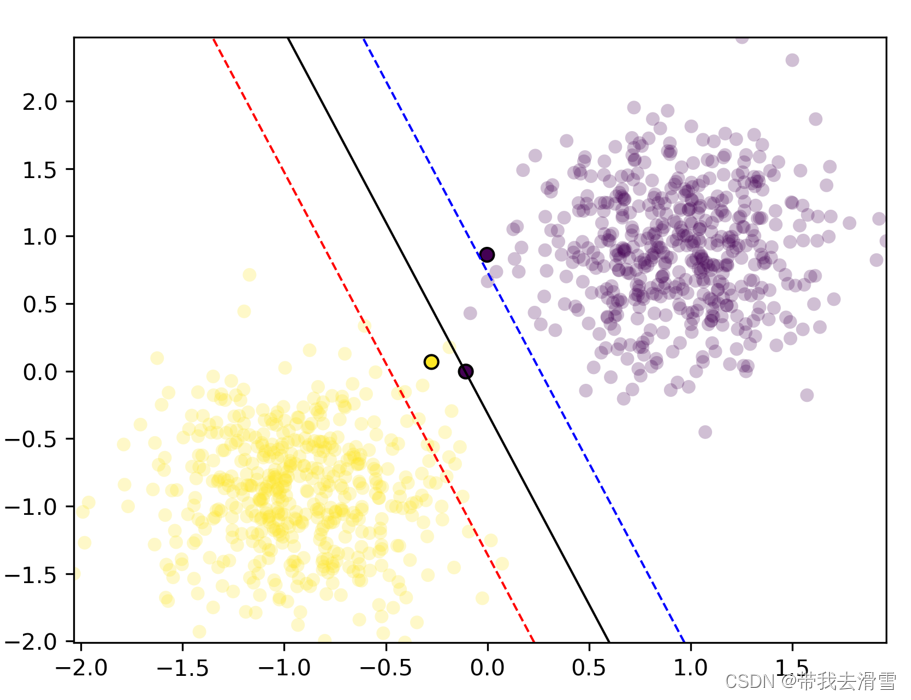
（1）使用线性可分样本，采用SMO算法求解支持向量机分类

（2）使用非线性数据（曲线），采用SMO算法求解支持向量机分类

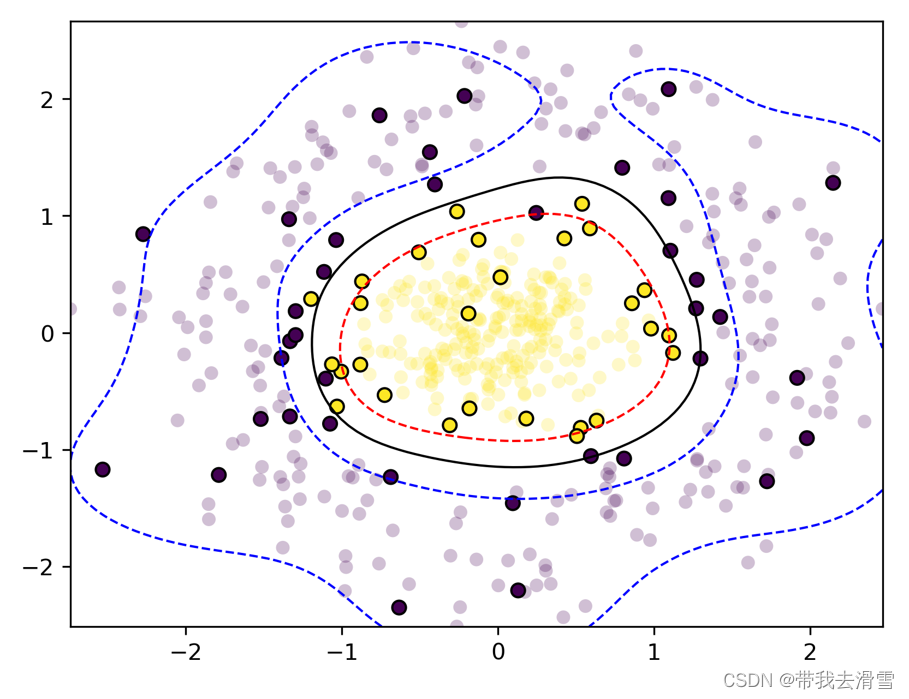
（3）使用非线性数据（交叉），采用SMO算法求解支持向量机分类

4、参考文献

1、SMO理论推导

SMO算法要求解如下凸二次规划对偶问题：

选择两个变量 $\alpha _{1}$ 、 $\alpha _{2}$ ,其他变量固定，于是SMO算法的最优化子问题就变成如下：

下面，首先求沿着约束方向未经剪辑即未考虑不等式约束时 $\alpha _{2}$ 的最优解 $\alpha _{1}^{new.unc}$ ；然后再求剪辑后的解 $\alpha _{2}^{new}$ 。我们用定理来叙述这个结果，为了叙述简单，引入记号记作：

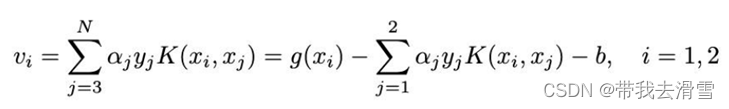
那么目标函数可写成如下形式：

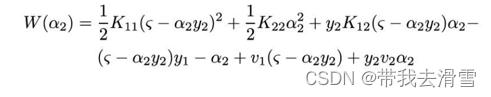
对 $\alpha _{2}$ 求导可得：

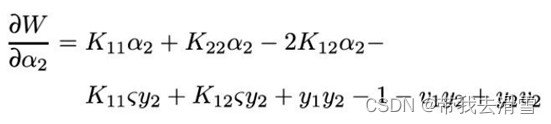
令其为0，得到：

因此， $\alpha _{2}$ 最终的解就是：

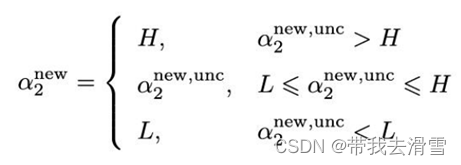
2、python代码与实例

（1）使用线性可分样本，采用SMO算法求解支持向量机分类

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs,make_circles,make_moons
from sklearn.preprocessing import StandardScaler



class SMOStruct:
"""构造SMO的数据结构"""
def __init__(self, X, y, C, kernel, alphas, b, errors, user_linear_optim):
self.X = X # 训练样本
self.y = y # 类别
self.C = C # 正则化常量，用于调整（过）拟合的程度
self.kernel = kernel # 核函数，实现了两个核函数，线性和高斯（RBF）
self.alphas = alphas # 拉格朗日乘子，与样本一一相对
self.b = b # 截距b
self.errors = errors # 差值矩阵，用于存储alpha值实际与预测值得差值，其数量与样本一一相对

self.m, self.n = np.shape(self.X) #m为训练样本的个数和n为样本的维度

self.user_linear_optim = user_linear_optim # 选择模型核函数，选择是，则使用线性核函数，否则使用RBF核函数（高斯核函数）
self.w = np.zeros(self.n) # 初始化权重w的值，主要用于线性核函数
#self.b = 0

def linear_kernel(x,y,b=1):
#线性核函数
""" returns the linear combination of arrays 'x' and 'y' with
the optional bias term 'b' (set to 1 by default). """
result = x @ y.T + b
return result # 注意矩阵乘法的@运算符



def gaussian_kernel(x,y, sigma=1):
#高斯核函数
"""设置默认sigma=1 """

if np.ndim(x) == 1 and np.ndim(y) == 1:
result = np.exp(-(np.linalg.norm(x-y,2))**2/(2*sigma**2))
elif(np.ndim(x)>1 and np.ndim(y) == 1) or (np.ndim(x) == 1 and np.ndim(y)>1):
result = np.exp(-(np.linalg.norm(x-y, 2, axis=1)**2)/(2*sigma**2))
elif np.ndim(x) > 1 and np.ndim(y) > 1 :
result = np.exp(-(np.linalg.norm(x[:, np.newaxis]- y[np.newaxis, :], 2, axis = 2) ** 2)/(2*sigma**2))
return result

#判别函数1，用于单一样本
def decision_function_output(model,i):
if model.user_linear_optim:
#Equation (J1)
#return float(np.dot(model.w.T, model.X[i])) - model.b
return float(model.w.T @ model.X[i]) - model.b
else:
#Equation (J10)
return np.sum([model.alphas[j] * model.y[j] * model.kernel(model.X[j], model.X[i]) for j in range(model.m)]) - model.b


# 判别函数2，用于多个样本
def decision_function(alphas, target, kernel, X_train, x_test, b):
""" Applies the SVM decision function to the input feature vectors in 'x_test'.
"""
result = (alphas * target) @ kernel(X_train, x_test) - b # *，@ 两个Operators的区别?

return result





def plot_decision_boundary(model, ax, resolution = 100, colors=('b','k','r'), levels = (-1, 0, 1)):
"""
画出分割平面及支持平面，
用的是等高线的方法

"""

#生成横坐标与纵坐标的网格[100x100]
#随后评估整个空间的模型
xrange = np.linspace(model.X[:,0].min(), model.X[:, 0].max(), resolution)#取样本当中横坐标x的最小值与最大值，均等分100份
yrange = np.linspace(model.X[:,1].min(), model.X[:, 1].max(), resolution)#取纵坐标的最小值与最大值，均等分100份
grid = [[decision_function(model.alphas,model.y, model.kernel, model.X,
np.array([xr,yr]), model.b) for xr in xrange] for yr in yrange]

grid = np.array(grid).reshape(len(xrange), len(yrange))

ax.contour(xrange, yrange, grid, levels=levels, linewidths = (1,1,1),
linestyles = ('--', '-', '--'), colors=colors) #绘制等高线，展示间隔
ax.scatter(model.X[:,0], model.X[:, 1],
c=model.y, cmap = plt.cm.viridis, lw=0, alpha =0.25) #绘制所有样本点的散点图

#as circled points (linewidth >0)
mask = np.round(model.alphas, decimals = 2) !=0.0
ax.scatter(model.X[mask,0], model.X[mask,1],
c=model.y[mask], cmap=plt.cm.viridis, lw=1, edgecolors='k')#画出支持向量（alpha不等于0的点）

return grid, ax





# 选择了alpha2、 alpha1后，开始第一步优化，然后迭代， “第二层循环，内循环”
# 主要的优化步骤在这里发生
def take_step(i1, i2, model):

#skip if chosen alphas are the same
if i1 == i2:
return 0, model
# a1, a2 的原值，old value，优化在于产生优化后的值，新值 new value

alph1 = model.alphas[i1]
alph2 = model.alphas[i2]

y1 = model.y[i1]
y2 = model.y[i2]

E1 = get_error(model, i1)
E2 = get_error(model, i2)
s = y1 * y2

# 计算alpha的边界，L, H
# compute L & H, the bounds on new possible alpha values
if(y1 != y2):
#y1,y2 异号，使用 Equation (J13)
L = max(0, alph2 - alph1)
H = min(model.C, model.C + alph2 - alph1)
elif (y1 == y2):
#y1,y2 同号，使用 Equation (J14)
L = max(0, alph1+alph2 - model.C)
H = min(model.C, alph1 + alph2)
if (L==H):
return 0, model

#分别计算样本1, 2对应的核函数组合，目的在于计算eta
#也就是求一阶导数后的值，目的在于计算a2new
k11 = model.kernel(model.X[i1], model.X[i1])
k12 = model.kernel(model.X[i1], model.X[i2])
k22 = model.kernel(model.X[i2], model.X[i2])
#计算 eta，equation (J15)
eta = k11 + k22 - 2*k12

#如论文中所述，分两种情况根据eta为正positive 还是为负或0来计算计算a2 new

if(eta>0):
#equation (J16) 计算alpha2
a2 = alph2 + y2 * (E1 - E2)/eta
#clip a2 based on bounds L & H
#把a2夹到限定区间 equation （J17）
if L < a2 < H:
a2 = a2
elif (a2 <= L):
a2 = L
elif (a2 >= H):
a2 = H
#如果eta不为正（为负或0）
#if eta is non-positive, move new a2 to bound with greater objective function value
else:
# Equation （J19）
# 在特殊情况下，eta可能不为正not be positive
f1 = y1*(E1 + model.b) - alph1*k11 - s*alph2*k12
f2 = y2 * (E2 + model.b) - s* alph1 * k12 - alph2 * k22

L1 = alph1 + s*(alph2 - L)
H1 = alph1 + s*(alph2 - H)

Lobj = L1 * f1 + L * f2 + 0.5 * (L1 ** 2) * k11 \
+ 0.5 * (L**2) * k22 + s * L * L1 * k12

Hobj = H1 * f1 + H * f2 + 0.5 * (H1**2) * k11 \
+ 0.5 * (H**2) * k22 + s * H * H1 * k12

if Lobj < Hobj - eps:
a2 = L
elif Lobj > Hobj + eps:
a2 = H
else:
a2 = alph2

#当new a2 千万分之一接近C或0是，就让它等于C或0
if a2 <1e-8:
a2 = 0.0
elif a2 > (model.C - 1e-8):
a2 = model.C
#超过容差仍不能优化时，跳过
#If examples can't be optimized within epsilon(eps), skip this pair
if (np.abs(a2 - alph2) < eps * (a2 + alph2 + eps)):
return 0, model
a1 = alph1 + s * (alph2 - a2) #根据新 a2计算新 a1 Equation(J18)
b1 = E1 + y1*(a1 - alph1) * k11 + y2 * (a2 - alph2) * k12 + model.b #更新截距b的值 Equation (J20)
b2 = E2 + y1*(a1 - alph1) * k12 + y2 * (a2 - alph2) * k22 + model.b #equation (J21)
# Set new threshoold based on if a1 or a2 is bound by L and/or H
if 0 < a1 and a1 < C:
b_new =b1
elif 0 < a2 and a2 < C:
b_new = b2
#Average thresholds if both are bound
else:
b_new = (b1 + b2) * 0.5
#update model threshold
model.b = b_new
# 当所训练模型为线性核函数时
#Equation (J22) 计算w的值
if model.user_linear_optim:
model.w = model.w + y1 * (a1 - alph1)*model.X[i1] + y2 * (a2 - alph2) * model.X[i2]
#在alphas矩阵中分别更新a1, a2的值
#Update model object with new alphas & threshold
model.alphas[i1] = a1
model.alphas[i2] = a2
#优化完成，更新差值矩阵的对应值
#同时更新差值矩阵其它值
model.errors[i1] = 0
model.errors[i2] = 0
#更新差值 Equation (12)
for i in range(model.m):
if 0 < model.alphas[i] < model.C:
model.errors[i] += y1*(a1 - alph1)*model.kernel(model.X[i1],model.X[i]) + \
y2*(a2 - alph2)*model.kernel(model.X[i2], model.X[i]) + model.b - b_new
return 1, model

def get_error(model, i1):
if 0< model.alphas[i1] <model.C:
return model.errors[i1]
else:
return decision_function_output(model,i1) - model.y[i1]



def examine_example(i2, model):
y2 = model.y[i2]
alph2 = model.alphas[i2]
E2 = get_error(model, i2)
r2 = E2 * y2
#重点：这一段的重点在于确定 alpha1, 也就是old a1，并送到take_step去analytically 优化
# 下面条件之一满足，进入if开始找第二个alpha，送到take_step进行优化
if ((r2 < -tol and alph2 < model.C) or (r2 > tol and alph2 > 0)):
if len(model.alphas[(model.alphas != 0) & (model.alphas != model.C)]) > 1:#筛选器
#选择Ei矩阵中差值最大的先进性优化
# 要想|E1-E2|最大，只需要在E2为正时，选择最小的Ei作为E1
# 在E2为负时选择最大的Ei作为E1
if model.errors[i2] > 0:
i1 = np.argmin(model.errors)
elif model.errors[i2] <= 0:
i1 = np.argmax(model.errors)
step_result,model = take_step(i1,i2, model)
if step_result:
return 1, model
# 循环所有非0 非C alphas值进行优化，随机选择起始点
for i1 in np.roll(np.where((model.alphas != 0) & (model.alphas != model.C))[0],
np.random.choice(np.arange(model.m))):
step_result, model = take_step(i1, i2, model)
if step_result:
return 1, model

#alpha2确定的情况下，如何选择alpha1? 循环所有(m-1) alphas, 随机选择起始点
for i1 in np.roll(np.arange(model.m), np.random.choice(np.arange(model.m))):
#print("what is the first i1",i1)
step_result, model = take_step(i1, i2, model)

if step_result:
return 1, model
#先看最上面的if语句，如果if条件不满足，说明KKT条件已满足，找其它样本进行优化，则执行下面这句，退出
return 0, model

#核心函数
def fit(model):

numChanged = 0 #numChanged存放优化返回的结果，如果优化成功，则返回1，反之为0
examineAll = 1 #examineAll表示从0号元素开始优化，如果所有都优化完成，则赋值为0
#loop num record
#计数器，记录优化时的循环次数
loopnum = 0
loopnum1 = 0
loopnum2 = 0
# 当numChanged = 0 and examineAll = 0时循环退出
# 实际是顺序地执行完所有的样本，也就是第一个if中的循环，
# 并且 else中的循环没有可优化的alpha，目标函数收敛了：在容差之内，并且满足KKT条件
# 则循环退出，如果执行2000次循环仍未收敛，也退出
# 重点：这段的重点在于确定 alpha2，也就是old a 2, 或者说alpha2的下标，old a2和old a1都是heuristically 选择
while(numChanged > 0) or (examineAll):
numChanged = 0
if loopnum == 2000:#设置循环次数
break
loopnum = loopnum + 1
if examineAll:
loopnum1 = loopnum1 + 1 # 记录顺序一个一个选择alpha2时的循环次数
# # 从0,1,2,3,...,m顺序选择a2的，送给examine_example选择alpha1，总共m(m-1)种选法
for i in range(model.alphas.shape[0]):
examine_result, model = examine_example(i, model)
numChanged += examine_result
else: #上面if里m(m-1)执行完的后执行
loopnum2 = loopnum2 + 1
# loop over examples where alphas are not already at their limits
for i in np.where((model.alphas != 0) & (model.alphas != model.C))[0]:#筛选器，用于筛选alpha
examine_result, model = examine_example(i, model)
numChanged += examine_result
if examineAll == 1:
examineAll = 0
elif numChanged == 0:
examineAll = 1
print("loopnum012",loopnum,":", loopnum1,":", loopnum2)
return model
# can be replaced as per different model u want to show

#主程序部分
# 生成测试数据，训练样本
X_train, y = make_blobs(n_samples = 1000, centers =2, n_features=2, random_state = 3)
#make_blobs表示是 sklearn.datasets中的一个函数，主要是产生聚类数据集，产生一个数据集和相应的标签
#random_state表示可以固定生成的数据，给定数之后，每次生成的数据集就是固定的
# center表示标签的种类数

scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train, y)# 标准化，训练样本异常大或异常小会影响样本的正确训练，如果数据的分布很分散也会影响
y=2*y-1#按照支持向量机惯例，将响应变量的取值由{0，1}变换为{-1，1}
# set model parameters and initial values
C = 20.0 #为一个超参数，惩罚参数，自行设定
m = len(X_train_scaled)#计算标准化后训练集的个数
initial_alphas=np.zeros(m)#定义初始化alpha，返回一个元素全为0且长度等于训练集个数的数组，我们的目标就是找所有的alpha值，使目标函数最优，
#只有样本点在间隔内才不为0，其他均为0
initial_b=0.0#初始化截距
tol = 0.01 # #软间隔优化目标的ε允许样本错误的参数
eps = 0.01 # 设置允许的终止判据（默认为0.001）
#初始化smo数据结构
model = SMOStruct(X_train_scaled, y, C, linear_kernel, initial_alphas, initial_b, np.zeros(m),user_linear_optim=True)
#print("model created ...")
#初始化差错矩阵，调用判别函数，差错矩阵为预测值与真实值的的差
initial_error = decision_function(model.alphas, model.y, model.kernel, model.X, model.X, model.b) - model.y
model.errors = initial_error
np.random.seed(0)
#主函数到此结束

# 初始化smo结构，使用高斯核函数
model = SMOStruct(X_train_scaled, y, C, lambda x, y: gaussian_kernel(x,y,sigma=0.5),
initial_alphas, initial_b, np.zeros(m), user_linear_optim=False)

#initialize error cache
initial_error = decision_function(model.alphas, model.y, model.kernel,
model.X, model.X, model.b) - model.y
model.errors = initial_error

print("开始拟合模型...")
#开始训练
output = fit(model)
#绘制训练完，找到分割平面的图
fig,ax = plt.subplots()
grid,ax = plot_decision_boundary(output, ax)
plt.savefig("squares1.png",
bbox_inches ="tight",
pad_inches = 1,
transparent = True,
facecolor ="w",
edgecolor ='w',
dpi=300,
orientation ='landscape')

输出结果：
开始拟合模型...
loopnum012 2000 : 1 : 1999

（2）使用非线性数据（曲线），采用SMO算法求解支持向量机分类

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs,make_circles,make_moons
from sklearn.preprocessing import StandardScaler



class SMOStruct:
"""构造SMO的数据结构"""
def __init__(self, X, y, C, kernel, alphas, b, errors, user_linear_optim):
self.X = X # 训练样本
self.y = y # 类别
self.C = C # 正则化常量，用于调整（过）拟合的程度
self.kernel = kernel # 核函数，实现了两个核函数，线性和高斯（RBF）
self.alphas = alphas # 拉格朗日乘子，与样本一一相对
self.b = b # 截距b
self.errors = errors # 差值矩阵，用于存储alpha值实际与预测值得差值，其数量与样本一一相对

self.m, self.n = np.shape(self.X) #m为训练样本的个数和n为样本的维度

self.user_linear_optim = user_linear_optim # 选择模型核函数，选择是，则使用线性核函数，否则使用RBF核函数（高斯核函数）
self.w = np.zeros(self.n) # 初始化权重w的值，主要用于线性核函数
#self.b = 0

def linear_kernel(x,y,b=1):
#线性核函数
""" returns the linear combination of arrays 'x' and 'y' with
the optional bias term 'b' (set to 1 by default). """
result = x @ y.T + b
return result # 注意矩阵乘法的@运算符



def gaussian_kernel(x,y, sigma=1):
#高斯核函数
"""设置默认sigma=1 """

if np.ndim(x) == 1 and np.ndim(y) == 1:
result = np.exp(-(np.linalg.norm(x-y,2))**2/(2*sigma**2))
elif(np.ndim(x)>1 and np.ndim(y) == 1) or (np.ndim(x) == 1 and np.ndim(y)>1):
result = np.exp(-(np.linalg.norm(x-y, 2, axis=1)**2)/(2*sigma**2))
elif np.ndim(x) > 1 and np.ndim(y) > 1 :
result = np.exp(-(np.linalg.norm(x[:, np.newaxis]- y[np.newaxis, :], 2, axis = 2) ** 2)/(2*sigma**2))
return result

#判别函数1，用于单一样本
def decision_function_output(model,i):
if model.user_linear_optim:
#Equation (J1)
#return float(np.dot(model.w.T, model.X[i])) - model.b
return float(model.w.T @ model.X[i]) - model.b
else:
#Equation (J10)
return np.sum([model.alphas[j] * model.y[j] * model.kernel(model.X[j], model.X[i]) for j in range(model.m)]) - model.b


# 判别函数2，用于多个样本
def decision_function(alphas, target, kernel, X_train, x_test, b):
""" Applies the SVM decision function to the input feature vectors in 'x_test'.
"""
result = (alphas * target) @ kernel(X_train, x_test) - b # *，@ 两个Operators的区别?

return result





def plot_decision_boundary(model, ax, resolution = 100, colors=('b','k','r'), levels = (-1, 0, 1)):
"""
画出分割平面及支持平面，
用的是等高线的方法

"""

#生成横坐标与纵坐标的网格[100x100]
#随后评估整个空间的模型
xrange = np.linspace(model.X[:,0].min(), model.X[:, 0].max(), resolution)#取样本当中横坐标x的最小值与最大值，均等分100份
yrange = np.linspace(model.X[:,1].min(), model.X[:, 1].max(), resolution)#取纵坐标的最小值与最大值，均等分100份
grid = [[decision_function(model.alphas,model.y, model.kernel, model.X,
np.array([xr,yr]), model.b) for xr in xrange] for yr in yrange]

grid = np.array(grid).reshape(len(xrange), len(yrange))

ax.contour(xrange, yrange, grid, levels=levels, linewidths = (1,1,1),
linestyles = ('--', '-', '--'), colors=colors) #绘制等高线，展示间隔
ax.scatter(model.X[:,0], model.X[:, 1],
c=model.y, cmap = plt.cm.viridis, lw=0, alpha =0.25) #绘制所有样本点的散点图

#as circled points (linewidth >0)
mask = np.round(model.alphas, decimals = 2) !=0.0
ax.scatter(model.X[mask,0], model.X[mask,1],
c=model.y[mask], cmap=plt.cm.viridis, lw=1, edgecolors='k')#画出支持向量（alpha不等于0的点）

return grid, ax




# 选择了alpha2、 alpha1后，开始第一步优化，然后迭代， “第二层循环，内循环”
# 主要的优化步骤在这里发生
def take_step(i1, i2, model):

#skip if chosen alphas are the same
if i1 == i2:
return 0, model
# a1, a2 的原值，old value，优化在于产生优化后的值，新值 new value

alph1 = model.alphas[i1]
alph2 = model.alphas[i2]

y1 = model.y[i1]
y2 = model.y[i2]

E1 = get_error(model, i1)
E2 = get_error(model, i2)
s = y1 * y2

# 计算alpha的边界，L, H
# compute L & H, the bounds on new possible alpha values
if(y1 != y2):
#y1,y2 异号，使用 Equation (J13)
L = max(0, alph2 - alph1)
H = min(model.C, model.C + alph2 - alph1)
elif (y1 == y2):
#y1,y2 同号，使用 Equation (J14)
L = max(0, alph1+alph2 - model.C)
H = min(model.C, alph1 + alph2)
if (L==H):
return 0, model

#分别计算样本1, 2对应的核函数组合，目的在于计算eta
#也就是求一阶导数后的值，目的在于计算a2new
k11 = model.kernel(model.X[i1], model.X[i1])
k12 = model.kernel(model.X[i1], model.X[i2])
k22 = model.kernel(model.X[i2], model.X[i2])
#计算 eta，equation (J15)
eta = k11 + k22 - 2*k12

#如论文中所述，分两种情况根据eta为正positive 还是为负或0来计算计算a2 new

if(eta>0):
#equation (J16) 计算alpha2
a2 = alph2 + y2 * (E1 - E2)/eta
#clip a2 based on bounds L & H
#把a2夹到限定区间 equation （J17）
if L < a2 < H:
a2 = a2
elif (a2 <= L):
a2 = L
elif (a2 >= H):
a2 = H
#如果eta不为正（为负或0）
#if eta is non-positive, move new a2 to bound with greater objective function value
else:
# Equation （J19）
# 在特殊情况下，eta可能不为正not be positive
f1 = y1*(E1 + model.b) - alph1*k11 - s*alph2*k12
f2 = y2 * (E2 + model.b) - s* alph1 * k12 - alph2 * k22

L1 = alph1 + s*(alph2 - L)
H1 = alph1 + s*(alph2 - H)

Lobj = L1 * f1 + L * f2 + 0.5 * (L1 ** 2) * k11 \
+ 0.5 * (L**2) * k22 + s * L * L1 * k12

Hobj = H1 * f1 + H * f2 + 0.5 * (H1**2) * k11 \
+ 0.5 * (H**2) * k22 + s * H * H1 * k12

if Lobj < Hobj - eps:
a2 = L
elif Lobj > Hobj + eps:
a2 = H
else:
a2 = alph2

#当new a2 千万分之一接近C或0是，就让它等于C或0
if a2 <1e-8:
a2 = 0.0
elif a2 > (model.C - 1e-8):
a2 = model.C
#超过容差仍不能优化时，跳过
#If examples can't be optimized within epsilon(eps), skip this pair
if (np.abs(a2 - alph2) < eps * (a2 + alph2 + eps)):
return 0, model
a1 = alph1 + s * (alph2 - a2) #根据新 a2计算新 a1 Equation(J18)
b1 = E1 + y1*(a1 - alph1) * k11 + y2 * (a2 - alph2) * k12 + model.b #更新截距b的值 Equation (J20)
b2 = E2 + y1*(a1 - alph1) * k12 + y2 * (a2 - alph2) * k22 + model.b #equation (J21)
# Set new threshoold based on if a1 or a2 is bound by L and/or H
if 0 < a1 and a1 < C:
b_new =b1
elif 0 < a2 and a2 < C:
b_new = b2
#Average thresholds if both are bound
else:
b_new = (b1 + b2) * 0.5
#update model threshold
model.b = b_new
# 当所训练模型为线性核函数时
#Equation (J22) 计算w的值
if model.user_linear_optim:
model.w = model.w + y1 * (a1 - alph1)*model.X[i1] + y2 * (a2 - alph2) * model.X[i2]
#在alphas矩阵中分别更新a1, a2的值
#Update model object with new alphas & threshold
model.alphas[i1] = a1
model.alphas[i2] = a2
#优化完成，更新差值矩阵的对应值
#同时更新差值矩阵其它值
model.errors[i1] = 0
model.errors[i2] = 0
#更新差值 Equation (12)
for i in range(model.m):
if 0 < model.alphas[i] < model.C:
model.errors[i] += y1*(a1 - alph1)*model.kernel(model.X[i1],model.X[i]) + \
y2*(a2 - alph2)*model.kernel(model.X[i2], model.X[i]) + model.b - b_new
return 1, model

def get_error(model, i1):
if 0< model.alphas[i1] <model.C:
return model.errors[i1]
else:
return decision_function_output(model,i1) - model.y[i1]



def examine_example(i2, model):
y2 = model.y[i2]
alph2 = model.alphas[i2]
E2 = get_error(model, i2)
r2 = E2 * y2
#重点：这一段的重点在于确定 alpha1, 也就是old a1，并送到take_step去analytically 优化
# 下面条件之一满足，进入if开始找第二个alpha，送到take_step进行优化
if ((r2 < -tol and alph2 < model.C) or (r2 > tol and alph2 > 0)):
if len(model.alphas[(model.alphas != 0) & (model.alphas != model.C)]) > 1:#筛选器
#选择Ei矩阵中差值最大的先进性优化
# 要想|E1-E2|最大，只需要在E2为正时，选择最小的Ei作为E1
# 在E2为负时选择最大的Ei作为E1
if model.errors[i2] > 0:
i1 = np.argmin(model.errors)
elif model.errors[i2] <= 0:
i1 = np.argmax(model.errors)
step_result,model = take_step(i1,i2, model)
if step_result:
return 1, model
# 循环所有非0 非C alphas值进行优化，随机选择起始点
for i1 in np.roll(np.where((model.alphas != 0) & (model.alphas != model.C))[0],
np.random.choice(np.arange(model.m))):
step_result, model = take_step(i1, i2, model)
if step_result:
return 1, model

#alpha2确定的情况下，如何选择alpha1? 循环所有(m-1) alphas, 随机选择起始点
for i1 in np.roll(np.arange(model.m), np.random.choice(np.arange(model.m))):
#print("what is the first i1",i1)
step_result, model = take_step(i1, i2, model)

if step_result:
return 1, model
#先看最上面的if语句，如果if条件不满足，说明KKT条件已满足，找其它样本进行优化，则执行下面这句，退出
return 0, model

#核心函数
def fit(model):

numChanged = 0 #numChanged存放优化返回的结果，如果优化成功，则返回1，反之为0
examineAll = 1 #examineAll表示从0号元素开始优化，如果所有都优化完成，则赋值为0
#loop num record
#计数器，记录优化时的循环次数
loopnum = 0
loopnum1 = 0
loopnum2 = 0
# 当numChanged = 0 and examineAll = 0时循环退出
# 实际是顺序地执行完所有的样本，也就是第一个if中的循环，
# 并且 else中的循环没有可优化的alpha，目标函数收敛了：在容差之内，并且满足KKT条件
# 则循环退出，如果执行2000次循环仍未收敛，也退出
# 重点：这段的重点在于确定 alpha2，也就是old a 2, 或者说alpha2的下标，old a2和old a1都是heuristically 选择
while(numChanged > 0) or (examineAll):
numChanged = 0
if loopnum == 2000:#设置循环次数
break
loopnum = loopnum + 1
if examineAll:
loopnum1 = loopnum1 + 1 # 记录顺序一个一个选择alpha2时的循环次数
# # 从0,1,2,3,...,m顺序选择a2的，送给examine_example选择alpha1，总共m(m-1)种选法
for i in range(model.alphas.shape[0]):
examine_result, model = examine_example(i, model)
numChanged += examine_result
else: #上面if里m(m-1)执行完的后执行
loopnum2 = loopnum2 + 1
# loop over examples where alphas are not already at their limits
for i in np.where((model.alphas != 0) & (model.alphas != model.C))[0]:#筛选器，用于筛选alpha
examine_result, model = examine_example(i, model)
numChanged += examine_result
if examineAll == 1:
examineAll = 0
elif numChanged == 0:
examineAll = 1
print("loopnum012",loopnum,":", loopnum1,":", loopnum2)
return model
# can be replaced as per different model u want to show

#产生非线性数据，交叉的
X_train,y = make_moons(n_samples = 500, noise=0.2,
random_state =1)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train, y)
y=2*y-1

#print('X_train',':', X_train)
# print('y',':',y)

#Set model parameters and initial values
C = 1.0
m = len(X_train_scaled)
initial_alphas = np.zeros(m)
initial_b = 0.0

# Set tolerances
tol = 0.01 # error tolerance
eps = 0.01 # alpha tolerance

# 初始化smo结构，使用高斯核函数
model = SMOStruct(X_train_scaled, y, C, lambda x, y: gaussian_kernel(x,y,sigma=0.5),
initial_alphas, initial_b, np.zeros(m), user_linear_optim=False)

#initialize error cache
#先把这个注释掉
initial_error = decision_function(model.alphas, model.y, model.kernel,
model.X, model.X, model.b) - model.y
model.errors = initial_error

print("开始拟合模型...")
#开始训练
output = fit(model)
#绘制训练完，找到分割平面的图
fig,ax = plt.subplots()
grid,ax = plot_decision_boundary(output, ax)

plt.savefig("squares1.png",
bbox_inches ="tight",
pad_inches = 1,
transparent = True,
facecolor ="w",
edgecolor ='w',
dpi=300,
orientation ='landscape')

输出结果：
开始拟合模型...
loopnum012 2000 : 9 : 1991

（3）使用非线性数据（交叉），采用SMO算法求解支持向量机分类

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs,make_circles,make_moons
from sklearn.preprocessing import StandardScaler



class SMOStruct:
"""构造SMO的数据结构"""
def __init__(self, X, y, C, kernel, alphas, b, errors, user_linear_optim):
self.X = X # 训练样本
self.y = y # 类别
self.C = C # 正则化常量，用于调整（过）拟合的程度
self.kernel = kernel # 核函数，实现了两个核函数，线性和高斯（RBF）
self.alphas = alphas # 拉格朗日乘子，与样本一一相对
self.b = b # 截距b
self.errors = errors # 差值矩阵，用于存储alpha值实际与预测值得差值，其数量与样本一一相对

self.m, self.n = np.shape(self.X) #m为训练样本的个数和n为样本的维度

self.user_linear_optim = user_linear_optim # 选择模型核函数，选择是，则使用线性核函数，否则使用RBF核函数（高斯核函数）
self.w = np.zeros(self.n) # 初始化权重w的值，主要用于线性核函数
#self.b = 0

def linear_kernel(x,y,b=1):
#线性核函数
""" returns the linear combination of arrays 'x' and 'y' with
the optional bias term 'b' (set to 1 by default). """
result = x @ y.T + b
return result # 注意矩阵乘法的@运算符



def gaussian_kernel(x,y, sigma=1):
#高斯核函数
"""设置默认sigma=1 """

if np.ndim(x) == 1 and np.ndim(y) == 1:
result = np.exp(-(np.linalg.norm(x-y,2))**2/(2*sigma**2))
elif(np.ndim(x)>1 and np.ndim(y) == 1) or (np.ndim(x) == 1 and np.ndim(y)>1):
result = np.exp(-(np.linalg.norm(x-y, 2, axis=1)**2)/(2*sigma**2))
elif np.ndim(x) > 1 and np.ndim(y) > 1 :
result = np.exp(-(np.linalg.norm(x[:, np.newaxis]- y[np.newaxis, :], 2, axis = 2) ** 2)/(2*sigma**2))
return result

#判别函数1，用于单一样本
def decision_function_output(model,i):
if model.user_linear_optim:
#Equation (J1)
#return float(np.dot(model.w.T, model.X[i])) - model.b
return float(model.w.T @ model.X[i]) - model.b
else:
#Equation (J10)
return np.sum([model.alphas[j] * model.y[j] * model.kernel(model.X[j], model.X[i]) for j in range(model.m)]) - model.b


# 判别函数2，用于多个样本
def decision_function(alphas, target, kernel, X_train, x_test, b):
""" Applies the SVM decision function to the input feature vectors in 'x_test'.
"""
result = (alphas * target) @ kernel(X_train, x_test) - b # *，@ 两个Operators的区别?

return result





def plot_decision_boundary(model, ax, resolution = 100, colors=('b','k','r'), levels = (-1, 0, 1)):
"""
画出分割平面及支持平面，
用的是等高线的方法

"""

#生成横坐标与纵坐标的网格[100x100]
#随后评估整个空间的模型
xrange = np.linspace(model.X[:,0].min(), model.X[:, 0].max(), resolution)#取样本当中横坐标x的最小值与最大值，均等分100份
yrange = np.linspace(model.X[:,1].min(), model.X[:, 1].max(), resolution)#取纵坐标的最小值与最大值，均等分100份
grid = [[decision_function(model.alphas,model.y, model.kernel, model.X,
np.array([xr,yr]), model.b) for xr in xrange] for yr in yrange]

grid = np.array(grid).reshape(len(xrange), len(yrange))

ax.contour(xrange, yrange, grid, levels=levels, linewidths = (1,1,1),
linestyles = ('--', '-', '--'), colors=colors) #绘制等高线，展示间隔
ax.scatter(model.X[:,0], model.X[:, 1],
c=model.y, cmap = plt.cm.viridis, lw=0, alpha =0.25) #绘制所有样本点的散点图

#as circled points (linewidth >0)
mask = np.round(model.alphas, decimals = 2) !=0.0
ax.scatter(model.X[mask,0], model.X[mask,1],
c=model.y[mask], cmap=plt.cm.viridis, lw=1, edgecolors='k')#画出支持向量（alpha不等于0的点）

return grid, ax





# 选择了alpha2、 alpha1后，开始第一步优化，然后迭代， “第二层循环，内循环”
# 主要的优化步骤在这里发生
def take_step(i1, i2, model):

#skip if chosen alphas are the same
if i1 == i2:
return 0, model
# a1, a2 的原值，old value，优化在于产生优化后的值，新值 new value

alph1 = model.alphas[i1]
alph2 = model.alphas[i2]

y1 = model.y[i1]
y2 = model.y[i2]

E1 = get_error(model, i1)
E2 = get_error(model, i2)
s = y1 * y2

# 计算alpha的边界，L, H
# compute L & H, the bounds on new possible alpha values
if(y1 != y2):
#y1,y2 异号，使用 Equation (J13)
L = max(0, alph2 - alph1)
H = min(model.C, model.C + alph2 - alph1)
elif (y1 == y2):
#y1,y2 同号，使用 Equation (J14)
L = max(0, alph1+alph2 - model.C)
H = min(model.C, alph1 + alph2)
if (L==H):
return 0, model

#分别计算样本1, 2对应的核函数组合，目的在于计算eta
#也就是求一阶导数后的值，目的在于计算a2new
k11 = model.kernel(model.X[i1], model.X[i1])
k12 = model.kernel(model.X[i1], model.X[i2])
k22 = model.kernel(model.X[i2], model.X[i2])
#计算 eta，equation (J15)
eta = k11 + k22 - 2*k12

#如论文中所述，分两种情况根据eta为正positive 还是为负或0来计算计算a2 new

if(eta>0):
#equation (J16) 计算alpha2
a2 = alph2 + y2 * (E1 - E2)/eta
#clip a2 based on bounds L & H
#把a2夹到限定区间 equation （J17）
if L < a2 < H:
a2 = a2
elif (a2 <= L):
a2 = L
elif (a2 >= H):
a2 = H
#如果eta不为正（为负或0）
#if eta is non-positive, move new a2 to bound with greater objective function value
else:
# Equation （J19）
# 在特殊情况下，eta可能不为正not be positive
f1 = y1*(E1 + model.b) - alph1*k11 - s*alph2*k12
f2 = y2 * (E2 + model.b) - s* alph1 * k12 - alph2 * k22

L1 = alph1 + s*(alph2 - L)
H1 = alph1 + s*(alph2 - H)

Lobj = L1 * f1 + L * f2 + 0.5 * (L1 ** 2) * k11 \
+ 0.5 * (L**2) * k22 + s * L * L1 * k12

Hobj = H1 * f1 + H * f2 + 0.5 * (H1**2) * k11 \
+ 0.5 * (H**2) * k22 + s * H * H1 * k12

if Lobj < Hobj - eps:
a2 = L
elif Lobj > Hobj + eps:
a2 = H
else:
a2 = alph2

#当new a2 千万分之一接近C或0是，就让它等于C或0
if a2 <1e-8:
a2 = 0.0
elif a2 > (model.C - 1e-8):
a2 = model.C
#超过容差仍不能优化时，跳过
#If examples can't be optimized within epsilon(eps), skip this pair
if (np.abs(a2 - alph2) < eps * (a2 + alph2 + eps)):
return 0, model
a1 = alph1 + s * (alph2 - a2) #根据新 a2计算新 a1 Equation(J18)
b1 = E1 + y1*(a1 - alph1) * k11 + y2 * (a2 - alph2) * k12 + model.b #更新截距b的值 Equation (J20)
b2 = E2 + y1*(a1 - alph1) * k12 + y2 * (a2 - alph2) * k22 + model.b #equation (J21)
# Set new threshoold based on if a1 or a2 is bound by L and/or H
if 0 < a1 and a1 < C:
b_new =b1
elif 0 < a2 and a2 < C:
b_new = b2
#Average thresholds if both are bound
else:
b_new = (b1 + b2) * 0.5
#update model threshold
model.b = b_new
# 当所训练模型为线性核函数时
#Equation (J22) 计算w的值
if model.user_linear_optim:
model.w = model.w + y1 * (a1 - alph1)*model.X[i1] + y2 * (a2 - alph2) * model.X[i2]
#在alphas矩阵中分别更新a1, a2的值
#Update model object with new alphas & threshold
model.alphas[i1] = a1
model.alphas[i2] = a2
#优化完成，更新差值矩阵的对应值
#同时更新差值矩阵其它值
model.errors[i1] = 0
model.errors[i2] = 0
#更新差值 Equation (12)
for i in range(model.m):
if 0 < model.alphas[i] < model.C:
model.errors[i] += y1*(a1 - alph1)*model.kernel(model.X[i1],model.X[i]) + \
y2*(a2 - alph2)*model.kernel(model.X[i2], model.X[i]) + model.b - b_new
return 1, model

def get_error(model, i1):
if 0< model.alphas[i1] <model.C:
return model.errors[i1]
else:
return decision_function_output(model,i1) - model.y[i1]



def examine_example(i2, model):
y2 = model.y[i2]
alph2 = model.alphas[i2]
E2 = get_error(model, i2)
r2 = E2 * y2
#重点：这一段的重点在于确定 alpha1, 也就是old a1，并送到take_step去analytically 优化
# 下面条件之一满足，进入if开始找第二个alpha，送到take_step进行优化
if ((r2 < -tol and alph2 < model.C) or (r2 > tol and alph2 > 0)):
if len(model.alphas[(model.alphas != 0) & (model.alphas != model.C)]) > 1:#筛选器
#选择Ei矩阵中差值最大的先进性优化
# 要想|E1-E2|最大，只需要在E2为正时，选择最小的Ei作为E1
# 在E2为负时选择最大的Ei作为E1
if model.errors[i2] > 0:
i1 = np.argmin(model.errors)
elif model.errors[i2] <= 0:
i1 = np.argmax(model.errors)
step_result,model = take_step(i1,i2, model)
if step_result:
return 1, model
# 循环所有非0 非C alphas值进行优化，随机选择起始点
for i1 in np.roll(np.where((model.alphas != 0) & (model.alphas != model.C))[0],
np.random.choice(np.arange(model.m))):
step_result, model = take_step(i1, i2, model)
if step_result:
return 1, model

#alpha2确定的情况下，如何选择alpha1? 循环所有(m-1) alphas, 随机选择起始点
for i1 in np.roll(np.arange(model.m), np.random.choice(np.arange(model.m))):
#print("what is the first i1",i1)
step_result, model = take_step(i1, i2, model)

if step_result:
return 1, model
#先看最上面的if语句，如果if条件不满足，说明KKT条件已满足，找其它样本进行优化，则执行下面这句，退出
return 0, model

#核心函数
def fit(model):

numChanged = 0 #numChanged存放优化返回的结果，如果优化成功，则返回1，反之为0
examineAll = 1 #examineAll表示从0号元素开始优化，如果所有都优化完成，则赋值为0
#loop num record
#计数器，记录优化时的循环次数
loopnum = 0
loopnum1 = 0
loopnum2 = 0
# 当numChanged = 0 and examineAll = 0时循环退出
# 实际是顺序地执行完所有的样本，也就是第一个if中的循环，
# 并且 else中的循环没有可优化的alpha，目标函数收敛了：在容差之内，并且满足KKT条件
# 则循环退出，如果执行2000次循环仍未收敛，也退出
# 重点：这段的重点在于确定 alpha2，也就是old a 2, 或者说alpha2的下标，old a2和old a1都是heuristically 选择
while(numChanged > 0) or (examineAll):
numChanged = 0
if loopnum == 2000:#设置循环次数
break
loopnum = loopnum + 1
if examineAll:
loopnum1 = loopnum1 + 1 # 记录顺序一个一个选择alpha2时的循环次数
# # 从0,1,2,3,...,m顺序选择a2的，送给examine_example选择alpha1，总共m(m-1)种选法
for i in range(model.alphas.shape[0]):
examine_result, model = examine_example(i, model)
numChanged += examine_result
else: #上面if里m(m-1)执行完的后执行
loopnum2 = loopnum2 + 1
# loop over examples where alphas are not already at their limits
for i in np.where((model.alphas != 0) & (model.alphas != model.C))[0]:#筛选器，用于筛选alpha
examine_result, model = examine_example(i, model)
numChanged += examine_result
if examineAll == 1:
examineAll = 0
elif numChanged == 0:
examineAll = 1
print("loopnum012",loopnum,":", loopnum1,":", loopnum2)
return model
# can be replaced as per different model u want to show

#产生非线性数据，曲线的
X_train, y = make_circles(n_samples=500, noise=0.2,factor=0.1,random_state=2)

#产生非线性数据，交叉的
#X_train,y = make_moons(n_samples = 500, noise=0.2,random_state =1)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train, y)
y=2*y-1

#print('X_train',':', X_train)
# print('y',':',y)

#Set model parameters and initial values
C = 1.0
m = len(X_train_scaled)
initial_alphas = np.zeros(m)
initial_b = 0.0

# Set tolerances
tol = 0.01 # error tolerance
eps = 0.01 # alpha tolerance

# 初始化smo结构，使用高斯核函数
model = SMOStruct(X_train_scaled, y, C, lambda x, y: gaussian_kernel(x,y,sigma=0.5),initial_alphas, initial_b, np.zeros(m), user_linear_optim=False)

#initialize error cache
#先把这个注释掉
initial_error = decision_function(model.alphas, model.y, model.kernel,
model.X, model.X, model.b) - model.y
model.errors = initial_error

print("开始拟合模型...")
#开始训练
output = fit(model)
#绘制训练完，找到分割平面的图
fig,ax = plt.subplots()
grid,ax = plot_decision_boundary(output, ax)

plt.savefig("squares3.png",
bbox_inches ="tight",
pad_inches = 1,
transparent = True,
facecolor ="w",
edgecolor ='w',
dpi=300,
orientation ='landscape')

输出结果：
开始拟合模型...
loopnum012 2000 : 12 : 1988

4、参考文献

[1]J. Platt, “Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines,” Technical Report MSR-TR-98-14, Microsoft Research, 1998.

需要J. Platt 论文的家人们可以去百度网盘（永久有效）获取：

链接：https://pan.baidu.com/s/1qAu4ueR_ucJO_WbOKAYg2w?pwd=7woc
提取码：7woc
--来自百度网盘超级会员V5的分享

更多优质内容持续发布中，请移步主页查看。

点赞+关注,下次不迷路！