题目：

链接：剑指 Offer 12. 矩阵中的路径；LeetCode 79. 单词搜索
难度：中等

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

例如，在下面的 3×4 的矩阵中包含单词 “ABCCED”（单词中的字母已标出）。

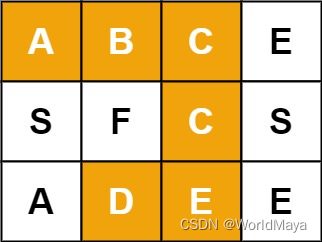
示例 1：

输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
输出：true

示例 2：

输入：board = [[“a”,“b”],[“c”,“d”]], word = “abcd”
输出：false

提示：

• m == board.length
• n = board[i].length
• 1 <= m, n <= 6
• 1 <= word.length <= 15
• board 和 word 仅由大小写英文字母组成

深度优先搜索：

简单的深搜。从单词的首字符开始在网格上逐字符逐方向的深搜，dfs函数传递的参数是当前网格中搜索的位置和当前单词中搜索的字符位置，单词全部匹配完成或者深搜所有路径都已搜索过即为完成。有一个visited数组记录访问过的位置、避免字符重复使用。
详细请看代码注释。

代码：

class Solution {
public:
    string Word;  // 查找的单词
    int len;  // 单词长度
    vector<vector<char>> Board;  // 网格
    int m, n;  // m * n 的网格
    vector<vector<bool>> visited;  // 单元格是否已被访问
    bool dfs(int i, int j, int k) {  // i,j 为当前网格位置，k为当前查找的word字符位置
        if(i < 0 || i >= m || j < 0 || j >= n) return false;  // 边界判断
        if(visited[i][j]) return false;  // 字符不可重复使用
        if(Board[i][j] == Word[k]) {  // 当前字符匹配成功
            visited[i][j] = true;
            if(k == len - 1) return true;  // 查找到单词终点，返回成功
            else {
                if(dfs(i - 1, j, k + 1)) return true;  // 没查找完成，继续在当前位上下左右四个方向查找下一个字符
                if(dfs(i + 1, j, k + 1)) return true;
                if(dfs(i, j - 1, k + 1)) return true;
                if(dfs(i, j + 1, k + 1)) return true;
                visited[i][j] = false;  // 下一字符匹配失败，释放当前访问位
            }
        }
        return false;  // 当前字符不匹配，或下一字符所有方向上都匹配失败，返回失败
    }
    bool exist(vector<vector<char>>& board, string word) {
        Board = board;
        m = board.size(), n = board[0].size();
        Word = word;
        len = word.size();
        visited.resize(m, vector<bool>(n, false));  // 访问数组初始化
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                bool flag;
                if(board[i][j] == word[0]) flag = dfs(i, j, 0);  // 从单词第一个字符开始搜索
                if(flag) return true;
            }
        }
        return false;
    }
};

时间复杂度：一个非常宽松的上界为O(M * N * 3^L),其中M,N为网格的长度与宽度，L为字符串word的长度。在每次调用函数dfs时，除了第一次可以进入4个分支以外，其余时间我们最多会进入3个分支（因为每个位置只能使用一次，所以走过来的分支没法走回去）。由于单词长为L，故dfs(i, j, 0)的时间复杂度为O(3^L)，而我们要执行O(M * N)次检查。然而，由于剪枝的存在，我们在遇到不匹配或已访问的字符时会提前退出，终止递归流程。因此，实际的时间复杂度会远远小于Θ(M * N * 3^L)。

空间复杂度：O(M * N)。我们额外开辟了O(M * N)的visited数组，同时栈的深度最大为O(min(L, M * N))。