1.摩尔定律(Moore's Law):集成电路上可以容纳的晶体管数目在大约每经过18个月到24个月便会增加一倍。换言之,处理器的性能大约每两年翻一倍,同时价格下降为之前的一半。。
2.登纳德缩放定律(Dennard Scaling):随着晶体管尺寸的缩小,其功率密度保持不变,从而使芯片功率与芯片面积成正比。
3.阿姆达尔定律(Amdahl’s Law):早在 1967 年,计算机体系结构领域的元老 Amdahl 提出的以他名字命名的定律,便已经向我们阐明了衡量处理器并行计算后效率提升能力的经验法则。其致力于并行处理系统的研究,对于固定负载情况下描述并行处理效果的加速比s,阿姆达尔经过深入研究给出了如下公式:S=1/((1-a)+a/n)
目录
一、摩尔定律(Moore's Law)
(1)主要内容
(2)发展前景
二、登纳德缩放定律(Dennard Scaling)
(1)主要内容
(2)发展前景
三、阿姆达尔定律(Amdahl’s Law)
(1)主要内容
(2)公式推导
2.1 Fraction enhanced
2.2 Speedup enhanced
2.3 带入 Amdahl's law
参考资料:
一、摩尔定律(Moore's Law)
(1)主要内容
1959年,美国著名半导体厂商仙童公司首先推出了平面型晶体管,紧接着于1961年又推出了平面型集成电路。这种平面型制造工艺是在研磨得很平的硅片上,采用一种所谓“光刻”技术来形成半导体电路的元器件,如二极管、三极管、电阻和电容等 。
只要“光刻”的精度不断提高,元器件的密度也会相应提高,从而具有极大的发展潜力。因此平面工艺被认为是“整个半导体的工业键”,也是摩尔定律问世的技术基础。
1965年时任仙童半导体公司研究开发实验室主任的摩尔应邀为《电子学》杂志35周年专刊写了一篇观察评论报告,题目是:“让集成电路填满更多的元件”。在摩尔开始绘制数据时,发现了一个惊人的趋势:每个新芯片大体上包含其前任两倍的容量,每个芯片的产生都是在前一个芯片产生后的18-24个月内 。如果这个趋势继续,计算能力相对于时间周期将呈指数式的上升。 Moore的观察资料,就是现在所谓的Moore定律。其所阐述的趋势一直延续至今,且仍不同寻常地准确 。人们还发现这不仅适用于对存储器芯片的描述,也精确地说明了处理机能力和磁盘驱动器存储容量的发展。该定律成为许多工业对于性能预测的基础 。在26年的时间里,芯片上的晶体管数量增加了3200多倍,从1971年推出的第一款4004的2300个增加到奔腾II处理器的750万个 。
归纳起来,“摩尔定律”主要有以下3种“版本”:
1、集成电路芯片上所集成的电路的数目,每隔18个月就翻一番;
2、微处理器的性能每隔18个月提高一倍,而价格下降一半;
3、用一美元所能买到的计算机性能,每隔18个月翻两番 。
以上几种说法中,以第一种说法最为普遍,第二、三两种说法涉及价格因素,其实质是一样的。三种说法虽然各有千秋,但在一点上是共同的,即“翻番”的周期都是18个月,至于“翻一番”(或两番)的是“集成电路芯片上所集成的电路的数目”或是整个“计算机的性能”,还是“一美元所能买到的性能”就见仁见智了。
(2)发展前景
摩尔定律问世已40多年,人们不无惊奇地看到半导体芯片制造工艺水平以一种令人目眩的速度提高。Intel的微处理器芯片Pentium4的主频已高达2GHz,2011年推出了含有10亿个晶体管、每秒可执行1千亿条指令的芯片。这种发展速度是否会无止境地持续下去是成为人们所思考的问题 。
晶体管更小密度更高的好处:
- 晶体管越小,要移动的电荷量就越小,能更快切换状态,耗电更少。
- 电路更紧凑,还意味着信号延迟更低,导致时钟速度更快。
进一步做小,会面临2个大问题:
- 用光掩膜把图案弄到晶圆上,因为光的波长,精度已达到极限。所以科学家在研制波长更短的光源,投射更小的形状。
- 当晶体管非常小,电极之间可能只距离几个原子,电子会跳过间隙,这叫:量子隧道效应。如果晶体管漏电,就不是好开关,科学家和工程师在努力找解决办法,实验室中已造出小至1纳米的晶体管,能不能商业量产仍然未知,未来也许能解决。
从技术的角度看,随着硅片上线路密度的增加,其复杂性和差错率也将呈指数增长,同时也使全面而彻底的芯片测试几乎成为不可能。一旦芯片上线条的宽度达到纳米(10^-9米)数量级时,相当于只有几个分子的大小,这种情况下材料的物理、化学性能将发生质的变化,致使采用现行工艺的半导体器件不能正常工作,摩尔定律也就要走到尽头。斯坦福大学名誉校长、谷歌董事长兼MIPS计算机系统创始人John Hennessy说:“‘摩尔定律’它不是法则,而是一个志向,是一个目标。是值得一试的东西。”他说到:“它肯定在放缓,但要说‘摩尔定律’已死还为时过早。”
物理学家加来道雄(Michio Kaku)是纽约城市大学一名理论物理学教授,他表示导致摩尔定律失效的两大主因是高温和漏电。这也正是硅材料寿命终结的原因。加来道雄表示这与科学家们最初预测摩尔定律没落大相径庭。科学家应该能继续挖掘硅部件的潜力,从而在未来几年时间里维持摩尔定律的生命力;但在3D芯片等技术也都耗尽潜力以后,那么也就将达到极限 。
基于摩尔定律的这种情况,业界提出了“More-Than-Moore”(简称MTM,即“超越摩尔定律”),试图从更多的途径来维护摩尔定律的发展趋势,并且从摩尔定律的“更多更快”,发展到MTM的“更好更全面”。摩尔定律在Logic类和Memory类的集成电路的发展中提出和得到验证,而MTM则适用于更多类型的集成电路,如Analog、RF、Image Sensor、Embedded DRAM、Embedded FLASH、MEMS、High Voltage等,通过改变基础的晶体管结构(SOI、FIN-FET),各类型电路兼容工艺,先进封装(晶圆级封装、SiP、3D多芯片封装)等技术,使一个系统级芯片能支持越来越多的功能,同样可以降低芯片的成本、提高电路的等效集成度 。
(8条消息) 傻白入门芯片设计,先进封装技术(五)_好啊啊啊啊的博客-CSDN博客
然而目前最担忧的问题不是摩尔定律的放缓,真正的问题在于Dennard Scaling定律的失效。
二、登纳德缩放定律(Dennard Scaling)
(1)主要内容
Dennard缩放定律是1974年Dennard提出,与大名鼎鼎的摩尔定律一起统治了集成电路很多年。
Dennard提出,晶体管的尺寸在每一代技术中都缩小了30% (0.7倍),因此它们的面积A减少了50%。这意味着电路减少了30% (0.7倍)的延迟,因此增加了约40% (1.4倍)的工作频率。最后,为了保持电场恒定,电压降低了30%,能量降低了65%,功率降低了50%。因此,在每一代技术中,晶体管密度增加一倍,电路速度提高40%,功耗(晶体管数量增加一倍)保持不变。
Dennard Scaling 预测随着晶体管密度的增加,每个晶体管的能耗将降低,因此硅芯片上每平方毫米上的能耗几乎保持恒定。由于每平方毫米硅芯片的计算能力随着技术的迭代而不断增强,计算机将变得更加节能。
然而,自2005-2007年前后,Dennard缩放比例定律似乎已经失效。截至2016年,集成电路中的晶体管数量仍在跟随“摩尔定律”增加,但由此带来的性能改善却更为缓慢。这种情况的主要原因是在芯片尺寸不变,晶体管数量变多的情况下,电流泄漏会带来更大的挑战,也会导致芯片升温,从而造成热失控的威胁,从而进一步增加能源成本。
(2)发展前景
1986 年至 2002 年间,指令级并行(ILP)是提高性能的主要架构方法。而且随着晶体管速度的提高,其性能每年能提高 50% 左右。登纳德缩放定律的终结意味着工程师必须找到更加高效的并行化利用方法。
为了保持工作流程完整,需要预测分支,并根据推测将代码放入工作流程中以便执行。推测的使用是 ILP 高性能和芯片低能效的源头所在。如果分支预测完美,推测就能提高 ILP 性能,但能耗会增加一些——甚至可能节约能耗——但如果分支预测出现失误,处理器就必须抛弃错误的推测指令,其计算工作及所耗能量就会付之东流。处理器的内部状态也必须恢复到错误预测分支之前的状态,这将花费额外的时间和能量。很少有通用程序能够如此准确地预测分支。架构师需要一种不同的方法来实现性能改进,于是多核时代就这样诞生了。多核将识别并行性和决定如何利用并行性的责任转移给程序员和语言系统。
Dennard缩放比例定律的失效以及由此导致的无法显著提高时钟频率,已经导致大多数CPU制造商将重点放在多核处理器上,以此作为提高性能的一种替代方法。
增加内核数量有利于提高(虽然并非完全)工作负载,但是由于拥有多个核心而增加的活动开关元件仍然会导致整体功耗增加,从而加剧CPU功耗问题。最终的结果是,在不违反功率约束的情况下,一个集成电路中只有一小部分能够在一定时间处于实际有效状态,其余的(不活跃的)区域称为暗硅。多核并不能解决由登纳德缩放定律终结带来的能效计算挑战。每个活跃的核都会消耗能量,无论其对计算是否具有有效贡献。一个主要的障碍可以用阿姆达尔定律(Amdahl's Law)表述。
三、阿姆达尔定律(Amdahl’s Law)
(1)主要内容
Amdahl加速定律的基本出发点是:1.对于很多科学计算,实时性要求很高,即在此类应用中时间是个关键因素,而计算负载是固定不变的。为此在一定的计算负载下,为达到实时性可利用增加处理器数来提高计算速度;2.因为固定的计算负载是可分布在多个处理器上的,这样增加了处理器就加快了执行速度,从而达到了加速的目的。在此意义下,1967年Amdahl推导出了固定负载的加速公式。
阿姆达尔定律是计算机系统设计的重要定量原理之一,于1967年由IBM360系列机的主要设计者阿姆达尔首先提出。该定律是指:系统中对某一部件采用更快执行方式所能获得的系统性能改进程度,取决于这种执行方式被使用的频率,或所占总执行时间的比例。阿姆达尔定律实际上定义了采取增强(加速)某部分功能处理的措施后可获得的性能改进或执行时间的加速比。简单来说是通过更快的处理器来获得加速是由慢的系统组件所限制。
阿姆达尔曾致力于并行处理系统的研究。对于固定负载情况下描述并行处理效果的加速比s,阿姆达尔经过深入研究给出了如下公式:
S为 speedup,代表全局加速倍速(原来总时间/ 加速后总时间),a 为并行计算所占比例(可以并行计算代码量 / 总代码量), n为并行节点处理个数,可以理解为 CPU 的核心数,这里先简要介绍下,后面会详细说明并且推导。
(2)公式推导
2.1 Fraction enhanced
Fraction enhanced 顾名思义是部分提高。例如我的程序总共有 100 行代码,其中 50 行是可以通过并行计算的,那么这 50 行代码就是 Fraction enhanced 。但是实际上 Fraction enhanced 是一个比例数值,是并行计算代码 / 总代码量。
例如上面的例子, Fraction enhanced = 50/100 = 0.5 ,由此我们可以发现, Fraction enhanced 的值永远小于 1。
2.2 Speedup enhanced
如上面公式所得,Speedup enhanced 等于 原有运行时间 / 并行计算加速后的时间 。例如系统原来串行计算需要 6 秒,加速后只需要 3 秒,那么 Speedup enhanced = 6/3 = 2 。由此可知 Speedup enhanced 的值永远大于 1。
2.3 带入 Amdahl's law
我们分别把 Fraction enhanced 和 Speedup enhanced 带入 Amdahl's law。Fraction enhanced 对应公式中的 ,即并行计算所占比例。Speedup enhanced 对应 ,即并行节点处理个数。
Speedup enhanced 为什么可以代替 ?
这里大家可能有一点疑问,Speedup enhanced 明明是 未加速前时间 / 加速后的时间,为什么就可以代表并行节点处理个数。在理论上,单核处理器处理一个任务需要 100 秒,那么双核处理它应该需要 50 秒。时间上它提速了 2 倍, cpu 个数上它也提升了 2 倍,故两个可以替换。
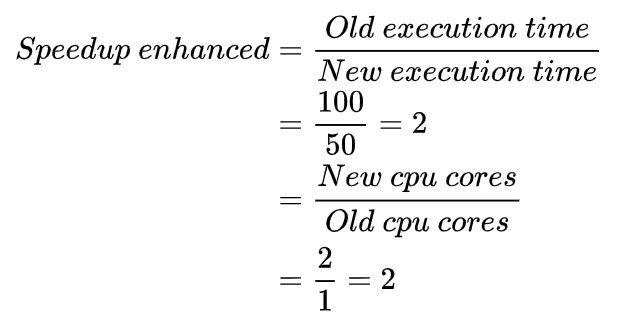
带入公式后得:

将已知参数带入公式:


带入公式后得:

综上,让我们回到最初的公式:
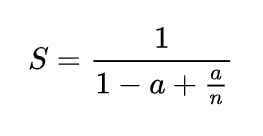
为并行计算所占比例, 为并行节点处理个数。当 时(即只有串行没有并行),无论 为多少,加速比 均为 1。当 ,当 cpu 核心数无限增多的时候,极限加速比 。例如若并行代码有 75%,极限加速比不能超出 4。由此我们可知,在并行系统中一味的增加运算资源,并不能永远成倍的提升系统整体性能。
参考资料:
Amdahl's law(阿姆达尔定律)公式推导与思考 - 简书 (jianshu.com)
(8条消息) 集成电路(IC)&摩尔定律_npc_blog的博客-CSDN博客_集成电路摩尔定律
计算机体系架构未来趋势(深度)-技术圈 (proginn.com)
(8条消息) Dennard scaling(MOSEFT scaling)_bentty_lee的博客-CSDN博客_dennard scaling
晶体管变小之后,Dennard定律更值得关注,散热和功耗推动专业化 (baidu.com)
三大基本定律失效,EDA公司正在提出新的芯片设计思路 (baidu.com)




![[第二十二篇]——Docker 安装 MongoDB](https://img-blog.csdnimg.cn/img_convert/53ddec9b43ef36c3d6fe140664ac2c58.png)