在Shader的学习中，我们可能需要一些数学知识，我也是学习了一段时间，之前数学的知识都忘了，重新来一遍吧，我把学习的点分享一下。

向量：

点乘：
向量A·向量B = A向量的模 * B向量的模 * cosθ
一般用来计算向量夹角cosθ，这里可以看下Lambert （兰伯特）光照模型这篇文章来感受下在Shader中的向量计算

叉乘： 计算两个向量构成平面的法向量

矩阵：

矩阵相乘必须要满足一个规则：第一个矩阵的列数要与第二个矩阵的行数相同。
而得到的结果一定为：行数为第一个矩阵的行数，列数为第二个矩阵的列数。
一个m行n列的向量A与一个n行r列的向量B相乘，得到m行r列的向量C。

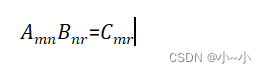
例如矩阵A的维度是3×2，矩阵B的维度是2×4，那么AB的维度就是3×4。如下

另外还有一个计算技巧：
C23的值是从哪计算得来呢？可以看C23的下标，是由第一个矩阵的第2行 乘以 第二个矩阵的第3列得来

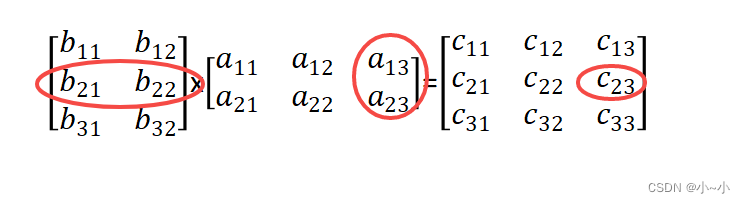
矩阵乘法的一些性质

• 性质一：矩阵乘法不满足交换律。
  也就是说，通常情况下：AB≠BA
• 性质二：矩阵乘法满足结合律。
  (AB)C=A(BC)
  矩阵乘法的结合律可以扩展到更多矩阵的相乘。例如，ABCD=((A(BC))D)=(AB)(CD)

向量与矩阵相乘

一个向量可以用（x,y,z）表示，现在我们让向量与矩阵相乘。
行向量与矩阵相乘：

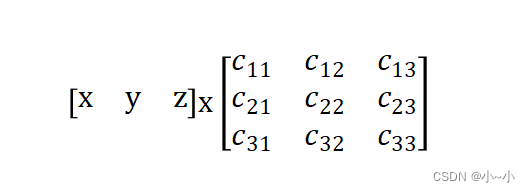
列向量与矩阵相乘

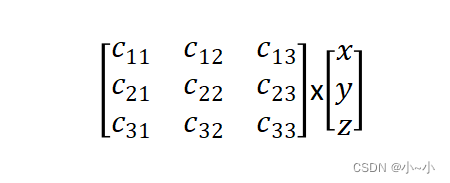
注意：在Unity中，矩阵与向量运算，通常采用列向量右乘

特殊的矩阵

1、方块矩阵

简称方阵，是指那些行和列数目相等的矩阵。在三维渲染里，最常使用的就是3×3和4×4的方阵

2、单位矩阵

一个特殊的对角矩阵是单位矩阵（identity matrix），任何矩阵与它相乘还是原来的矩阵。

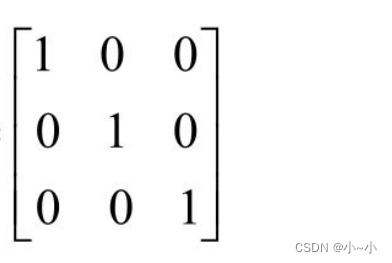
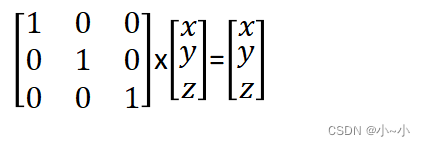
3、转置矩阵

直接举例：如下图

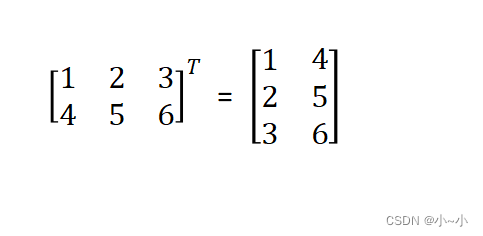
4、逆矩阵

不是所有的矩阵都有逆矩阵，该矩阵必须是个方阵。
逆矩阵几何意义：我们可以通过一个矩阵表示一个变换，如何把矩阵还原呢？可以使用逆矩阵来还原这个变换。
例如：

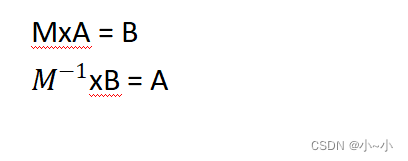
矩阵变换

线性变换：

满足下面条件的可以称之为线性变换

 f(x)+f(y)=f(x+y)
 kf(x)=f(kx)

在 Unity 中，旋转、缩放为线性变换
对于线性变换来说，对一个三维的矢量进行变换，使用3×3的矩阵就可以表示所有的线性变换

非线性变换：

当然是不满足上面条件了，平移变换属于非线性变换
而对于非线性变换，3x3的矩阵已无法满足，既然三维空间无法满足，那么我用更高纬度的空间，4维空间来实现非线性变换。
使用4x4的矩阵来做非线性变换，我们称之为仿射变换（affine transform）。
把原来的三维矢量转换成四维矢量，这就是我们所说的齐次坐标（homogeneous coordinate）。
齐次坐标：

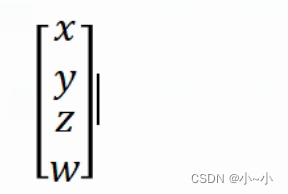
对于一个点w 补1，因为点会受到平移变换的影响
对应一个方向向量 w 补0，因为向量不会受平移的影响，不管怎么平移向量是不会变的。

平移矩阵变换。

下面我们来实现平移矩阵变换，来感受一下

假设现在有一个点为(1,2,4)，把该点平移（2,1,3）,最后的结果是(3,3,7)，那么通过矩阵是怎么运算的呢？我们使用齐次坐标空间，由于此处是点的平移那么 w 处补0

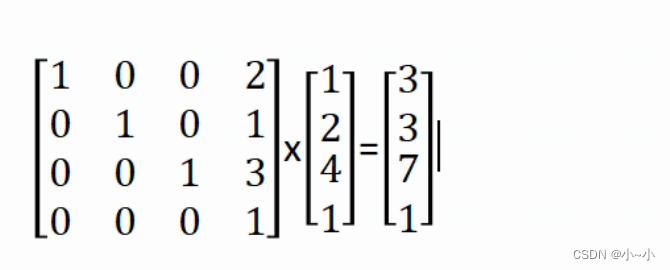
如果现在改为方向向量(1,2,4)，平移后方向向量是不变的，还是（1，2，4），此处w补0

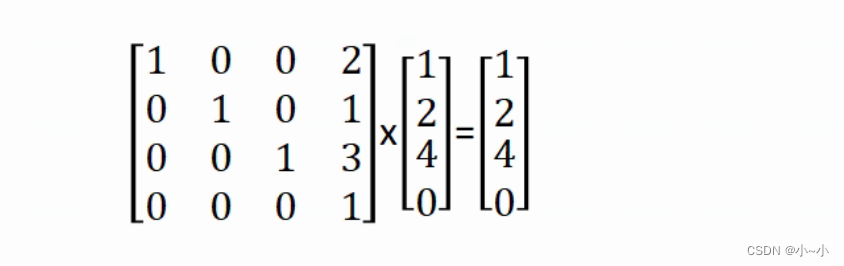
缩放矩阵

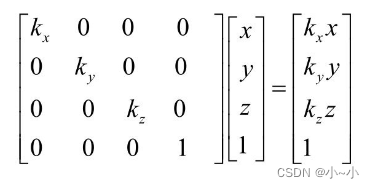
旋转矩阵

沿x轴旋转

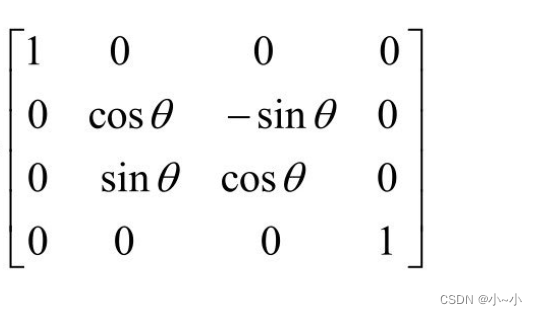
沿y轴旋转

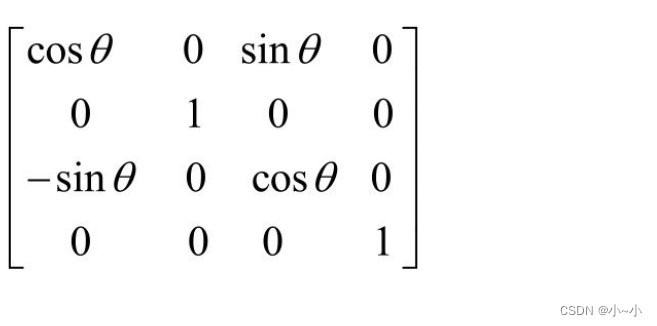
沿z轴旋转

复合变换举例

我们把上面的平移缩放旋转来进行复合变换，说的再多，举一个例子可能更直观点。
点A（2,3,4）,绕z轴旋转30度，缩放（1，2，3），平移（6，7，8），我们用矩阵来计算下

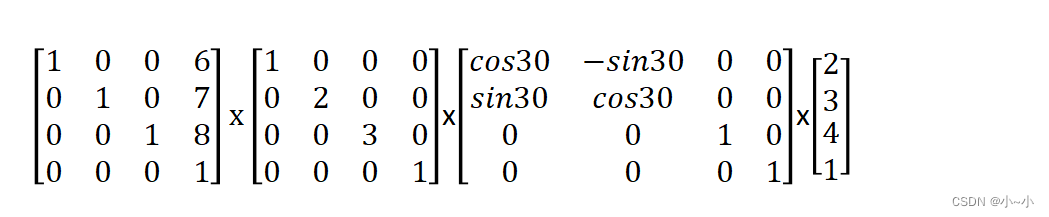
矩阵从右往乘，先旋转，再缩放，再平移。由于矩阵相乘满足结合律，我们可以把前面的三个矩阵相乘后得到一个变换矩阵，再于坐标点相乘

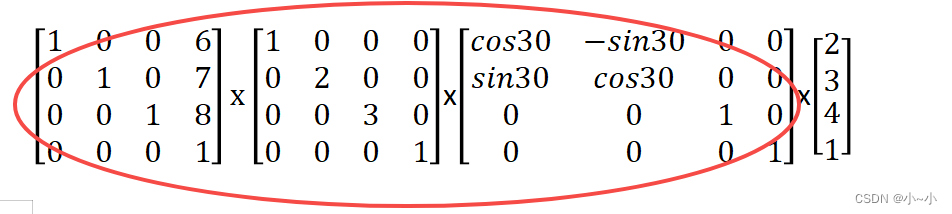
实际应用

在这里我们可以看Unity Shader的一个例子：
在Unity中需要一系列的矩阵变换才能被看到，我们来看看Unity的空间变换。

坐标空间

• 模型空间：物体的原始数据存储在模型空间下，点是相对于模型空间。
  当一个模型导入到Unity中后，我们可以在顶点着色器中访问到模型的顶点信息，其中包含了每个顶点的坐标。这些坐标都是相对于模型空间中的原点（通常位于模型的重心）定义的。
  在模型空间下我们看不到物体，我们需要把物体先转换到世界空间

• 世界空间：游戏运行时，把物体加载到场景中，会把点转换到世界空间下

• 观察空间：摄像机空间，观察空间的原点在摄像机处，把世界空间下的点转换到摄像机的视角空间下。

• 裁剪空间：到了观察空间，我们依然无法正常显示物体，需要进行下一步变换到裁剪空间，把摄像机外的物体裁剪掉，只有位于摄像机内的物体才会显示。

• 屏幕空间：在完成上面的操作后，我们需要把点投影到屏幕上，而屏幕时二维空间的显示器，把点投影到屏幕空间中，计算屏幕坐标，显示器才能正常显示。

Shader中相对于的矩阵

1:模型空间 2:世界空间 3:观察空间 4:裁剪空间

• UNITY_MATRIX_M：从模型空间，转换到世界空间
• UNITY_MATRIX_V：从世界空间，转换到观察空间
• UNITY_MATRIX_P：从观察空间，转换到裁剪空间
• UNITY_MATRIX_MV：从模型空间，到观察空间
• UNITY_MATRIX_VP：从世界空间，到裁剪空间
• UNITY_MATRIX_MVP：从模型空间，转换到裁剪空间

直接上图，看的比较清楚

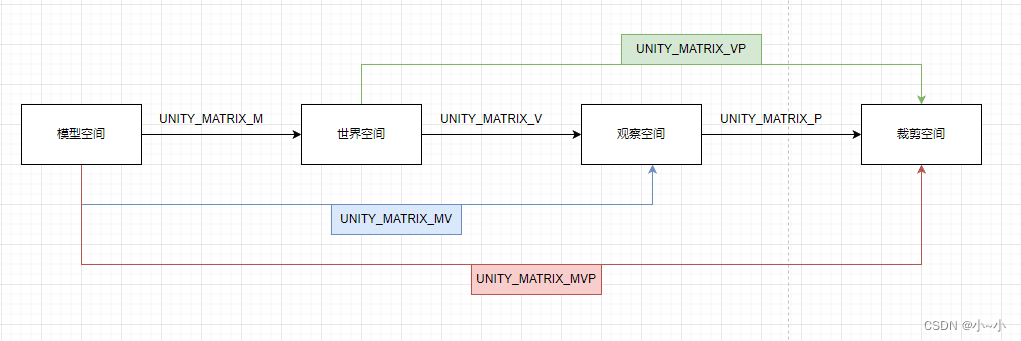
在顶点着色器中，需要对顶点进行空间变换。假如模型空间下的点A=(2,2,3)，向量可以用列矩阵表示。需要把该点转为世界空间下的点，再转为视图空间（我理解的是摄像机的空间），再转为裁剪空间。
UNITY_MATRIX_M x A = 世界空间下的坐标
UNITY_MATRIX_V x 世界空间下的坐标 = 观察空间下的坐标
UNITY_MATRIX_P x 观察空间下的坐标 = 裁剪空间下的坐标

由于矩阵时满足结合律的，上面的空间变换我们可以用一个矩阵来表示UNITY_MATRIX_MVP，UNITY_MATRIX_MVP x A把该点从模型空间转为世界空间

`mul(UNITY_MATRIX_MVP,A)`

在Unity中提供了相应的方法UnityObjectToClipPos，来进行坐标变换

    float4 vert(float4 v:POSITION):SV_POSITION{
                  return UnityObjectToClipPos(v);
                }

一个简单的Shader代码

Shader "My/01 shader"{
         Properties{
 
         }
        SubShader{
            Pass{
                CGPROGRAM

                #pragma vertex vert
                #pragma fragment frag
 				  #include "UnityCG.cginc"
                float4 vert(float4 v:POSITION):SV_POSITION{
                  return UnityObjectToClipPos(v);
                }

                fixed4 frag():SV_Target{
                    return fixed4 (1,1,1,1);
                }
                ENDCG
                }
        }
          FallBack  "Diffuse"
    
    }