如何理解分治算法？

分治算法（divide and conquer）的核心思想其实是，分而治之，也就是将原问题划分成n个规模较小，并且结构与原问题相似的子问题，递归第解决这些子问题，然后再合并其结果，就得到原问题的解。分治算法是一种处理问题的思想，递归是一种编程技巧。

分治算法3操作

分解：将原问题分解成一系列子问题；

解决：递归地求解各个子问题，若子问题足够小，则直接求解；

合并：将子问题的结果合并成原问题。

分治算法能解决的问题，一般需要满足的条件

原问题与分解的小问题具有相同的模式；

原问题分解成的小问题可以独立求解，子问题之间没有相关性；

具有分解终止条件，即，当问题足够小时，可以直接求解；

可以将子问题合并成原问题，并且合并的复杂度不高。

分治算法应用举例分析

假设有n个数据，期望数据从小到大排序，那完全有序的数据的有序度就是n*(n-1)/2，逆序度等于0；相反倒序排列的数据的有序度就是0，逆序度是n*(n-1)/2。

如何编程求出一组数据的有序对个数或逆有序对个数？

套用分治的思想来求数组A的逆序对个数。可以将数组分成前后两半A1和A2，分别计算A1和A2的逆序对个数K1和K2，然后再计算A1和A2之间的逆序对个数K3。那数组A的逆序对个数就等于K1+K2+K3。

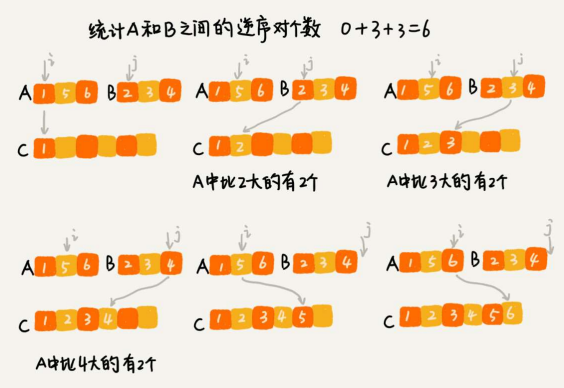
归并排序，就是将两个有序的小数组，合并成一个有序的数组。在这个合并的过程中，就可以计算这两个小数组的逆序对个数了。每次合并操作，都计算逆序对个数，把这个计算出来的逆序对个数求和，就是这个数组的逆序对个数了。

private int num = 0; // 全局变量或者成员变量

public int count(int[] a, int n) {
    num = 0;
    mergeSortCounting(a, 0, n-1);
    return num;
}

private void mergeSortCounting(int[] a, int p, int r) {
    if (p >= r) return;
    int q = (p+r)/2;
    mergeSortCounting(a, p, q);
    mergeSortCounting(a, q+1, r);
    merge(a, p, q, r);
}

private void merge(int[] a, int p, int q, int r) {
    int i = p, j = q+1, k = 0;
    int[] tmp = new int[r-p+1];
    while(i <= q && j <= r) {
        if (a[i] <= a[j]) {
            tmp[k++] = a[i++];
        } else {
            num += (q-i+1); //统计p-q之间，比a[j]大的元素个数
            tmp[k++] = a[j++];
        }
    }
    
    while(i <= q) { // 处理剩下的
        tmp[k++] = a[i++];
    }
    
    while(j <= r) {
        tmp[k++] = a[j++];
    }
    
    for (i=0; i<=r-p; ++i) {// 从tmp拷贝回a
        a[p+i] = tmp[i];
    }

}