帕克变换的物理意义

前面说到克拉克变换的物理意义，是将三相定子线圈产生磁场的过程，等效为2个正交放置的线圈，来产生同样的磁场。通过控制这两个正交线圈即可等效控制三相定子线圈。

还有一个问题，定子线圈产生的磁场，如果与转子位置不匹配就成了开环控制了，显然我们需要与转子的位置对应起来控制，这个过程也叫闭环控制。也就是不断的读取转子的位置，并根据这个位置，实时的给出当前所需要驱动磁场方向和强度。

定子磁场坐标是一定的，也就是我们之前说到的定子坐标系，和Ia-Iβ坐标系。
而转子的磁场是一直在旋转，这个叫转子坐标系。以转子自身来说，它的磁场是恒定的，只是旋转角度不停的在变化，我们也可以由此建立一个dq坐标系，如下

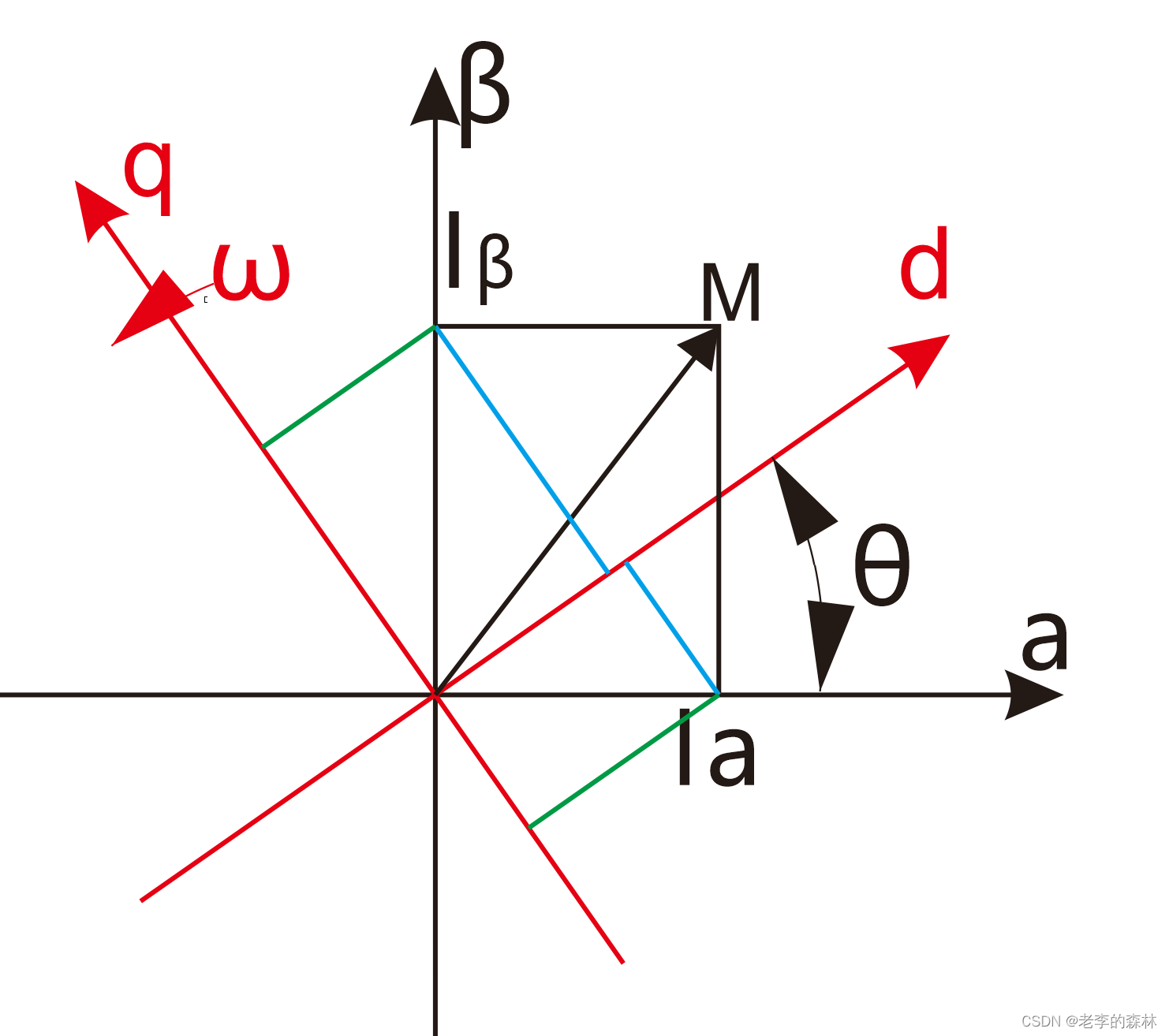
转子的横轴是d轴，也叫直轴，纵轴是q轴，也就是正交的意思，叫交轴。似乎是直轴表示的励磁电流，交轴表示的旋转的驱动力，不知道这样理解对不对。

d-q坐标系与a-β坐标系之间有一个θ角，这个代表的是转子旋转的角度。还有一个ω表示转子的旋转角速度。
在a-β坐标系内，有一个黑色的向量M，代表的是转子的磁场向量。也有一个ω表示磁场向量的旋转角速度，这两个ω是相同的含义。
这个M向量在a-β坐标系内是不停旋转的，但是在d-q坐标系内是不变的，在d-q坐标系内，它是Vd和Vq，是定值。只是相对于a-β坐标系来说，d-q坐标系是在不停的旋转而已。
如此我们就可以把电机的三个坐标系对应起来了，电机本身的坐标系是二维三轴坐标系，与a-β坐标系通过克拉克变换重合，就略去不画了。
θ角也叫电角度，它可以通过编码器来实时获得，电角度 = 编码器角度 * 极对数

帕克变换

M在a-β坐标系内的投影分别是ia和iβ，然后为了方便观看，把上面的图旋转一下，以d-q坐标系的视角来看，就是下图

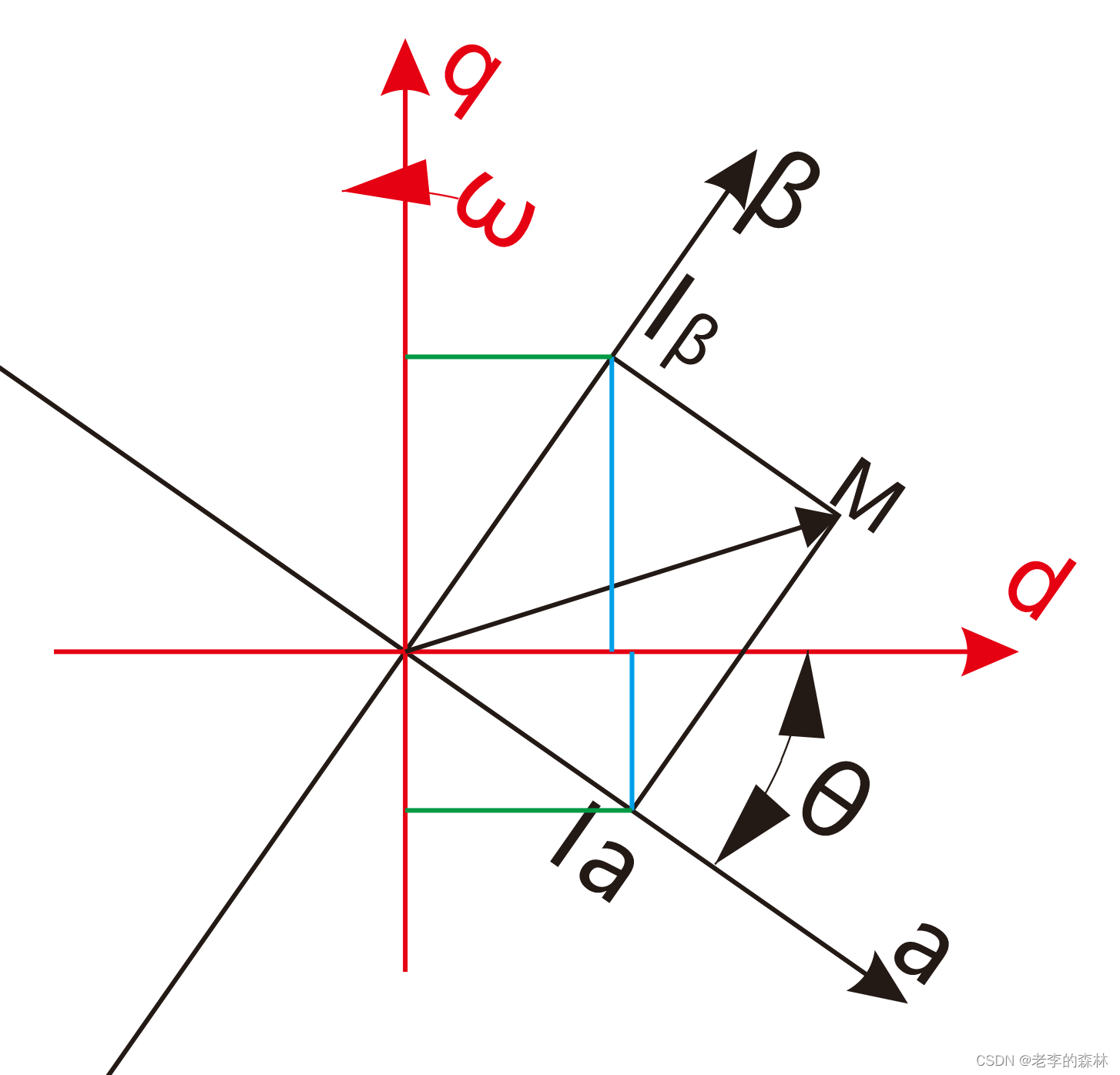
ia和iβ在d轴上的投影是两段绿色的线，都在id的正方向
ia和iβ在q轴上的投影是两段蓝色的线，ia在q轴的负方向，iβ在q轴的正方向。

用三角函数表示出来就是
id = iacosθ + iβsinθ
iq = -iasinθ + iβcosθ

写成矩阵就是

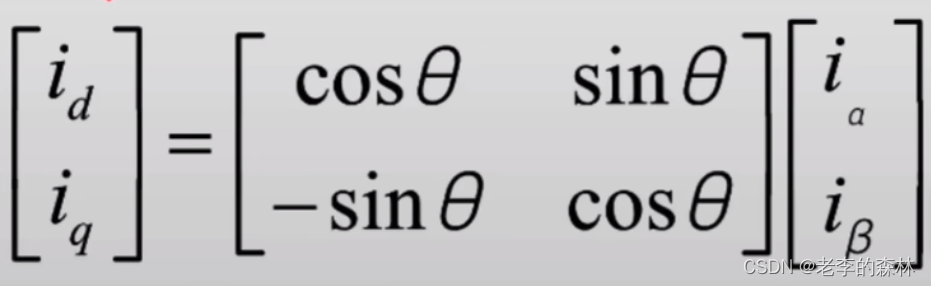
帕克逆变换

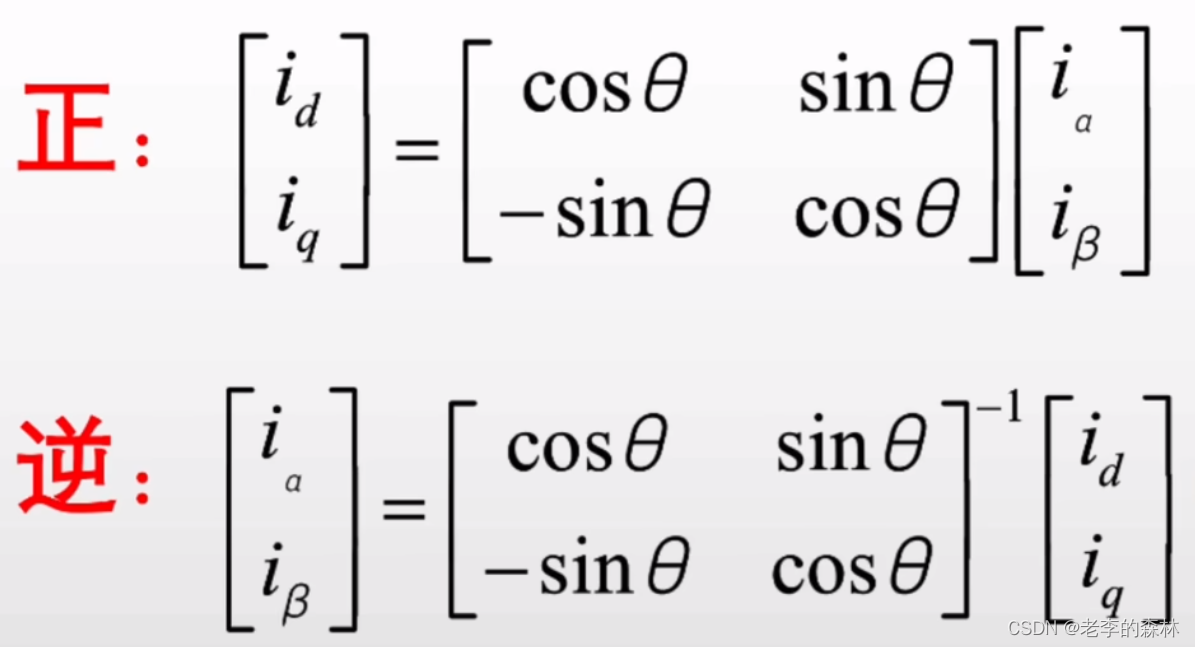
三角函数表示如下
ia = idcosθ - iqsinθ
iβ = idsinθ + iqcosθ

FOC方式驱动无刷电机所用到的数学知识就是克拉克变换和帕克变换，及其逆变换。

这两个变换是如此精妙，也如此简单，令人叹为观止。每当我读到这些人类智慧之光时，总是会被前人的智慧，以及他（她）们为推动人类科技进步所作的努力所感动，因为我也是做的技术这一行，自然明白这些成果得来之不易。在此向前辈们致敬！