D. Big Brush

https://codeforces.com/contest/1638/problem/D

题目描述

给你一张 $n\times m$ 大的网格纸，你有一把 $2\times 2$ 的刷子，每次只能涂满这么多，即 $(i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)$，每个格子都需要涂上颜色，颜色一共有不超过 $n\times m$ 种，一个格子可以被涂多次，但是以最后一次为准。

现在给你一个像这样涂好的网格纸，你需要求出上色的步骤。

输入描述

输入的第一行包含两个整数 n 和 m (2≤n,m≤1000) — 画布的尺寸。

在接下来的 n 行输入中的第 i 行，将有 m 个整数。其中第 j 个是 ai,j (1≤ai,j≤nm) — 细胞 (i,j) 的颜色。

输出描述

如果没有解决方案，则打印一个整数 -1。

否则，在第一行打印一个整数 q (1≤q≤nm) — 操作数。

接下来，按顺序打印操作。在接下来的 q 行的第 k 行，打印三个整数 i, j, c (1≤i<n, 1≤j<m, 1≤c≤nm) — 第 k 次操作的描述。

如果有多个解决方案，请打印任何一个。

样例

#1

4 4
5 5 3 3
1 1 5 3
2 2 5 4
2 2 4 4

6
1 3 3
3 3 4
2 2 5
1 1 5
2 1 1
3 1 2

3 4
1 1 1 1
2 2 3 1
2 2 1 1

-1

提示

在第一个测试用例中，解决方案不是唯一的。这是其中之一：

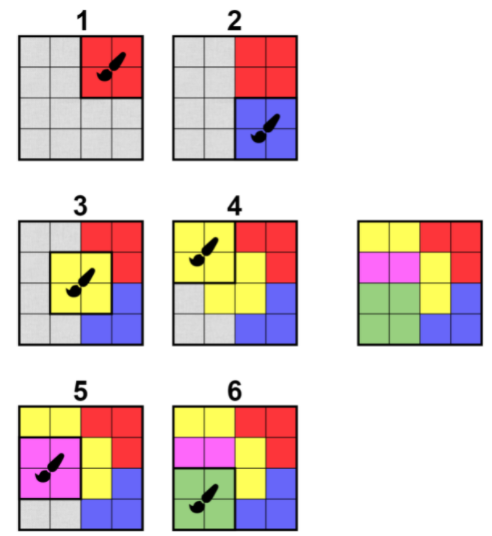
在第二个测试案例中，没有办法获得给定的绘画，因此答案是 -1。

解析

让我们头疼的是无法确定一个格子到底应该填什么色，因为后面的上色步骤或许会覆盖它。

那会存在一个确定的色块吗？答案是肯定的，当我们最后一次上色时，给最后一个点 $(i,j)$ 上色，

则 $(i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)$ 都是同一个颜色，也就是说，无论前面的如何操作，这个色块无论是什么颜色，在最后一步的时候都会被填充为同一色块，换句话说，这几个色块可以与任意颜色匹配，因为到了最后一步都会被填充回来，每次找到这种色块，我们需要将其设置为 “-1”，这种色块我们称之为“万能块”。

那我们就要逆着来看，先找到所有的万能块，以此为最后一步，找找周围的格子是否也存在万能块，包括自己在内共可以找到 9 种万能块：

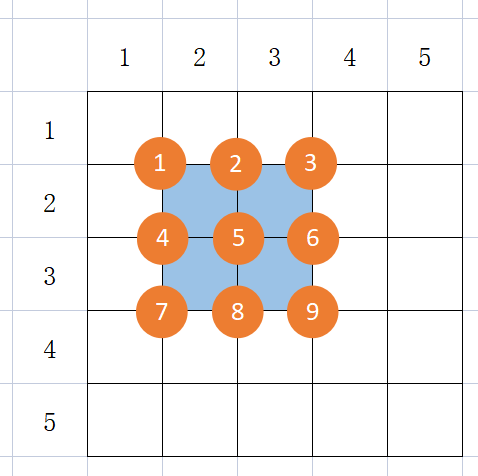
每次找到一个万能块就入队列，然后 BFS 进行找，一直到开始位置（我们是逆序的）位置，最后在正序输出即可。

我们从最后一步开始往前推进，将所有万能块设置为 -1，一直到最后若全盘为 -1，即有解，否则无解。

AC Code

public class Main {
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static StreamTokenizer st = new StreamTokenizer(br);
    static PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));

    static int[] dx = {0, 1, 0, 1}; // dx,dy 是刷子，表示 4 个格子的移动坐标
    static int[] dy = {0, 0, 1, 1};
    static int[][] board = null; // 网格纸
    static int n, m;
    static Deque<Node> ans = new LinkedList<>(); // 存储答案，最后要倒序输出

    public static void main(String[] args) throws Exception {
        n = nextInt(); m = nextInt();
        board = new int[n+1][m+1];
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= m; j++) board[i][j] = nextInt();
        bfs();
        out.flush();
    }

    public static void bfs() {
        Deque<Node> queue = new LinkedList<>();
        // 预先将所有的万能块入队列
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= m; j++) {
                int flag = check(i, j);
                if(flag != -1) {
                    queue.push(new Node(i, j, flag));
                    ans.addLast(new Node(i, j, flag));
                    color(i, j);
                }
            }
        }

        while(!queue.isEmpty()) {
            Node node = queue.removeFirst();
            for(int i = node.x - 1; i <= node.x + 1; i++) {
                for(int j = node.y - 1; j <= node.y + 1; j++) {
                    int flag = check(i, j);
                    if(flag != -1) {
                        queue.push(new Node(i, j, flag));
                        ans.addLast(new Node(i, j, flag));
                        color(i, j);
                    }
                }
            }
        }

        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= m; j++) {
                if(board[i][j] != -1) {
                    System.out.println("-1");
                    return;
                }
            }
        }

        System.out.println(ans.size()); // 步骤
        while(!ans.isEmpty()) {
            Node last = ans.pollLast();
            out.println(last.x + " " + last.y + " " + last.k);
        }
    }

    // 验证以 (x,y) 为起点的四个格子是否为万能块，true 就返回该万能块颜色
    public static int check(int x, int y) {
        HashSet<Integer> set = new HashSet<>(); // 借助 set 的不重复的特性来存储元素
        for(int i = 0; i < 4; i++) {
            int nx = x + dx[i], ny = y + dy[i];
            if(nx > 0 && ny > 0 && nx <= n && ny <= m) {
                if(board[nx][ny] != -1) { // 为 -1 表示为万能块元素，可匹配任意颜色
                    set.add(board[nx][ny]);
                }
            } else {
                return -1;
            }
        }
        
        if(set.size() == 1) { // 表示四个格子内的元素都一样（-1与任意匹配）
            Iterator<Integer> iterator = set.iterator();
            return iterator.next(); // 返回该万能块的颜色
        } else {
            return -1;
        }
    }
	
    // 将这块区域设置为 -1，表示万能块
    public static void color(int x, int y) {
        board[x][y] = board[x][y+1] = board[x+1][y] = board[x+1][y+1] = -1;
    }

    public static int nextInt() throws Exception {
        st.nextToken();
        return (int) st.nval;
    }
}

class Node {
    int x, y, k; // (x,y) k:颜色
    public Node(int x, int y, int k) {
        this.x = x;
        this.y = y;
        this.k = k;
    }
}