一、简单释义

1、算法概念

希尔排序是插入排序的一种又称“缩小增量排序”，是直接插入排序算法的一种更高效的改进版本。希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至 1 时，整个文件恰被分成一组，算法便终止。

2、算法目的

把无序数组通过分组，分组之间比较进行移动，最后形成一个有序数组 (文中以升序为例)

3、算法思想

先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2，以此类推。

二、核心思想

先–对已有的数列进行分组，明确增量；
中–每个分组使用直接插入排序进行位置交换；
后–将每个分组执行直接插入排序后的结果在进行直接插入排序；

三、图形展示

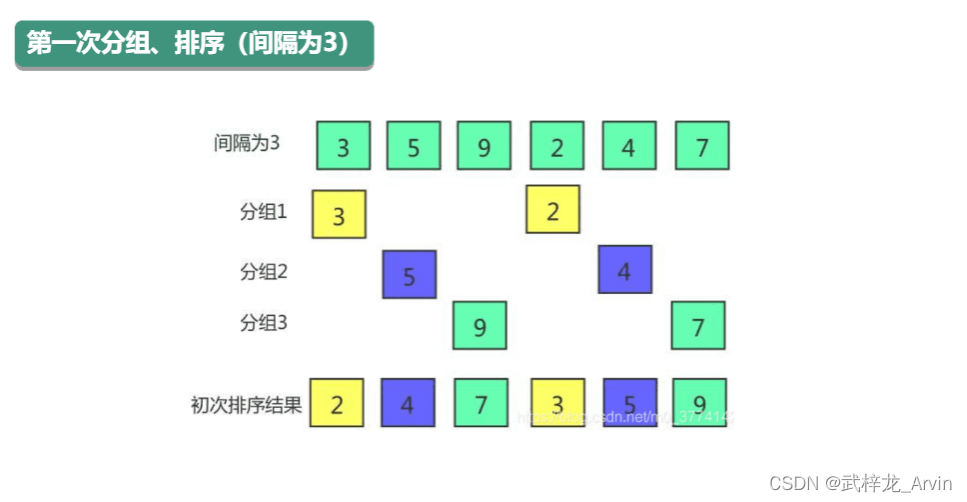
在这里插入图片描述
1、第一次排序：首先明确第一次分组的增量值，用数组的的长度/2。6/2=3，将数组分为增量为3的三个分组，三个分组使用直接插入排序进行位置交换

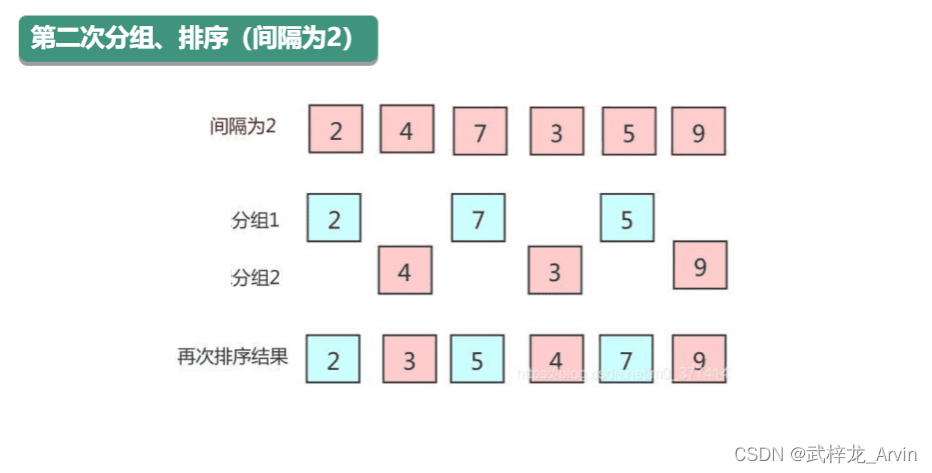
2、第二次排序：首先根据第一次的增量来计算第二次分组的增量，用第一次的增量/2得到第二次的增量，然后进行分组，分组完毕之后使用直接插入排序交换位置。
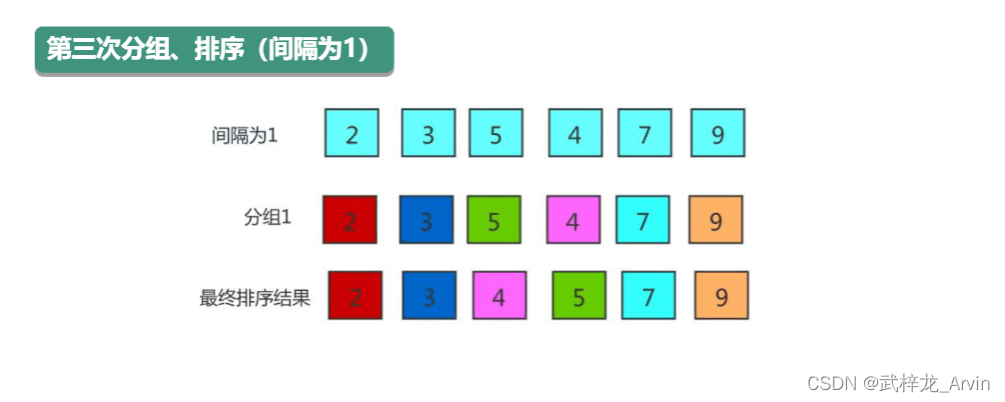
在这里插入图片描述

3、第三次排序：首先根据第二次的增量来计算第三次分组的增量，直到增量为1进行最后一次的排序。

四、代码实现

/**
 * @BelongsProject: demo
 * @BelongsPackage: com.wzl.Algorithm.InsertionSort
 * @Author: Wuzilong
 * @Description: 希尔排序
 * @CreateTime: 2023年5月1日
 * @Version: 1.0
 */

public class ShellSort {

    public static void main(String[] args) {
        int[] arr = {3, 5, 9, 2, 4, 7};
        System.out.println("排序之前数组：");
        System.out.println(Arrays.toString(arr));
        //希尔排序
        insertionSort(arr);

        System.out.println("希尔排序后数组：");
        System.out.println(Arrays.toString(arr));

    }

    private static int[]  insertionSort(int[] arr){
        if(arr == null || arr.length <= 1){
            return arr;
        }
        //希尔排序  升序
        for (int d = arr.length / 2;d>0;d /= 2){ //d：增量  7   3   1
            System.out.println("增量取值:" + d);
            for (int i = d; i < arr.length; i++){
                //i:代表即将插入的元素角标，作为每一组比较数据的最后一个元素角标
                //j:代表与i同一组的数组元素角标
                for (int j = i-d; j>=0; j-=d){ //在此处-d 为了避免下面数组角标越界
                    if (arr[j] > arr[j + d]) {// j+d 代表即将插入的元素所在的角标
                        //符合条件，插入元素（交换位置）
                        swap(arr,j,j+d);
                    }
                }
            }
        }
        return arr;
    }

    public static void swap(int[] arr,int a,int b)
    {
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }
}

运行结果
在这里插入图片描述

五、算法描述

1、问题描述

每一步将一个待排序的元素，按其排序码的大小，插入到前面已经排好序的一组元素的适当位置上去，直到元素全部插入为止

2、算法过程

整个算法过程分为以下几步：
1）通过数组的长度/2得到第一趟排序的增量，按照增量进行分组。
2）每个分组使用直接插入排序进行位置的交换
3）通过第一趟排序的增量/2得到第二次排序的增量，向上取整，在按照增量进行分组。
4）每个分组使用直接插入排序进行位置的交换
5）直到得到的增量为1时，进行的直接插入排序的结果为希尔排序的结果。

3、算法总结

直接插入排序是由两层嵌套循环组成的。外层循环标识并决定待比较的数值。内层循环为待比较数值确定其最终位置。直接插入排序将待比较的数值与它的前一个数值进行比较，所以外层循环是从第二个数值开始的。当前一数值比待比较数值大的情况下继续循环比较，直到找到比待比较数值小的并将待比较数值置入其后一位置，结束该次循环。