本篇博客会讲解整数在内存中的存储形式,以及整数二进制的3种表示形式:原码、反码、补码,还有大小端的相关知识点。相信读完本篇博客,大家对内存的了解会上一个台阶。
注意:本篇博客讨论的是整数在内存中的存储,像char, short, int, long, long long的有符号和无符号类型存储的都是整数。
认识原码、反码、补码
对于整数,有原码、反码、补码之分,它们都是整数的二进制的表示形式。有符号整数的计算方式如下:
- 正整数的原码、反码、补码相同,都是整数直接转换成二进制的结果。
- 负整数的原码是把该数转换成二进制的结果,反码和补码需要通过原码计算出来。
- 负整数的反码的计算规则:原码的符号位不变,其他位按位取反得到反码。
- 负整数的补码的计算规则:反码+1得到补码。
下面来举2个例子,分别表示正整数和负整数。
正整数以10为例子:10作为十进制数,直接转换成二进制,得到的就是它的原码。又因为10是正整数,故原码、反码、补码相同。所以问题呢就转换成如何把十进制的10转换成二进制。
把十进制的10转换成二进制,得到的是1010。这是怎么来的呢?对于二进制的1010,从右往左数,最右边的0代表0×20,倒数第二位的1代表1×21,倒数第三位的0代表0×22,最左边的1代表1×23,所以二进制的1010就代表十进制的1×23+0×22+1×21+0×20=8+0+2+0=10。
严谨点来说:10的默认类型是int,一个int大小是4个字节,也就是32个bit位,应该填满32位,不够在高位补0,所以10的原码、反码、补码都是:00000000000000000000000000001010。
再举个负数的例子:-10的原码、反码、补码是多少?对于负数,是“有符号数”,最高位表示符号位,用1表示负数,其余的位和10的二进制相同:10000000000000000000000000001010。这就是-10的原码。
-10作为一个负数,反码和补码需要通过原码来计算。反码的计算规则是,原码符号位不变,其他位按位取反,也就是说,最高位的1表示符号位,不变,其余位1变0,0变1。反码就是:11111111111111111111111111110101。
补码的计算规则是:反码+1即是补码,所以-10的补码是:11111111111111111111111111110110。
整数在内存中是以哪种形式存储的呢?事实上,整数在内存中存储的是二进制的补码,这一点是可以验证的,但是同时涉及到大小端的问题。
大小端字节序
大小端字节序,简称大小端,指的是,以字节为单位,内存中的数据是如何存储的。分为2种存储方式,分别是大端字节序和小端字节序,简称大端和小端。
- 大端字节序:把高位字节处的数据存储在低地址处,把低位字节处的数据存储在高地址处。
- 小端字节序:把高位字节处的数据存储在高地址处,把低位字节处的数据存储在低地址处。
这是什么意思呢?我在VS2022环境下验证一下:根据前面所讲,整数在内存中存储的是补码,我们来观察一下-10在内存中是如何存储的。
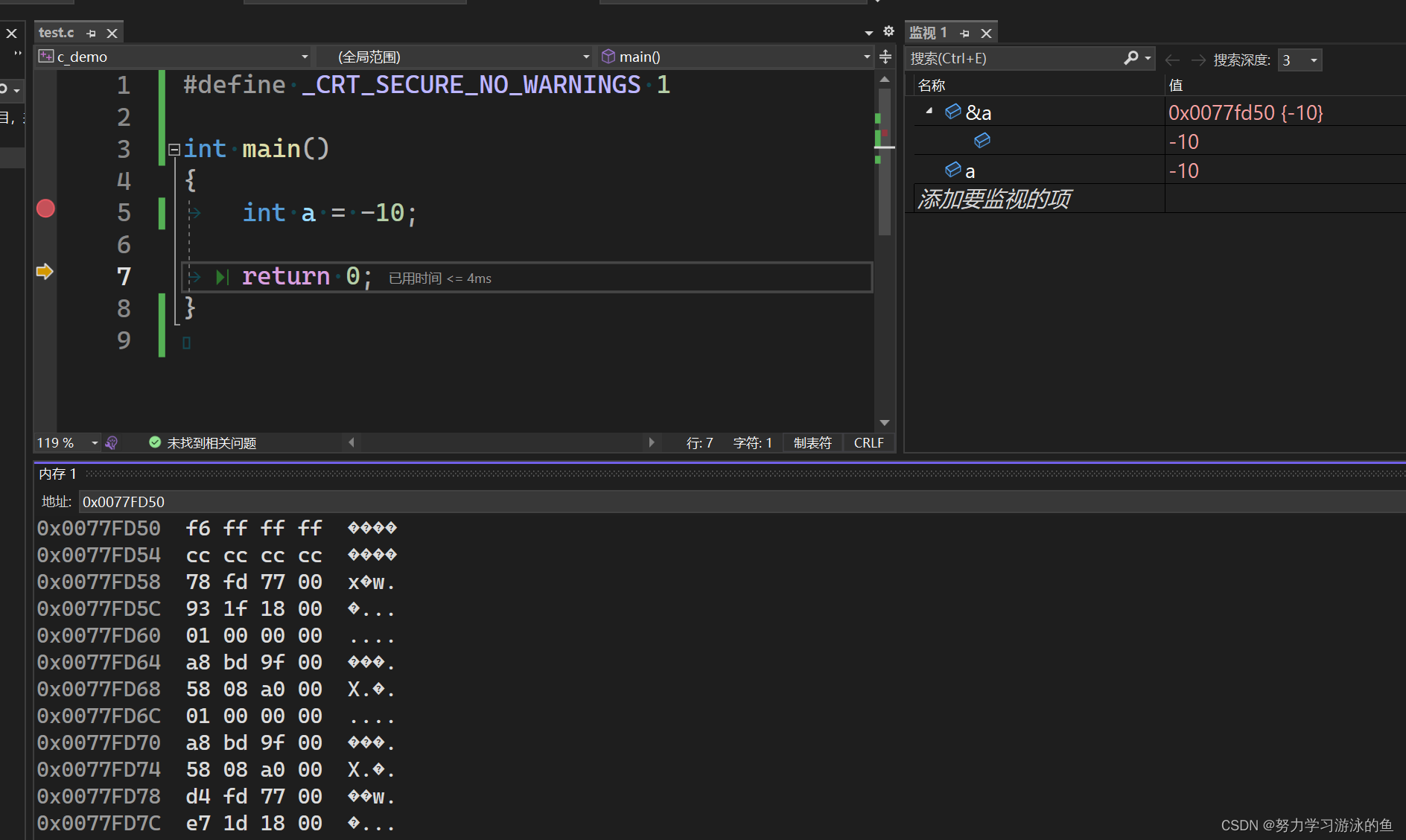
观察到,当左边是低地址,右边是高地址,即地址从左到右是由低到高变化的,此时内存中存储的是0x f6 ff ff ff。这是什么意思呢?
整数在内存中是以二进制的补码的形式存储的。前面计算过了,-10的补码是:11111111111111111111111111110110。下面我们把它转换成十六进制。
先4个为一组分开:1111 1111 1111 1111 1111 1111 1111 0110。
然后分别转换每一组,其中1111是f,0110是6:0x fffffff6。一个十六进制位是4个bit位,2个十六进制位就是一个字节,把这个数以字节为单位分隔开,就是:0x ff ff ff f6。
而内存中存储的却是:0x f6 ff ff ff,这是为什么呢?在VS环境下观察内存,从左到右,地址是由低到高变化的,也就是说,本来-10补码中的高位的ff存储在了高地址处,而-10补码中的低位的f6存放在低地址处,这就是“小端字节序”的存储方式,看起来像是数据“倒着放”。
整数在内存中的存储
整数在内存中的存储,是由以下2点决定的:
- 整数在内存中存储的是补码的二进制。
- 根据机器是“大端字节序”还是“小端字节序”来决定是“正着放”还是“倒着放”。
以上是数据“如何存”,那如何把一个数据“往外拿”呢?把存的过程倒过来就行了。
- 根据大小端字节序,把数据“正着”或者“倒着”拿出来。
- 把拿出来的补码转换成原码。
那如何把补码转换成原码呢?原码怎么转换成补码,把这个过程倒过来就行了,以下是如何把补码解析成有符号数的过程。
- 若符号位是0,则是正数,此时原码、反码都和补码相同。若符号位是1,则是负数,需要计算反码和原码。
- 补码-1得到反码。
- 反码的符号位不变,其他位按位取反得到原码。
注意:如果要解析成无符号数,最高位就不是符号位了,而是数据的一部分,此时一律看做正整数来处理。
举个例子,前面我们观察到小端机器下-10在内存中存储的是:0x f6 ff ff ff,由于小端是“倒着存”的,所以先正过来:0x ff ff ff f6,再转换成二进制:1111 1111 1111 1111 1111 1111 1111 0110,即11111111111111111111111111110110,这就是补码,由于符号位(最高位)是1,是一个负数,需要根据补码计算反码和原码。先把补码-1,得到反码:11111111111111111111111111110101,把反码符号位不变,其他位按位取反得到原码:10000000000000000000000000001010,再转换成十进制,就得到了-10。
为什么要存补码?
整数在内存中存储的是补码的二进制,这主要有2个优点。
先说第一个优点:使用补码来存储,统一了符号位和数值位。换句话说,符号位和数值为可以统一计算。在CPU中,只有加法器,所有的计算都要转换成加法。比如,计算1-1,先要转换成计算1+(-1),然后写出1和-1的补码:
1作为正数,原码、反码、补码相同,都是:00000000000000000000000000000001
-1作为负数,原码是:10000000000000000000000000000001,原码符号位不变,其他位按位取反后得到反码:11111111111111111111111111111110,反码+1得到补码:11111111111111111111111111111111。
接下来计算1+(-1),也就是这样计算:
00000000000000000000000000000001
+ 11111111111111111111111111111111
100000000000000000000000000000000
由于整数只能存储32个bit为,最高位的1就丢了,只剩下00000000000000000000000000000000,得到的结果就是0。
根据以上的计算,有没有发现,我们根本没有管哪里是符号位,哪里是数值位,就是简单粗暴的把补码写出来,加起来,完事。CPU把内存中存储的补码拿出来,进行加法运算时,根本不用考虑哪里是符号位,那里是数值位,这就做到了把符号位和数值位统一处理。
在说第二个优点之前,还需要了解一个知识点:把补码转换成原码的另一种方式:先把补码的符号位不变,其他位按位取反,再+1,也能得到原码。比如:已知-10的补码:11111111111111111111111111110110,把补码的符号位不变,其他位按位取反得到:10000000000000000000000000001001,再+1得到:10000000000000000000000000001010,这样也得到了-10的原码。
有没有发现,如果用这种方式把补码转原码,那么就和原码转补码的方式相同了,都是“取反再+1”!所以,用补码来存储时,把补码转原码,以及原码转补码可以使用同一套硬件电路,降低了电路的复杂性。
总结
- 整数的2进制有3种表示形式,分别是原码、反码、补码。
- 正整数的原码、反码、补码相同,负整数的原码、反码、补码需要计算。把整数直接转换成2进制,就是原码。负整数的原码的符号位不变、其他位按位取反得到反码。负整数的反码+1得到补码。
- 从补码转原码,需要先看符号位,确定是正数还是负数,如果是正数,则原码、反码、补码相同。如果是负数,则可以先-1得到反码,再符号位不变,其他位按位取反得到原码;也可以先符号位不变,其他位按位取反,再+1得到原码。注意:无符号数一律按照正数来处理。
- 大小端字节序分为大端字节序和小端字节序。大端字节序指的是,把高位字节处的数据存储在低地址处,把低位字节处的数据存储在高地址处。小端字节序指的是,把高位字节处的数据存储在高地址处,把低位字节处的数据存储在低地址处。
- 内存中使用补码来存储整数有2个好处:统一处理符号位和数值位,以及使用同一套硬件电路来把原码和反码相互转换,降低电路复杂性。
感谢大家的阅读!