文章目录
- 基本概念
- 图有两种基本形式
- 无向图的表示
- 有向图的表示
基本概念
- 图结构也是数据结构的一部分。而且还有一点小难。
- 图是由多个结点链接而成的,但是一个结点可以同时连接多个其他结点,多个节点也可以同时指向一个节点。【多对多的关系】
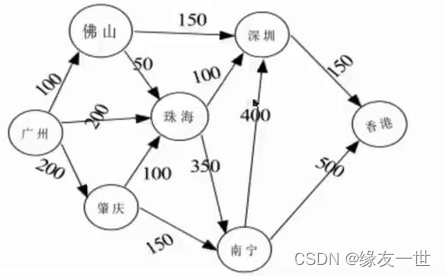
- 图结构是任意两个数据对象之间都有可能存在某种特点关系的数据结构。

- 图(Graph)一般由两个集合共同构成
- 一个是非空但是有限的顶点集合V(Vertex)
- 另一个是描述顶点之间连接关系的边集合日(Edge,边集合可以为空集【一个节点的情况】)
- ***一个图实际上正是由结点(顶点)和对应的边组成的。***因此,图的表示为: G = ( V , E ) G=(V,E) G=(V,E)
- 结点的度:就是与其连接的边数
图有两种基本形式
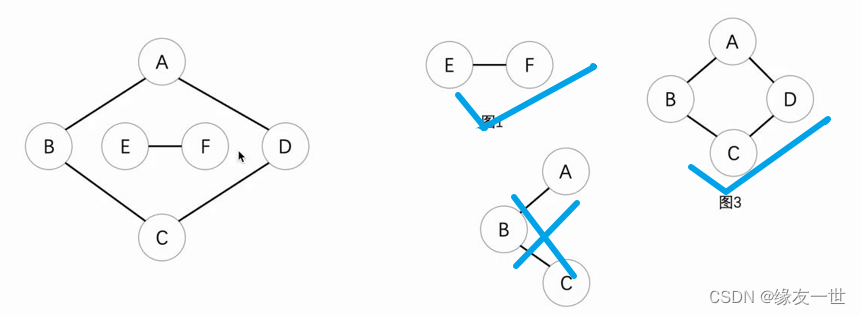
无向图的表示
- 无向图仅仅是连接,并不指明方向
- 集合
V
=
A
,
B
,
C
,
D
,
E
V={A,B,C,D,E}
V=A,B,C,D,E集合KaTeX parse error: Expected '}', got 'EOF' at end of input: …,D),(D,A),(C,A)
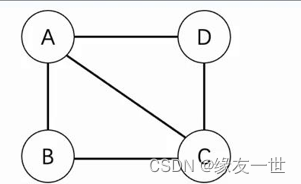
有向图的表示
- 有向图标记明了方向
- 集合
V
=
A
,
B
,
C
,
D
,
E
V={A,B,C,D,E}
V=A,B,C,D,E集合
E
=
<
A
,
B
>
,
<
B
,
C
>
,
<
C
,
D
>
,
<
D
,
A
>
,
<
C
,
A
>
E={<A,B>,<B,C>,<C,D>,<D,A>,<C,A>}
E=<A,B>,<B,C>,<C,D>,<D,A>,<C,A>
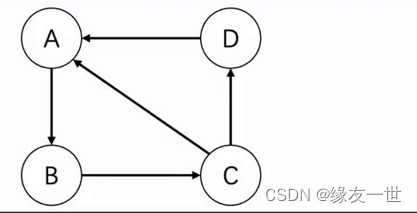
- 邻接点:无向图存在一条边(A,B),就称A,B互为邻接点。如果是有向图的一条边<A,B>,就称起点A邻接到终点B。
- 出度:与顶点相连且指向该顶点的边的个数。
- 入度:与顶点相连且指向邻接顶点的边的个数。
- 简单图:图中不存在回路或重边。
- 非简单图:图中存在贿回路或者重边。

- 无向完全图:在一个无向图中,任意两个顶点都有一条边相连。
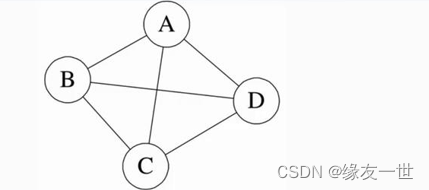
- 有向完全图:在有向图中,任意两顶点之间都有由方向互为相反的两条边连接。
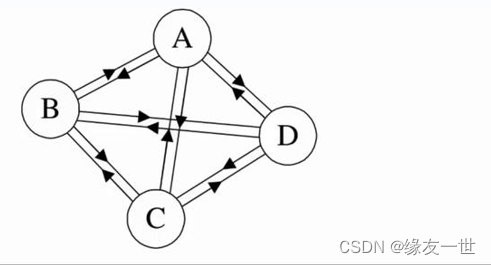
- 顶点连通:在一个无向图中,存在一个顶点到另一个顶点的路径。
- 连通图:一个无向图中任意两点都是连通的。
- 强连通图:一个有向图中任意顶点A和B,存在两者之间相互的带方向路径。
- 子图:对于图
G
=
(
V
,
E
)
G=(V,E)
G=(V,E)和
G
′
=
(
V
′
,
E
′
)
G'=(V',E')
G′=(V′,E′),若满足
V
′
V'
V′是
V
′
V'
V′的子集。
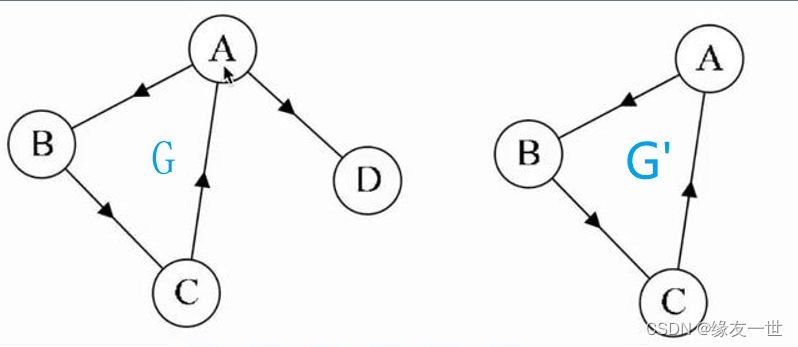
- 极大连通子图:连通子图是原图的子图,并且子图也是连通图,同时具有最大的顶点数。即在加入原图中,其他顶点会导致子图不连通。拥有极大顶点数的同时也要包含。依附于这点顶点所有的边。
- 连通分量:无向图的极大连通子图
- 强连通分量:有向图的极大连通子图。