目录
一.连续子数组最大和
方法2动态规划
二.查找最小的k对数字
一.从先序遍历还原二叉树
二.完全二叉树
三.判断对称二叉树
四 回文
五.连续子数组最大和
六.TopK问题
思路一如果数据特别大.排序的时间复杂度会很大
思路二:用大根堆或者小根堆然后分别弹出.
思路三:前k堆
七.堆元素排序
八.对象的比较
1.equals:用来比较两个对象相不相同
2.使用compaerable接口
3.Comparator比较器比较
4.总结
5.将优先级队列变成大根堆
一.连续子数组最大和
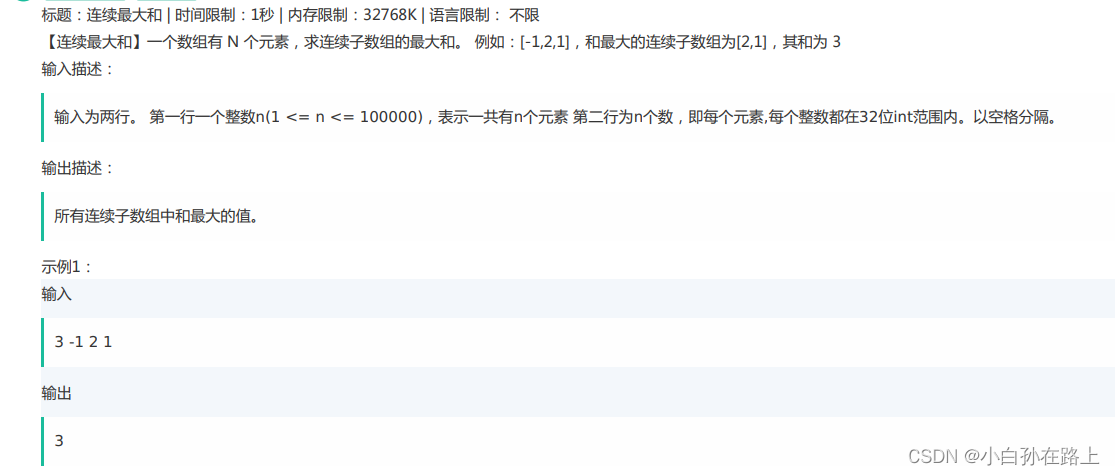
1.暴力解法
i从第一个元素开始.j从第二个元素开始,然后j开始遍历,计算每个大小.如果第二次比上次大就换成这次的
i再从第二个元素开始,j再从第三个元素开始遍历一直反复计算算到最大值,这里的时间复杂度就是O(n2);
public int FindGreatestSumOfSubArray (int[] array) {
// write code here
int len=array.length;
int max=array[0];
for (int i = 0; i < len; i++) {//只要到最后一个,j也进不去循环,就不会数组越界
int sum=array[i];
if(sum>max){
max=sum;
}
for (int j = i+1; j <len ; j++) {
sum+=array[j];
if(sum>max){
max=sum;
}
}
}
return max;
}
}这里注意,如果都是负数,很有可能直接输出0所以最好让max初始为数组第一个元素,但是这种算法复杂度过大
方法2动态规划
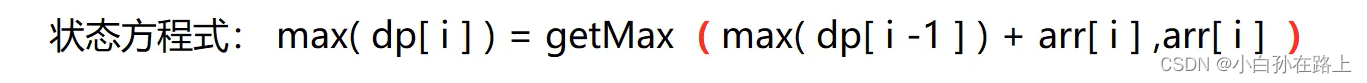
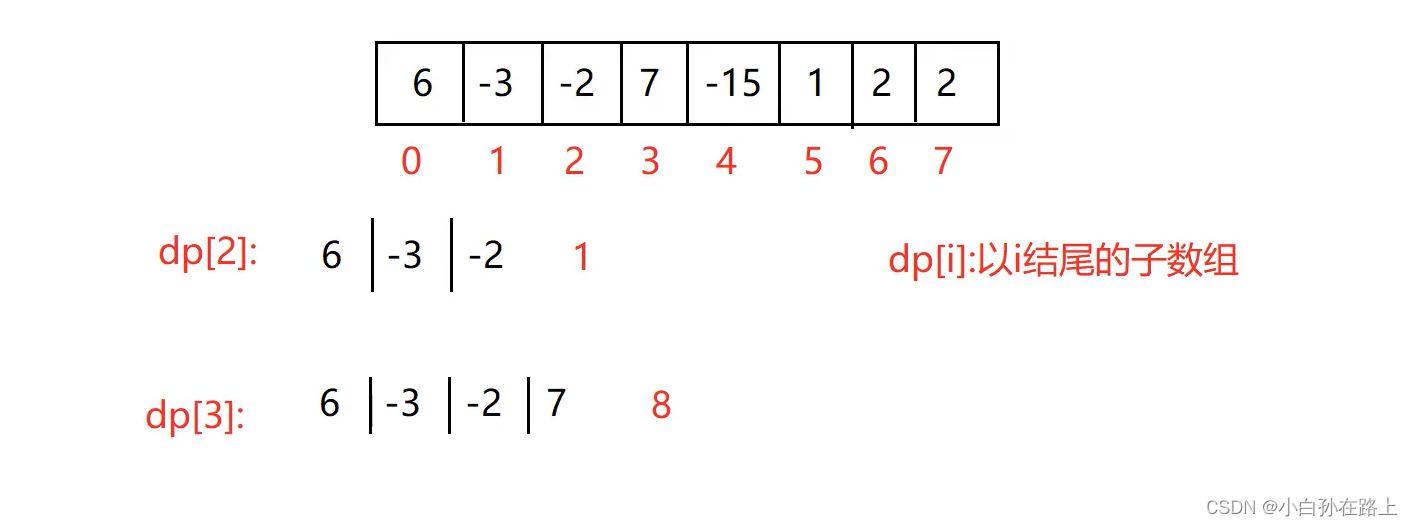
定义一个max和sum初始值都为第一个元素,然后往后遍历,因为子数组最大要么是前面的加上本身,要么就是本身,
public int getMax(int a,int b){
return a>b?a:b;
}
public int FindGreatestSumOfSubArray (int[] array) {
int sum= array[0];
int max=array[0];
for (int i = 1; i < array.length; i++) {
sum=getMax(sum+array[i],array[i]);
max=sum>max?sum:max;
}
return max;
}
}
二.查找最小的k对数字
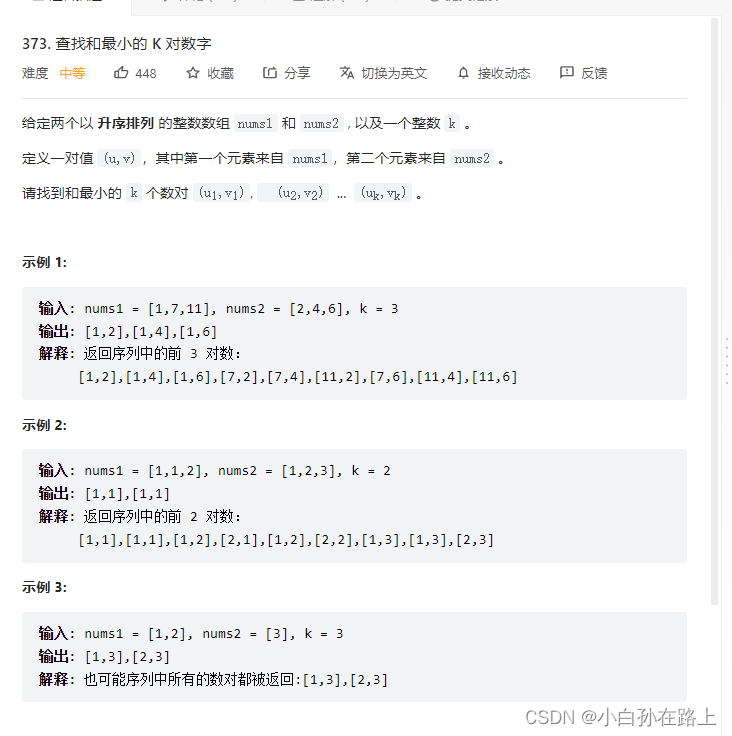
首先这道题我们用的是优先队列的方法
因为优先队列底层是一个小根堆,我们需要重写一个比较建立一个内部类
改变比较的方式
然后开始循环,
因为会有k的大小大于遍历的情况
所以需要范围需要在k和数组长度找个最小值,因为
i没必要都走完,就看k的大小就行.因为这是一个升序的数组.
然后建立k个大小的大堆
建立一个顺序表把元素放进里面
再放进优先队列里
放完之后再判断剩下的有没有比他第一个元素大
也就是堆顶元素.因为他是大根堆,堆顶元素一定是最大的
如果比大根堆还大.那就直接换下,找最小的,
但是如果不大.就可以直接跳出循环.因为这是一个升序数组,现在不大以后都会不大
就不用再往后遍历了
因为题目要的是
![]()
所以建立一个顺序表
接收优先队列弹出的元素
但是有可能k的值过大,还没弹到第k个,优先表就空了,所以这个时候就需要再建立一个条件,就是他不为空

class Solution {
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k){
PriorityQueue<List<Integer>> priority=new PriorityQueue<>(new Comparator<List<Integer>>() {
@Override
public int compare(List<Integer> o1, List<Integer> o2) {
return o2.get(0)+o2.get(1)-o1.get(0)-o1.get(1);
}//大根堆
});
for (int i = 0; i <Math.min(k,nums1.length); i++) {
// List<Integer> list=new ArrayList<>();
for (int j = 0;j<Math.min(k,nums2.length); j++) {
if(priority.size()<k){
List<Integer> tmpList=new ArrayList<>();
tmpList.add(nums1[i]);
tmpList.add(nums2[j]);
priority.offer(tmpList);
}else{
if(nums1[i]+nums2[j]<priority.peek().get(0)+priority.peek().get(1)){
List<Integer> tmpList=new ArrayList<>();
tmpList.add(nums1[i]);
tmpList.add(nums2[j]);
priority.poll();
priority.offer(tmpList);
}else{
break;
}
}
}
// priority.offer(list);
}
List<List<Integer>> lists=new ArrayList<>();
while(!priority.isEmpty()) {
lists.add(priority.poll());
}
return lists;
}
}一.从先序遍历还原二叉树
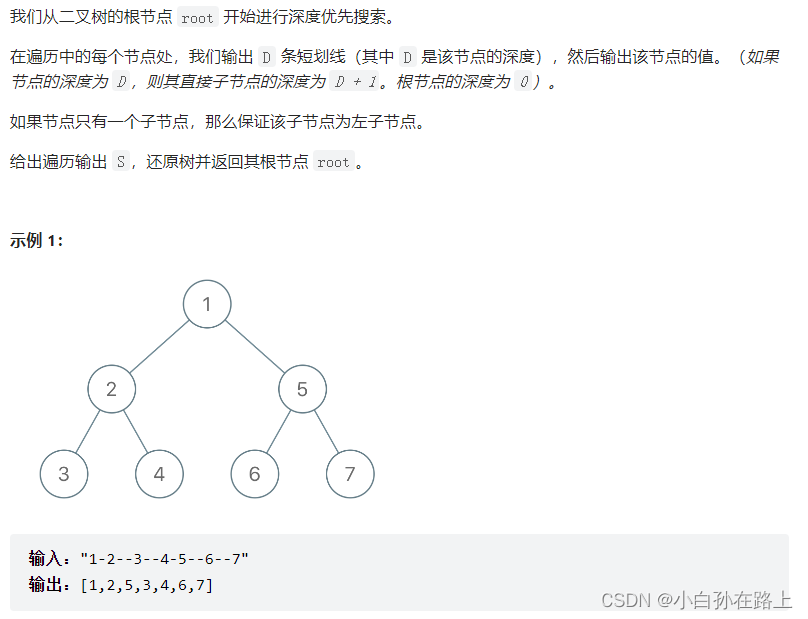
这道题我们考虑模拟递归的方式
之前层序遍历我们用的是队列:因为先进先出
而这里我们一般用的是栈来模拟递归
我们定义一个变量记录每个节点的高度
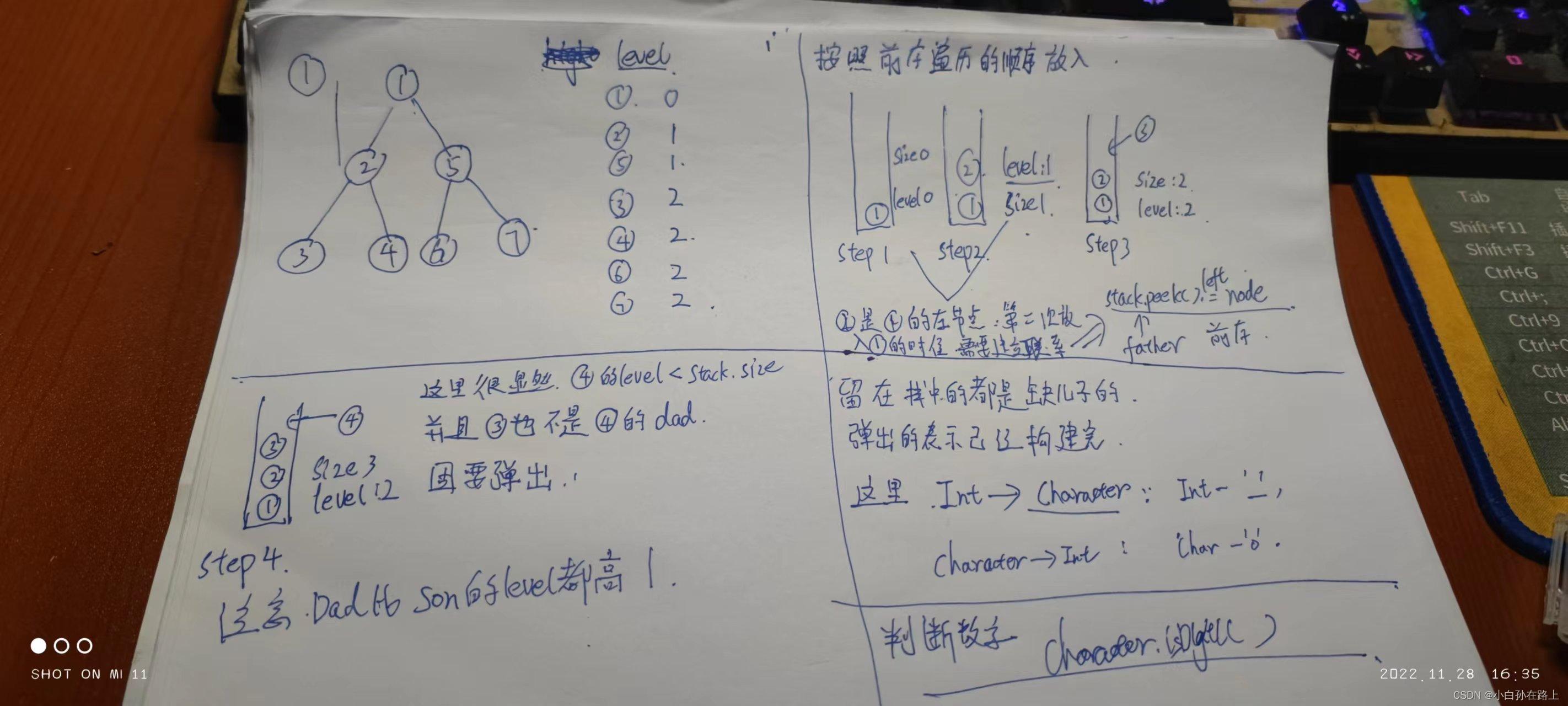


class Solution {
public TreeNode recoverFromPreorder(String traversal) {
char[] arr=traversal.toCharArray();
Stack<TreeNode> stack=new Stack<>();
int i=0;
while(i<arr.length){
int level=0;
int val=0;
while(i<arr.length&&arr[i]=='-'){
i++;
level++;
}//计算多少- 并跳过
while(i<arr.length&&Character.isDigit(arr[i])){ //防止最后一个跳出循环,数组越界
val=val*10+(arr[i]-'0');//变成数字
i++;
}//到了这里数组下标指向了下一个-了
TreeNode node=new TreeNode(val);//建立新的节点
if(0==stack.size()){
stack.push(node);//第一个的情况
}else{//要么大于要么等于
while(stack.size()!=level){
stack.pop();
}//到了这里就一定相同
TreeNode fatherNode=stack.peek();
if(fatherNode.left==null){
fatherNode.left=node;
}else{
fatherNode.right=node;
}
stack.push(node);//不要忘记放进去
}
}
while(stack.size()>1){
stack.pop();
}
return stack.peek();
}
}二.完全二叉树
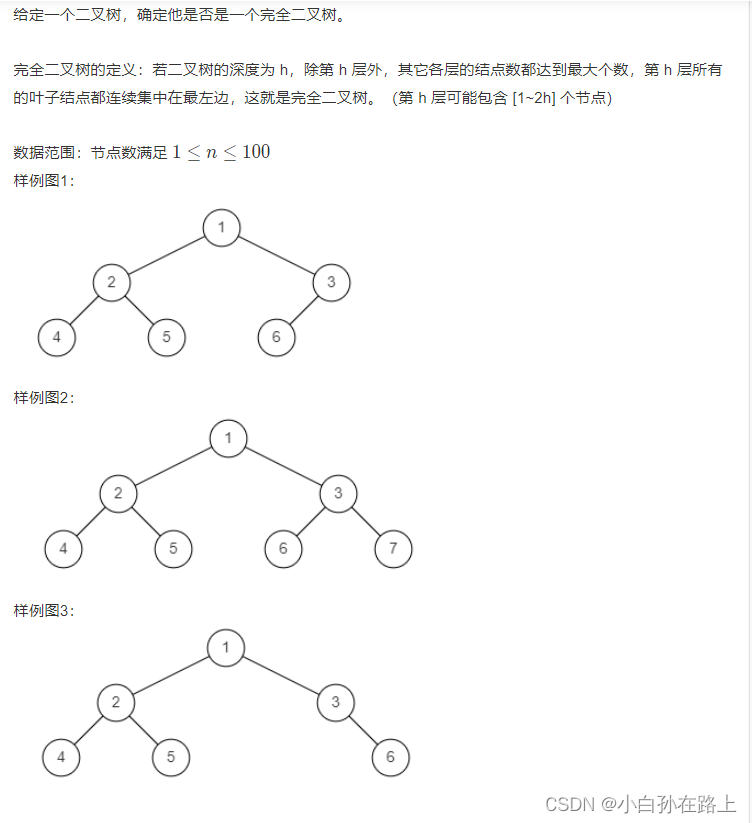
思路:用层序遍历的思路分别放入节点
每放一层就判断是否为null然后弹出
并放入他的左右节点(按顺序)
再循环
每层每层的放弹出,用队列,因为队列可以保证先进先出
先放左节点可以让左节点先判断
原理就是如果不是完全二叉树,如果左右节点顺序放.有null.就会保证在检查出null的时候,后面还有节点
但是如果是完全二叉树是不可能出现这种情况
public boolean isCompleteTree (TreeNode root) {
Queue<TreeNode> queue=new LinkedList<>();
if(root==null) return true;
queue.offer(root);
while(!queue.isEmpty()){
TreeNode top= queue.remove();
if(top==null){
break;
}
queue.offer(top.left);
queue.offer(top.right);
}
while(!queue.isEmpty()){
TreeNode top= queue.remove();
if(top!=null){
return false;
}
}
return true;
}
}三.判断对称二叉树
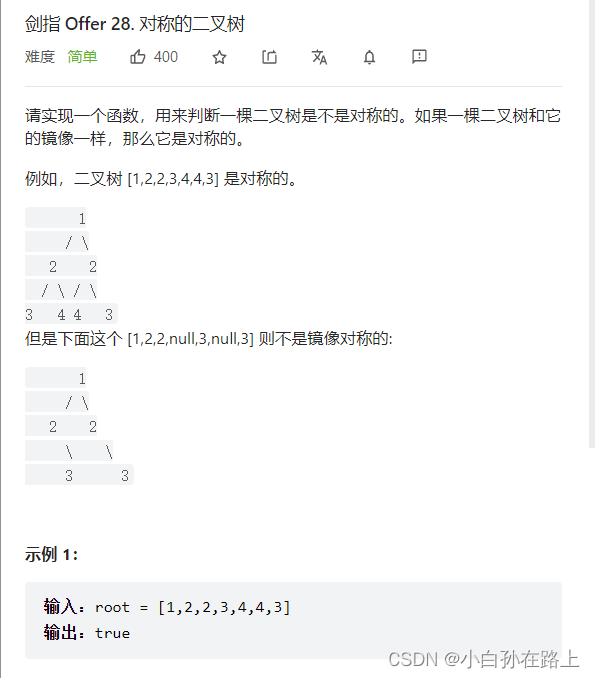
首先要结构相同,如果是一个是null一个不是就不可以
而且除了根其他的要全部对称.也就是左节点和右节点相同
所以需要写两个方法
class Solution {
public boolean isSame(TreeNode p,TreeNode q){
if(p==null&&q!=null) return false;
if(p!=null&&q==null) return false;
if(p==null&&q==null) return true;
if(p.val!=q.val) return false;
return isSame(p.left,q.right)&&isSame(p.right,q.left);
}
public boolean isSymmetric(TreeNode root) {
if(root==null) return true;
return isSame(root.left,root.right);
}
}因为原本的方法参数只有一个,但是判断需要同时判断左边和右边,所以需要再写一个方法
四 回文


这个题目要对字符串方法非常的熟悉
首先不能对字符串本身插入,非常就改变了原来的字符串
所以我们需要新建一个对象来改变
因为插入函数只有sb有
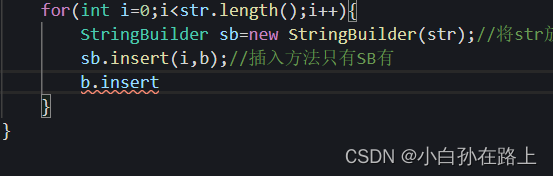
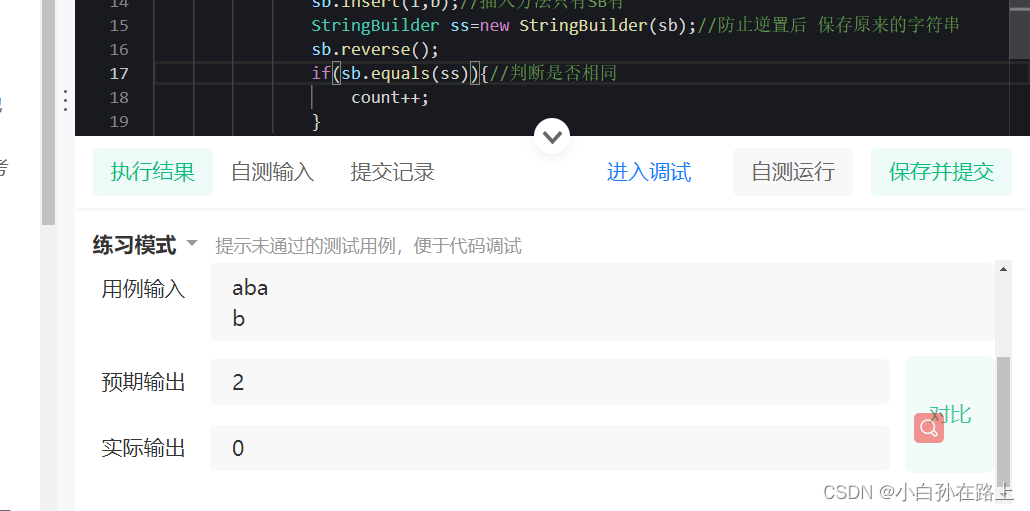
这里注意,StringBuilder没有equlal方法需要转成字符串
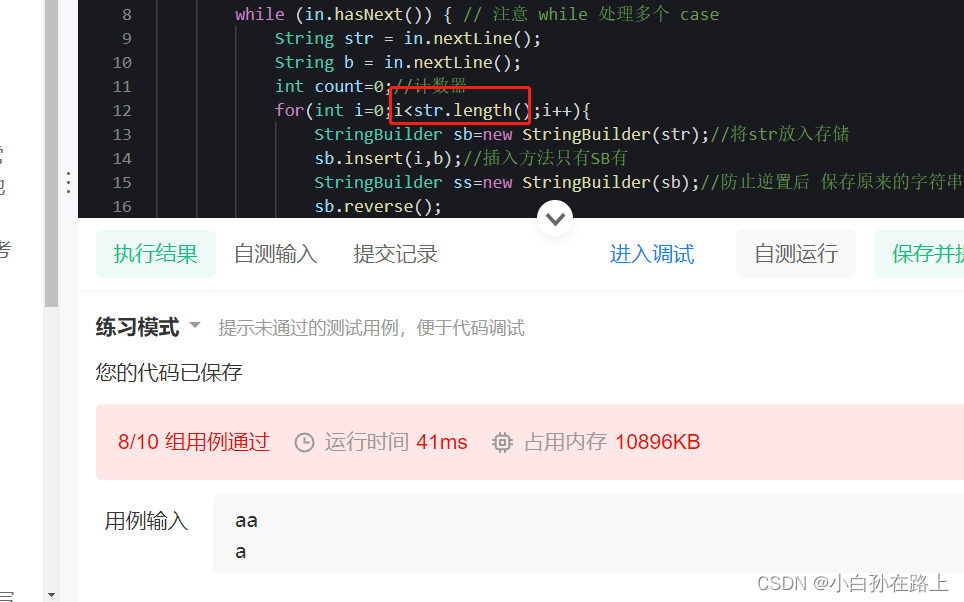
这里注意,a假设有2 但是插入会多多插一个位置,所以就会少判断
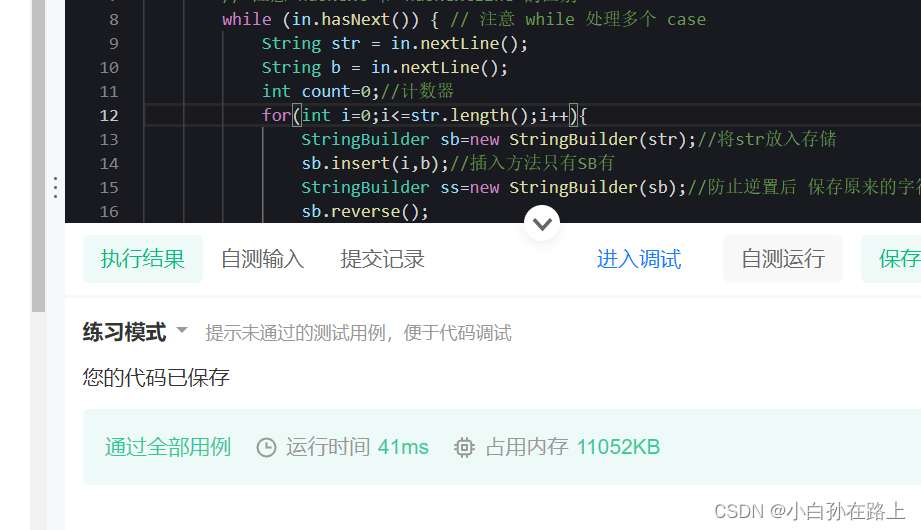
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
while (in.hasNext()) { // 注意 while 处理多个 case
String str = in.nextLine();
String b = in.nextLine();
int count=0;//计数器
for(int i=0;i<=str.length();i++){
StringBuilder sb=new StringBuilder(str);//将str放入存储
sb.insert(i,b);//插入方法只有SB有
StringBuilder ss=new StringBuilder(sb);//防止逆置后 保存原来的字符串
sb.reverse();
if(sb.toString().equals(ss.toString())){//判断是否相同
count++;
}
}
System.out.println(count);
}
}
}
写一个判断回文的方法
public static boolean reverse(StringBuilder sb){
int left=0;
int right=sb.length()-1;
char[] ch=sb.toString().toCharArray();
while(left<right){
if(ch[left]!=ch[right]){
return false;
}
left++;right--;
}
return true;
}五.连续子数组最大和
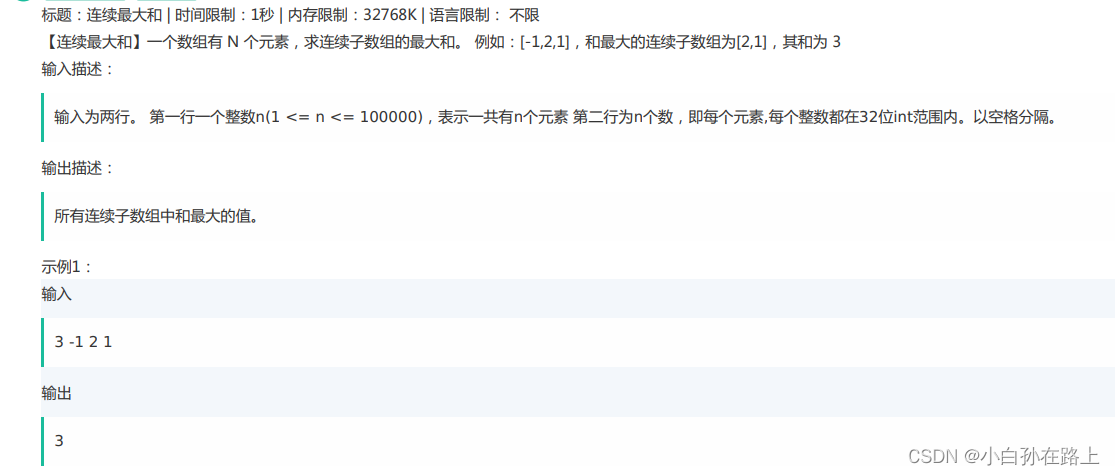
六.TopK问题
思路一如果数据特别大.排序的时间复杂度会很大

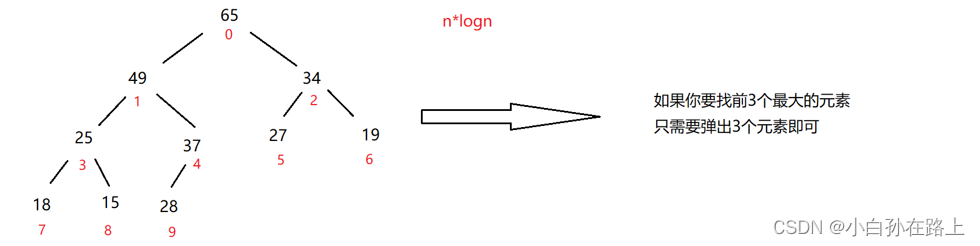
思路二:用大根堆或者小根堆然后分别弹出.
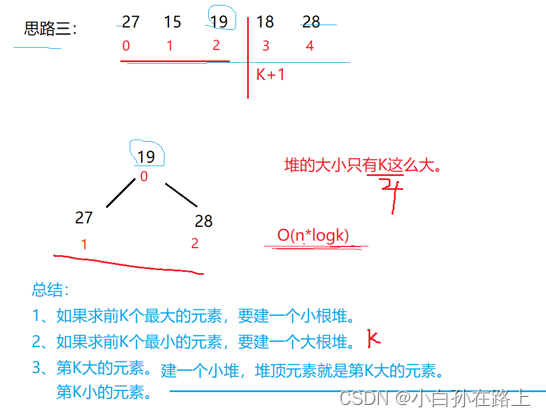
思路三:前k堆
求前k个最大元素.就把前k个元素建立成一个小根堆.如果有比堆顶大的.就换成他

因为只能根堆顶元素比.剩下两个元素可能比要比的元素小,但是都替换不了.
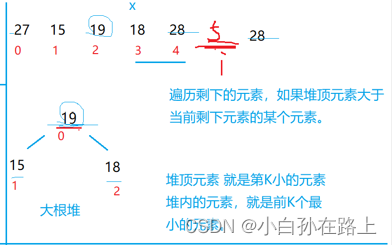
代码的实现
/**
* 求数组当中前k个最小的元素
* @param //args
*/
public static int[] topK(int[] arr,int k){
PriorityQueue<Integer> maxHeap=new PriorityQueue<>(k, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;//创建一个大小为k的大根堆
}
});
for (int i = 0; i < arr.length; i++) {
if(maxHeap.size()<k){
maxHeap.offer(arr[i]);//依次放前k个元素
}else{
//从第k+1开始根堆顶元素比较,如果小,就换上去
if(arr[i]<maxHeap.peek()){
//先弹出
maxHeap.poll();
//再放入
maxHeap.offer(arr[i]);
}
}
}
int[] tmp=new int[k];
for (int i = 0; i < k; i++) {
tmp[i]=maxHeap.poll();
}
return tmp;
}
public static void main(String[] args) {
int[] arr={18,21,8,10,34,12};
int[] tmp=topK(arr,3);
System.out.println(Arrays.toString(tmp));
}为什么是大根堆因为一定要保证每次都跟最大的比较,然后把最大的换掉,所以最后剩下的一定是最小的
tmp是引用变量直接打印打印不出来,要用tostring方法
这道题用优先级队列做,因为优先级队列底层是小根堆,因为要找前k最小的,所以需要大根堆,比较
class Solution {
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k){
PriorityQueue<List<Integer>> priority=new PriorityQueue<>(new Comparator<List<Integer>>() {
@Override
public int compare(List<Integer> o1, List<Integer> o2) {
return o2.get(0)+o2.get(1)-o1.get(0)-o1.get(1);
}//大根堆
});
for (int i = 0; i <Math.min(k,nums1.length); i++) {//防止k比length大,还要继续弹会造成数组越界
// List<Integer> list=new ArrayList<>();
for (int j = 0; j < Math.min(k,nums2.length); j++) {
if(priority.size()<k){
List<Integer> tmpList=new ArrayList<>();
tmpList.add(nums1[i]);
tmpList.add(nums2[j]);
priority.offer(tmpList);
}else{
List<Integer> tmpList=new ArrayList<>();
tmpList.add(nums1[i]);
tmpList.add(nums2[j]);
if(tmpList.get(0)+tmpList.get(1)<priority.peek().get(0)+priority.peek().get(1)){
priority.poll();
priority.offer(tmpList);
}
}
}
// priority.offer(list);
}
List<List<Integer>> lists=new ArrayList<>();
for (int i = 0; i < k&&!priority.isEmpty(); i++) {
lists.add(priority.poll());
}
return lists;
}
}七.堆元素排序


因为要求数据从0下标到9下标从小到大.应该借助大根堆
找到最大元素再0号下标.然后再放到最后一个元素
再让总元素--(因为最后一个排序好了.不用再排序了)

代码的实现
public void heapSort(){
int end=usedSize-1;//这样就非常巧妙
while(end>0){
int tmp=arr[0];
arr[0]=arr[end];
arr[end]=tmp;//
shiftDown(0,end);//这里传过去的时候end就已经去掉了最后一个
end--;
}
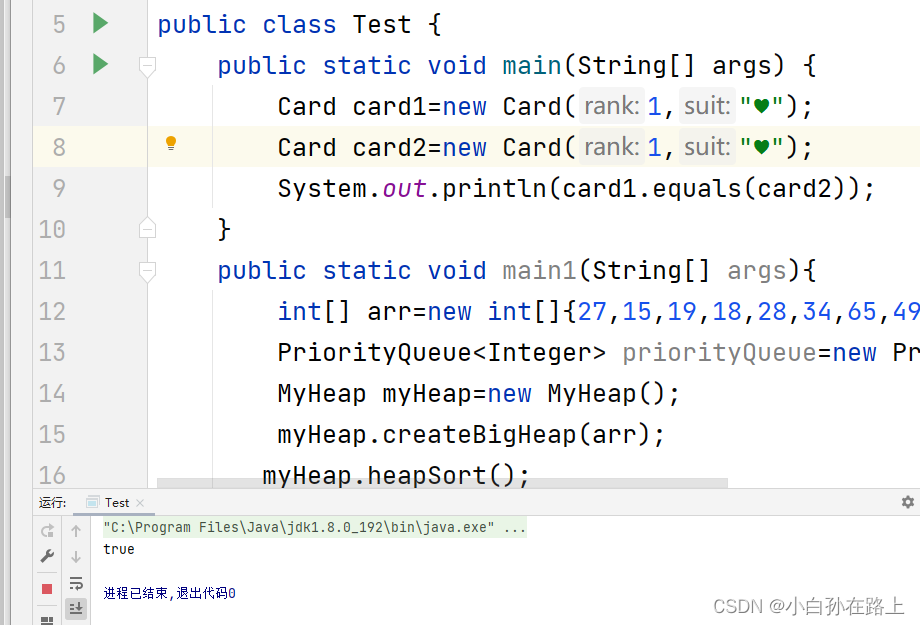
}八.对象的比较
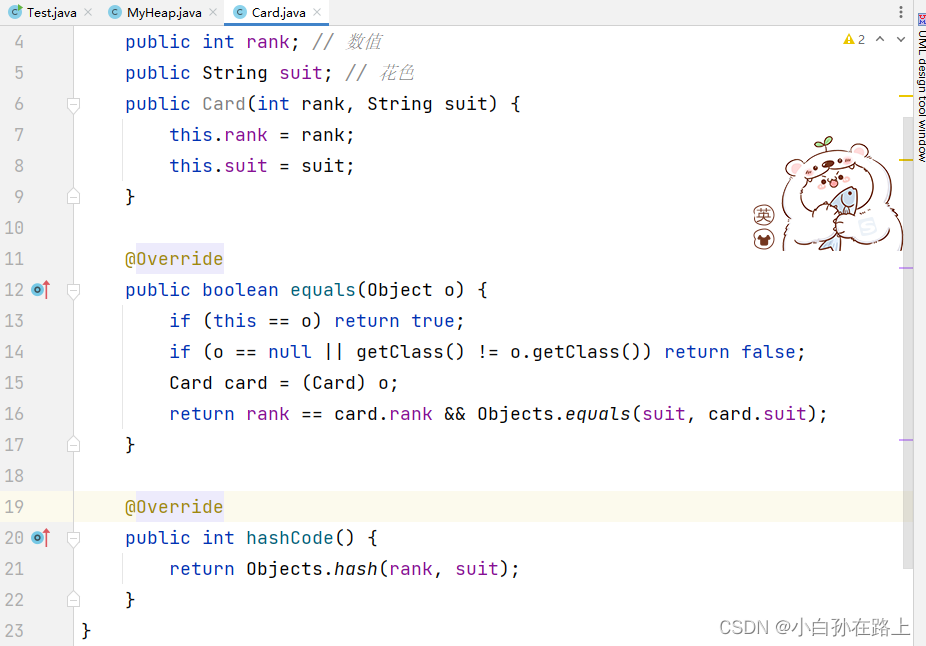
1.equals:用来比较两个对象相不相同
如果是基本类型可以用equals
但是如果是自定义类,需要重写.
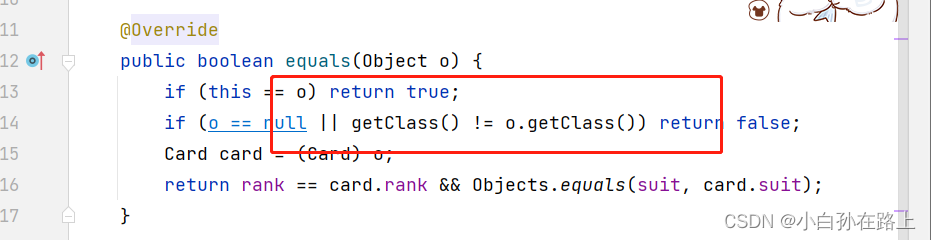
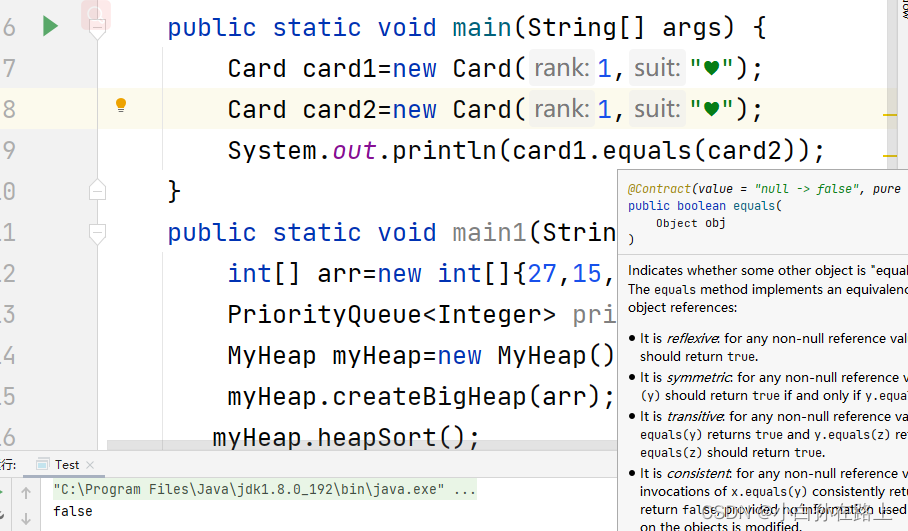
看是否是同一个类,或者另外一个是否是空的
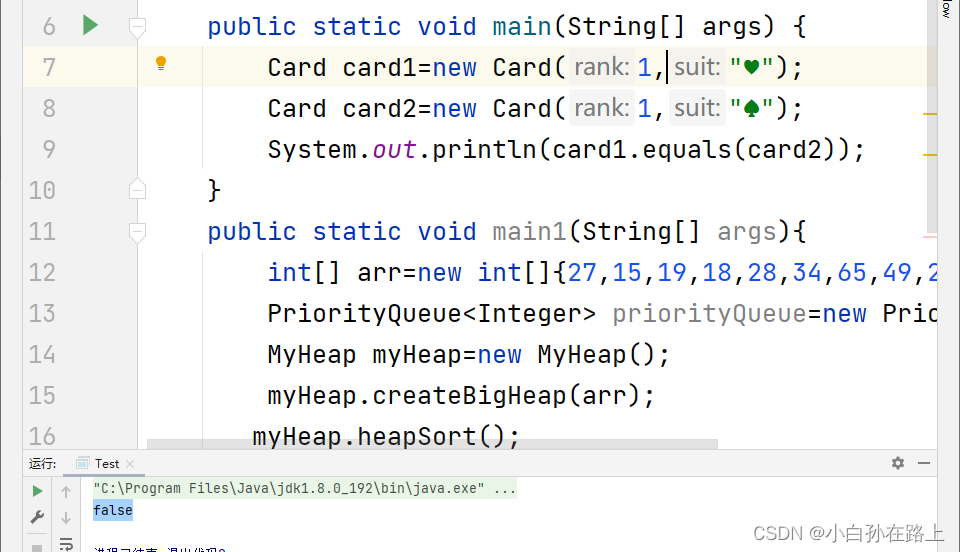
必须成员全部相同
如果没有重写就默认用父类的
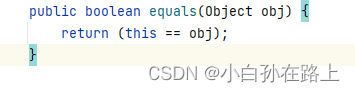
引用类型比较 要看地址比较,不是同一个对象地址不一样
2.使用compaerable接口
在类中使用Compareable接口并重写Compaeto方法
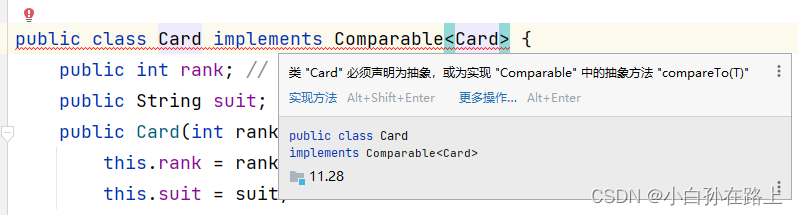
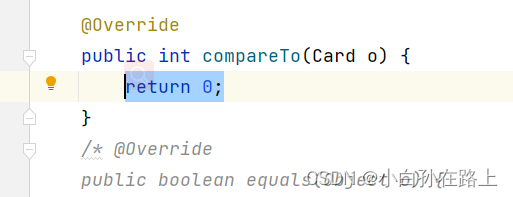
这块得自己写,如果我们想要从大王小排序就需要
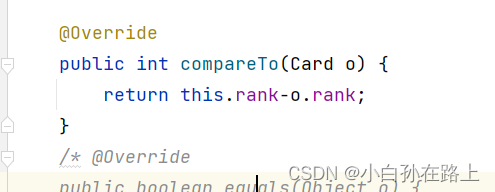

这里发现.priorityQueue就自动排序了

第一次p添加一张牌
刚开始size=0
因为priorityQueue底层默认是个数组
数组长度默认是11
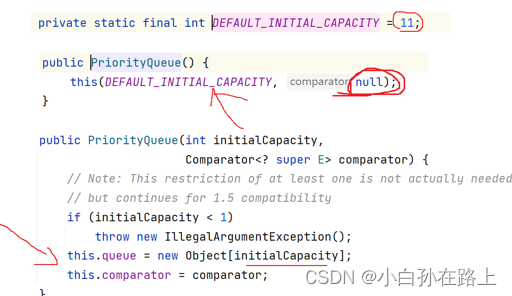
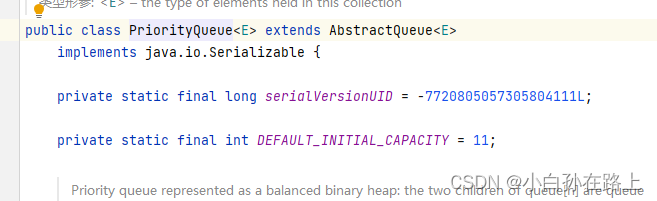

如果长度不够就要扩容
如果i是0 就放在第一个下标

如果放第二个元素
就要向上调整

可以发现,调用构造方法的时候,comparator是null
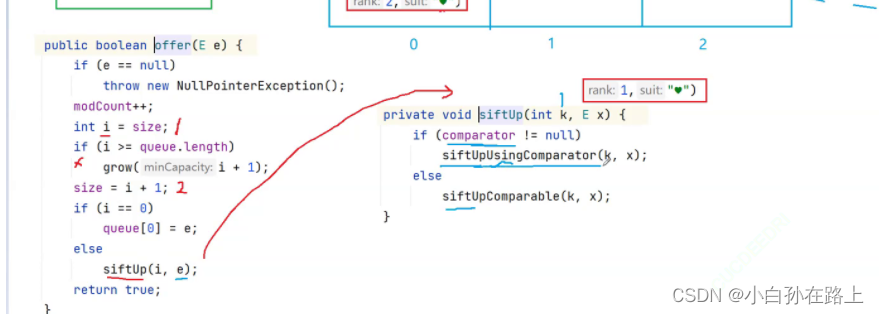
那么向上调整的时候就直接jinelse语句
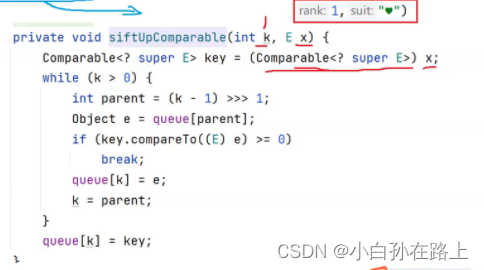
这里就会发现.e会被强转为Comparable类型
所以如果card不实现COMPARABLE接口就会强转不过来会报错
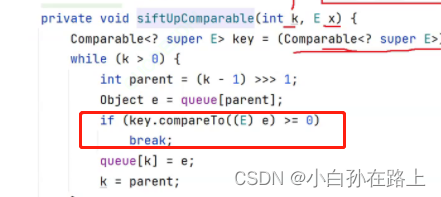
这里就调用Card的compaeto方法所以就算实现接口不重写也不可以
如果第二个就是比第一个大,就不需要交换(因为底层就是个小堆)
但是如果比他小,就需要往下走,交换,进行循环
那如果怎么样实现大堆呢
就改变CARD类本身的comparto方法,让前面的大于后面的大于0



3.Comparator比较器比较
实现一个ccomparator比较器
用户自定义比较器类,实现Comparator接口
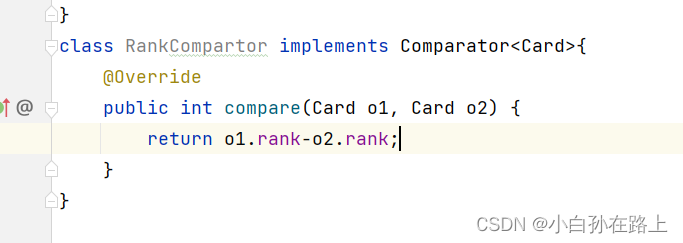
但是我们要用PriorityQueue
来进行比较,除了之前的比较方法

还有第一种,第一种如何实现
打开源码可以发现

构造方法默认是null,所以我们得穿一个比较器


先构造一个比较器,然后再构建队列的时候,放进去
4.总结

5.将优先级队列变成大根堆






![[附源码]计算机毕业设计springboot基于web的建设科技项目申报管理系统](https://img-blog.csdnimg.cn/ba5088ffeb8e4a89aee8264690550c43.png)