🎉🎉🎉点进来你就是我的人了
博主主页：🙈🙈🙈戳一戳,欢迎大佬指点!

欢迎志同道合的朋友一起加油喔🤺🤺🤺

---

目录

一、选择题

二、编程题

  🔥年终奖

  🔥迷宫问题

---

---

一、选择题

1、将N条长度均为M的有序链表进行合并，合并以后的链表也保持有序，时间复杂度为()?
A O(N * M * logN)
B O(NM)
C O(N)
D O(M)
正确答案： A
参考答案：
1.建立一个长度为N的最大/最小堆
将这N条链表的第一个元素拿出来建立最小堆，时间复杂度为O(N)
2.依次从最小堆中取出元素(堆顶)，此时堆顶就是当前集合的最小值，将链表的其他元素放入堆中。调整堆的时间复杂度(siftDown-O(logN))，总共还需要入堆的元素个数，O(NMloqN)
3.总共:建堆+不断调整堆(不断取出堆顶元素)O(N)+O(NM*loqN)
2、下设栈S的初始状态为空，元素a,b,c,d,e,f依次入栈S，出栈的序列为b,d,c,f,e,a则栈S的容量至少为（）
A 6
B 5
C 4
D 3
正确答案： D
3、大小为MAX的循环队列中，f为当前对头元素位置，r为当前队尾元素位置(最后一个元素的位置)，则任意时刻，队列中的元素个数为
A r-f
B (r-f+MAX+1)%MAX
C r-f+1
D (r-f+MAX)%MAX
正确答案： B
数组长度和最多存放的元素个数(MAX)
数组长度 =MAX-1(判断队列满，浪费一个空间)
4、HASH 函数冲突处理方式不包括以下哪一项：
A 开放定址法
B 链地址法
C 插入排序法
D 公共溢出区法
正确答案： C
5、若一棵二叉树具有12个度为2的结点，6个度为1的结点，则度为0的结点个数是（）。
A 10
B 11
C 13
D 不确定
正确答案： C
度为2的节点个数+1=度为0的结点个数(叶子结点)度为0的结点+度为1的结点+度为2的结点 =总结点个数边长=总节点个数-1。
6、（）二叉排序树可以得到一个从小到大的有序序列。
A 先序遍历
B 中序遍历
C 后序遍
D 层次遍历
正确答案： B
7、已知小根堆为8,15,10,21,34,16,12，删除关键字 8 之后需重建堆，在此过程中，关键字之间的比较次数是（） 。
A 1
B 2
C 3
D 4
正确答案：C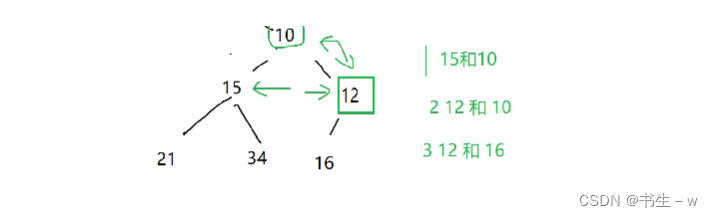

 8、已知某个哈希表的n个关键字具有相同的哈希值，如果使用二次探测再散列法将这n个关键字存入哈希表，至少要进行____次探测。
A n-1
B n
C n+1
D n(n+1)
E n(n+1)/2
F 1+n(n+1)/2
正确答案： E
n个关键字入哈希表的过程
第一个元素入哈希表,1
第二个元素入哈希表,2
第三个元素入哈希表,3
…
第N个元素入哈希表，n
1+2+3+…+n=(1+n)*n/2
9、下列选项中，不可能是快速排序第2趟排序结果的是 （）
A 2,3,5,4,6,7,9
B 2,7,5,6,4,3,9
C 3,2,5,4,7,6,9
D 4,2,3,5,7,6,9
正确答案： C
每进行一次快排，标定点一定处在最终位置
进行了两次快排，则至少有两个元素到达最终位置。
10、堆排序平均执行的时间复杂度和需要附加的存储空间复杂度分别是（）
A O(N2)和O(1)
B O(Nlog2N)和O(1)
C O(Nlog2N)和O(N)
D O(N2)和O(N)
正确答案： B

---

二、编程题

    🔥年终奖

  年终奖_牛客题霸_牛客网

 【解题思路】：
本题需要使用动态规划求解。
定义f(i,j)表示从左上角走到坐标(i，j)处能获得的最大奖励。
搜索所有从左上角走到右下角的路径，找到最优路径。
f(i,j)分三种情况：
第一列：f(i, 0) = f(i-1, 0) + board(i, 0)
第一行：f(0,j) = f(0, j - 1) + b(0, j)
其它位置：f(i, j) = max{f(i-1, j), f(i, j - 1)} + board(i, j)
最后返回右下角的值。

import java.util.*;
public class Bonus {
    public int getMost(int[][] board) {
       int row = board.length;
        int col = board[0].length;
        //处理第一行
        for(int i = 1; i < col; ++i){
            board[0][i] += board[0][i - 1];
        }
        //处理第一列
        for(int i = 1; i < row; ++i){
            board[i][0] += board[i - 1][0];
        }
        //处理剩余位置
        for(int i = 1; i < row; ++i){
            for(int j = 1; j < col; ++j){
            //F(i, j) = max(F(i - 1, j), F(i, j - 1)) + board[i][j]
                board[i][j] += Math.max(board[i - 1][j], board[i][j - 1]);
            }
        }
        return board[row - 1][col - 1];
    }
}

🔥迷宫问题

迷宫问题_牛客题霸_牛客网

 【解题思路】：
本题可用回溯法求解 具体步骤为：

1. 首先将当前点加入路径，并设置为已走
2. 判断当前点是否为出口，是则输出路径，保存结果；跳转到4
3. 依次判断当前点的上、下、左、右四个点是否可走，如果可走则递归走该点
4. 当前点推出路径，设置为可走

import java.util.*;
import java.io.*;
class Node{
    int x;
    int y;
    public Node(int x, int y){
        this.x = x;
        this.y = y;
    }
}
public class Main{
    public static void main(String[] args) throws Exception{
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        String str;
         while((str = reader.readLine()) != null){
                String[] arr = str.split(" ");
                int row = Integer.parseInt(arr[0]);
                int col = Integer.parseInt(arr[1]);
                //创建迷宫矩阵
                int[][] mat = new int[row][col];
                //读入迷宫数据
                for(int i = 0; i < row; ++i){
                    str = reader.readLine();
                    arr = str.split(" ");
                    for(int j = 0; j < col; ++j){
                        mat[i][j] = Integer.parseInt(arr[j]);
                    }
                }
                //搜索最短路径
                ArrayList<Node> path = new ArrayList<>();
                ArrayList<Node> minPath = new ArrayList<>();
                int[][] book = new int[row][col];
                getMinPath(mat, row, col, 0, 0, book, path, minPath);
                //打印最短路径
                for(Node n : minPath){
                    System.out.println("(" + n.x + "," + n.y + ")");
                }
            }
    }
    //mat: 迷宫矩阵, row, col
    //x, y: 当前位置
    //book: 标记矩阵，标记当前位置是否走过
    //path: 保存当前路径的每一个位置
    //minPath: 保存最短路径
    public static void getMinPath(int[][] mat, int row, int col,int x, int y, int[][] book, ArrayList<Node> path, ArrayList<Node> minPath){
        //判断(x,y): 是否越界，是否走过，是否有障碍
        if(x < 0 || x >= row || y < 0 || y >= col|| book[x][y] == 1 || mat[x][y] == 1){
            return;
        }
            //把当前位置存入路径中
            path.add(new Node(x,y));
            //标记当前位置
            book[x][y] = 1;
            //判断当前位置是否为出口
        if(x == row - 1 && y == col - 1){
            //一条新的路径产生
            //判断是否为更短的路径
            if(minPath.isEmpty() || path.size() < minPath.size()){
            //更新更短路径
                minPath.clear();
                for(Node n : path){
                minPath.add(n);
                }
            }
        }
        //继续搜索(x,y)的上下左右四个方向
        getMinPath(mat, row, col, x + 1, y, book, path, minPath);
        getMinPath(mat, row, col, x - 1, y, book, path, minPath);
        getMinPath(mat, row, col, x, y - 1, book, path, minPath);
        getMinPath(mat, row, col, x, y + 1, book, path, minPath);
        //把当前位置从路径中删除，寻找新的路径
        path.remove(path.size() - 1);
        book[x][y] = 0;
    }
}