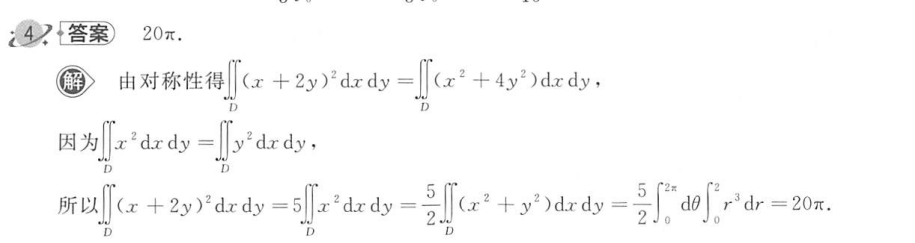一般对称性
一元函数的对称性
几何意义是所围图形的面积绝对值
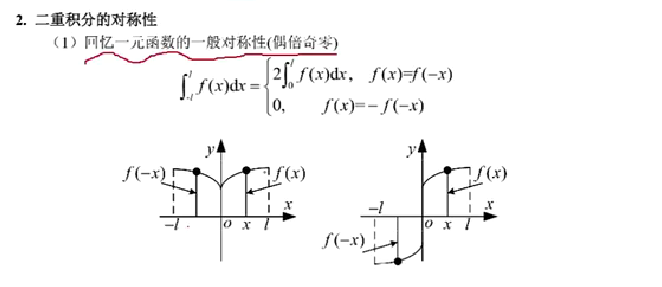
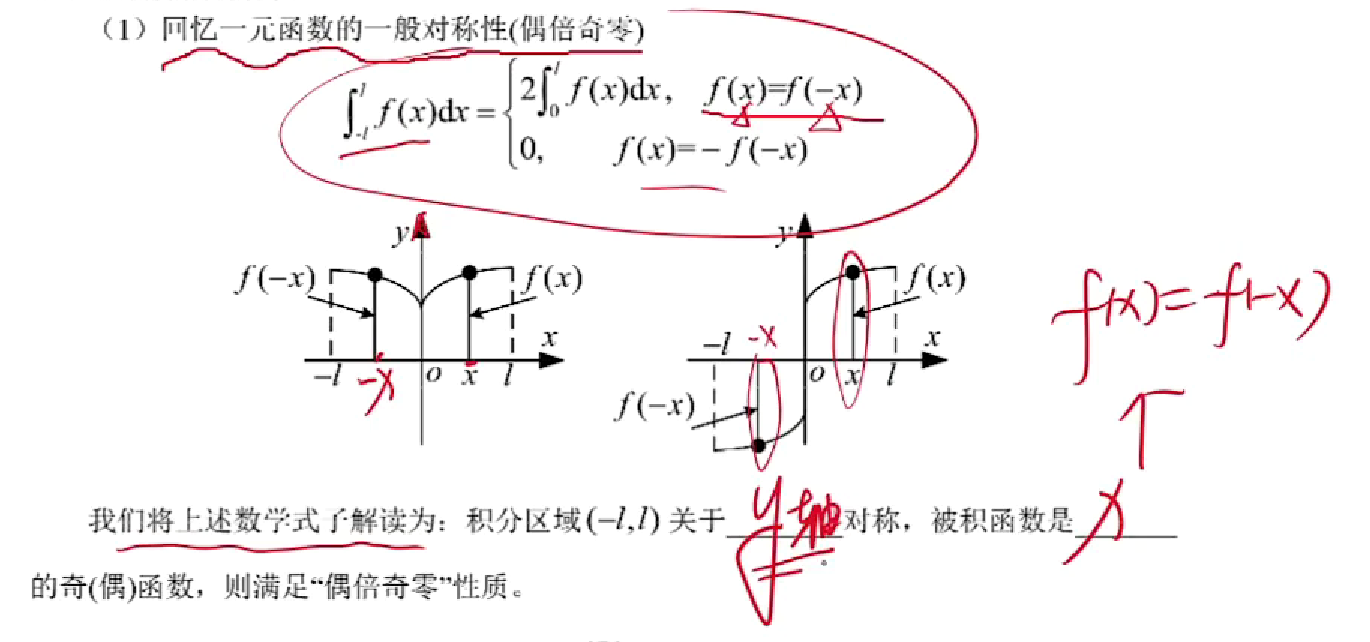
【注】使用对称性的时候,首先抓积分区域关于哪个轴对称,其次抓被积函数是为另一轴的奇(偶函数)。
二元函数的对称性(奇偶性)
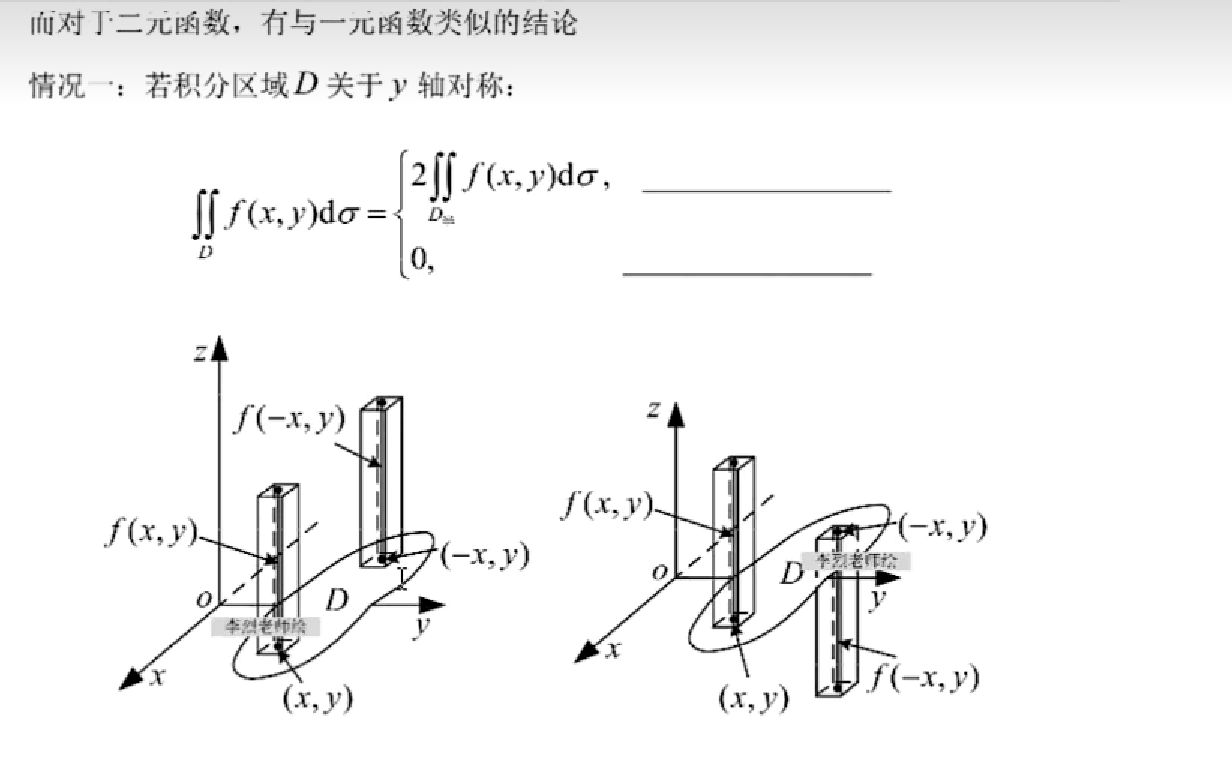
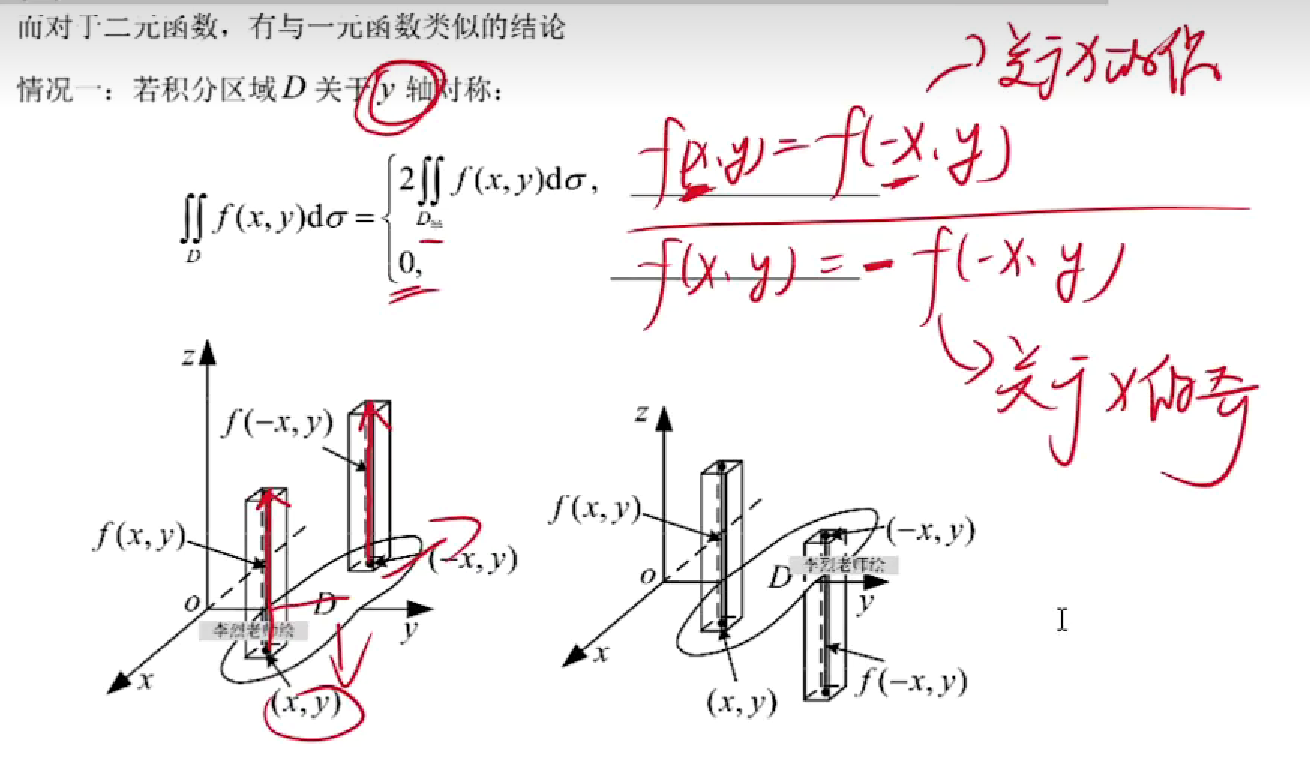

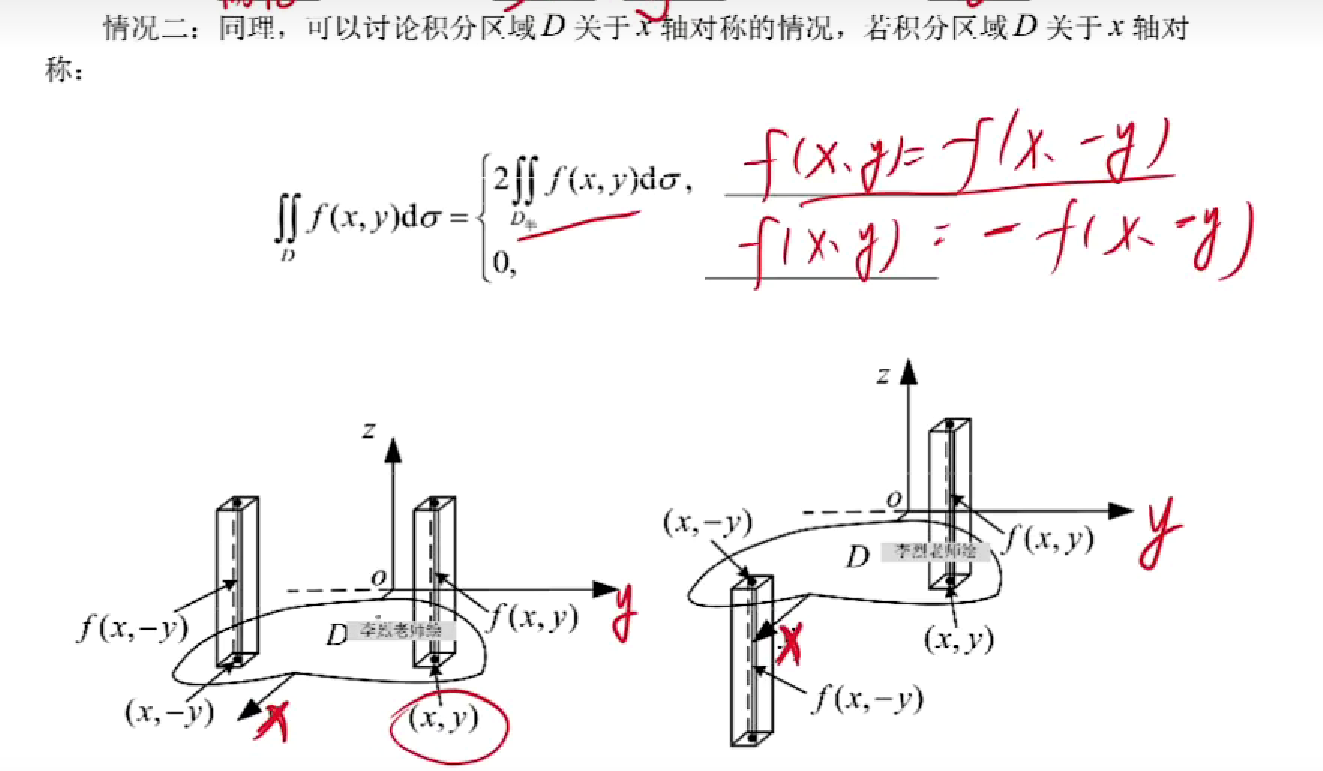
【注】在一般对称性中,(x,y)关于x,y的奇偶性只能关于一个变量面言,不能两个变量混在起讨论。
【注】1.二重积分计算时,一定要先观察被积函数的
积分区间是否具有对称性,利用一般对称性(偶倍奇零)和轮换对称性化简积分是顺利解题的先诀条件。如果积分区域不具有明显的对称性,可以考虑分割积分域,使得分制后的各积分区域只有对称性,然后在各区域上分别积分,2.使用一般对称性时,还需要被积函数具有奇偶性,如果被积函数不具有明显的奇偶性,可以考虑拆分被积函数分别积分。
例题
A


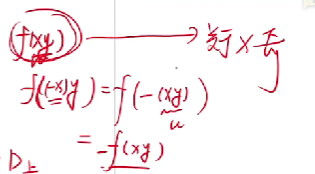

B

C
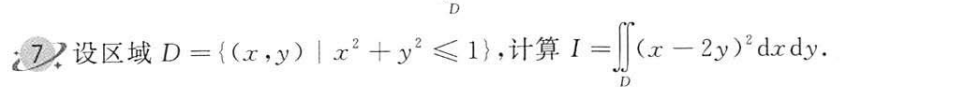

D
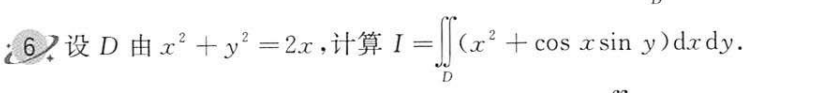

轮换对称性

只要关于积分区域 x=y 对称就有这个结论

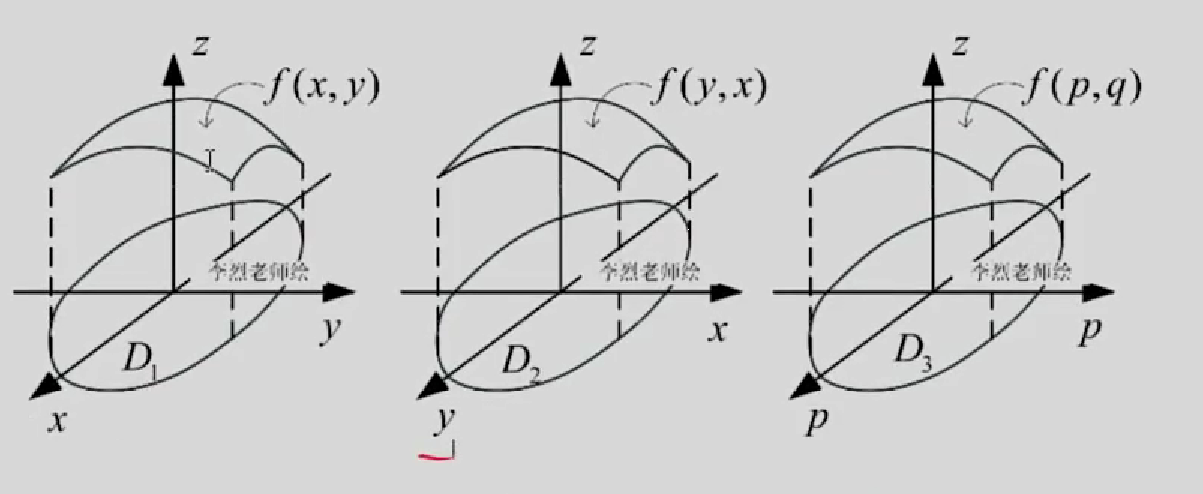

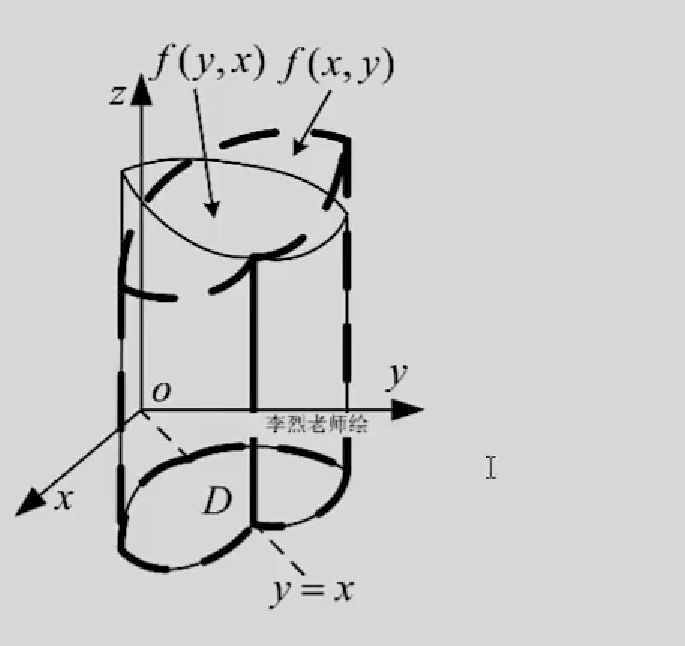

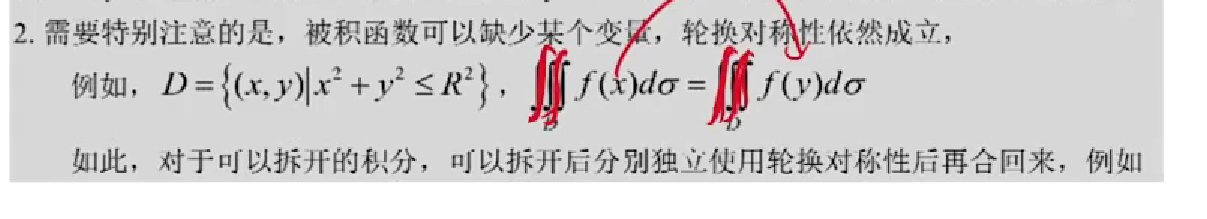
例题:
A 单变量的轮转对称

B 单变量的轮转对称
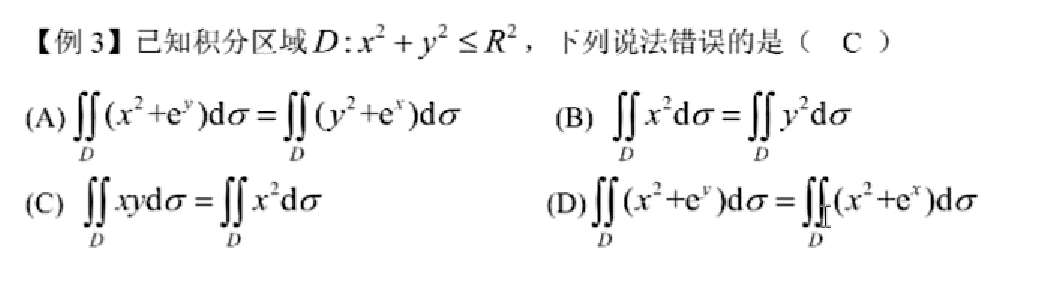
A, D选项就是分别拆开 再对 e的y次方进行轮换对称的
B 直接进行轮换对称,只是在原被积函数中没有y ,故结果就像 只是把 x 替换为 y样,实际上是,x-> y, y ->x。
C 双变量的轮转对称
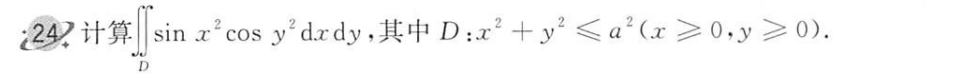
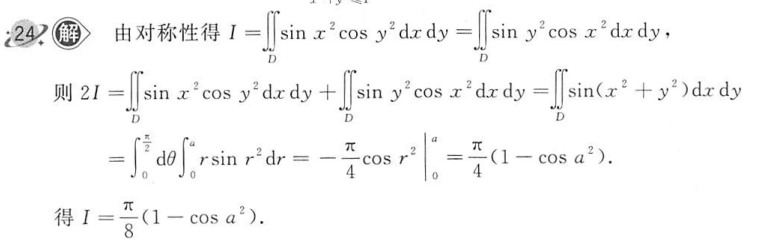
D 单变量的轮转对称
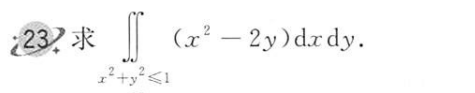
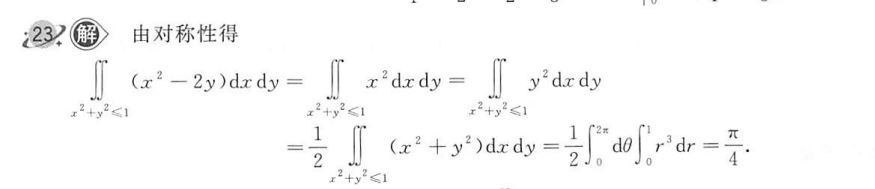
(因为是关于xy轴 对称, 故关于 被积函数-2y关于 y 为奇函数,为0)
E 双变量的轮转对称
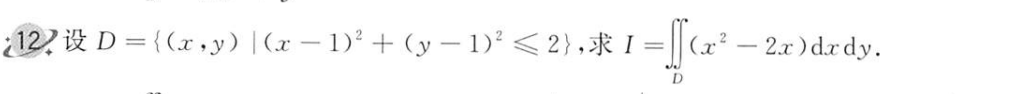
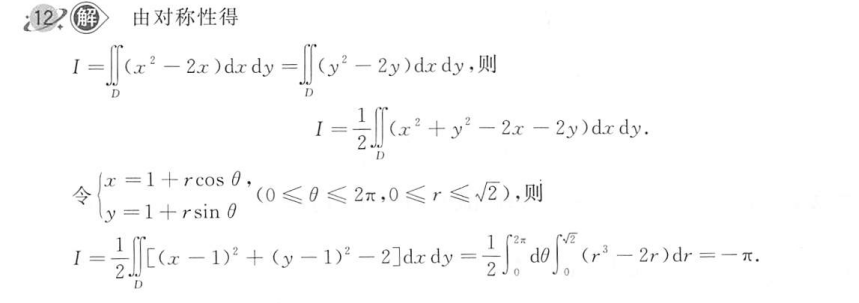
F 双变量的轮转对称
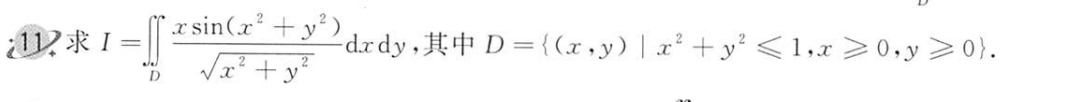
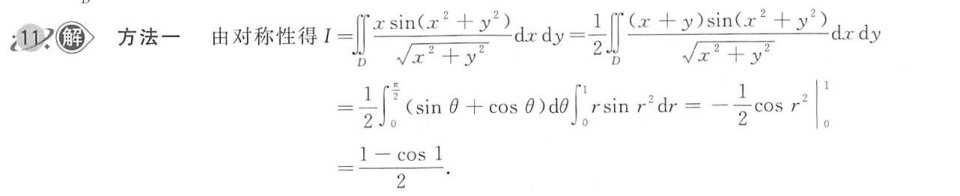
G 双变量的轮转对称
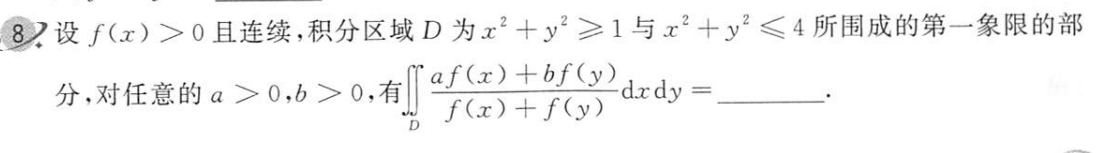
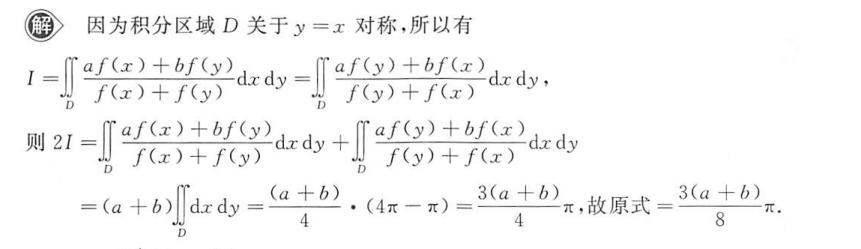
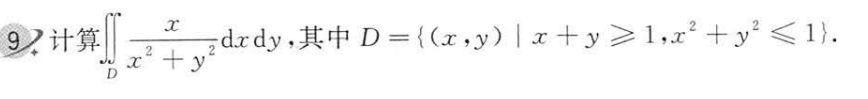
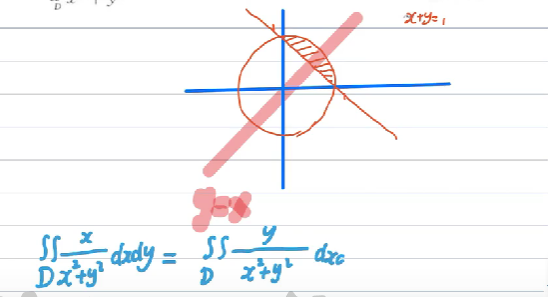
H 单变量的轮转对称性
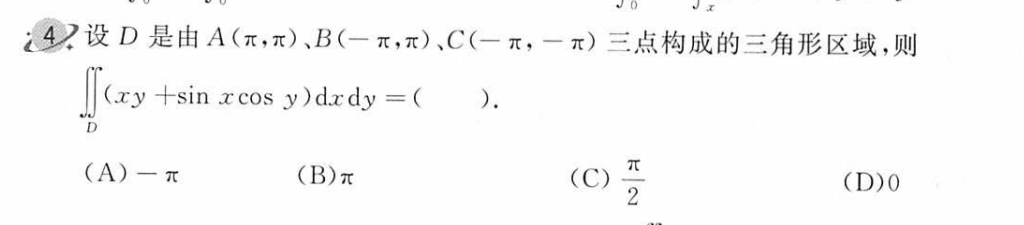
…(img-v5w41SNE-1682922146810)]
[外链图片转存中…(img-SE4zfr0Z-1682922146811)]
[外链图片转存中…(img-HAgT6aAs-1682922146812)]
[外链图片转存中…(img-1idCpxjJ-1682922146812)]
H 单变量的轮转对称性
[外链图片转存中…(img-l39ZYIsC-1682922146813)]