问题引入

在构造编译器的Scanner时，常见的解决方法是使用自动机技术。从文法构造出的DFA的状态数过多会影响编译器的性能。DFA中有一些状态本质上是等价的，我们需要一种自动化算法用于最小化DFA。

算法介绍

常见的DFA最小化算法有三种，分别是Moore算法、Hopcroft算法和Brzozowski算法。
很多教材，包括我们学校使用的教材（龙书）中给出的方法都是Moore算法。

Hopcroft算法

话不多说，先上伪代码：

符号解释

先解释一下这里使用的一些数据结构

Partition

当前等价类集合。最早是两个等价类，分别是输入DFA中的接收状态集合和非接收状态集合。

NextP

在一次迭代之后更新之后的等价类集合。NextP的功能是暂存变化的等价类，这能起到一个同步更新划分的作用。

Worklist

这个比较有意思。它维护的是一个“可能会导致当前等价类需要进一步划分”的等价类列表。（请记住这个定义）举个例子，考虑等价类{A, B}和{C, D}。DFA中有边A->C和B->D，这时{C, D}就导致了{A, B}需要进一步划分成{A}、{B}。在每一轮迭代中，会从Worklist中选出一个等价类s，然后考察每个当前等价类（Partition）中的集合p，看s是否会导致p需要进一步划分。

细节解释

现在来分步看这段伪代码。
首先初始化了三个核心数据结构，这步比较好看懂。D即为DFA的状态集，DA即为DFA的接收状态集。

紧接着开始迭代。迭代的结束条件是Worklist不为空，迭代条件的设置也很有意思，Worklist是“可能会导致当前等价类需要进一步划分”的等价类列表，当这样的等价类不存在，那么自然就意味着当前等价类已经不需要进一步划分了，那么自然最小化的目标达成，算法结束。

在迭代的循环体内，首先从Worklist中挑出一个集合s，然后生成了一个状态集合Image。这里应该是叫“原像”。Image包含的状态就是能经过c字符变迁到s集合中任意一个状态的状态。
举个例子，s集合中有一个状态A，DFA中有边D->A@c，那么D就是Image中的一个状态。

紧接着，开始考察当前等价类（Partition）中的每一个等价类q，看它是否会因状态s而需要进一步划分。考察方式是计算q和Image的交集和差集，如果均不为空，那么代表发生了这样的情况：q中只有一部分状态经过c变迁会到达s集合中的状态（交集不为空），而另一部分则会到达其他状态（差集不为空），这与等价类的定义：等价类的任一对状态对某个输入字符c下的行为应该相同，即变迁到同一个等价类不符。因此我们把p划分为交集和差集，然后更新Parttion和NextP。

Q:为什么要从Partition中移除q呢？
A:这是因为每一轮迭代都会考虑所有字符。每个等价类对于不同的字符可能有不同的划分方式，为了避免冲突，一轮迭代中q被一个字符划分后，就移除，下一轮迭代再加进来，以考虑其他字符对它的划分。

Q:为什么对Worklist的更新因q是否在Worklist中而不同？
A:前面提到过，Worklist维护的是一个“可能会导致当前等价类需要进一步划分”的等价类列表。
1.如果某个q不在Worklist中了，就代表对所有的等价类，对所有的输入字符，都不会因为q而需要进一步划分。进一步地讲，就是说对于任意一个等价类，对于里面所有的状态在任意一个字符下，变迁得到的状态要么全在q中要么全不在q中。然而这时候q被划分了，这对其他等价类是可能有影响的，见下图：

假设q被分割成了q1和q2某个等价类s在任意一个输入字符下变迁得到的状态集合，在q中的分布可能出现以下四种情况：
如果出现了2、3、4情况，那么这个等价类s就不会因为q而需要进一步划分。
如果出现了第一种情况，那么这个等价类s会因为q而需要进一步划分！读者可以自行想象，这时候不管是把q1加进Worklist还是把q2加进Worklist，都会让s被同样地划分！
那么自然就加比较小的。

2.如果这个q还在Worklist中，那么自然要把q1和q2都加进来。这是直觉上就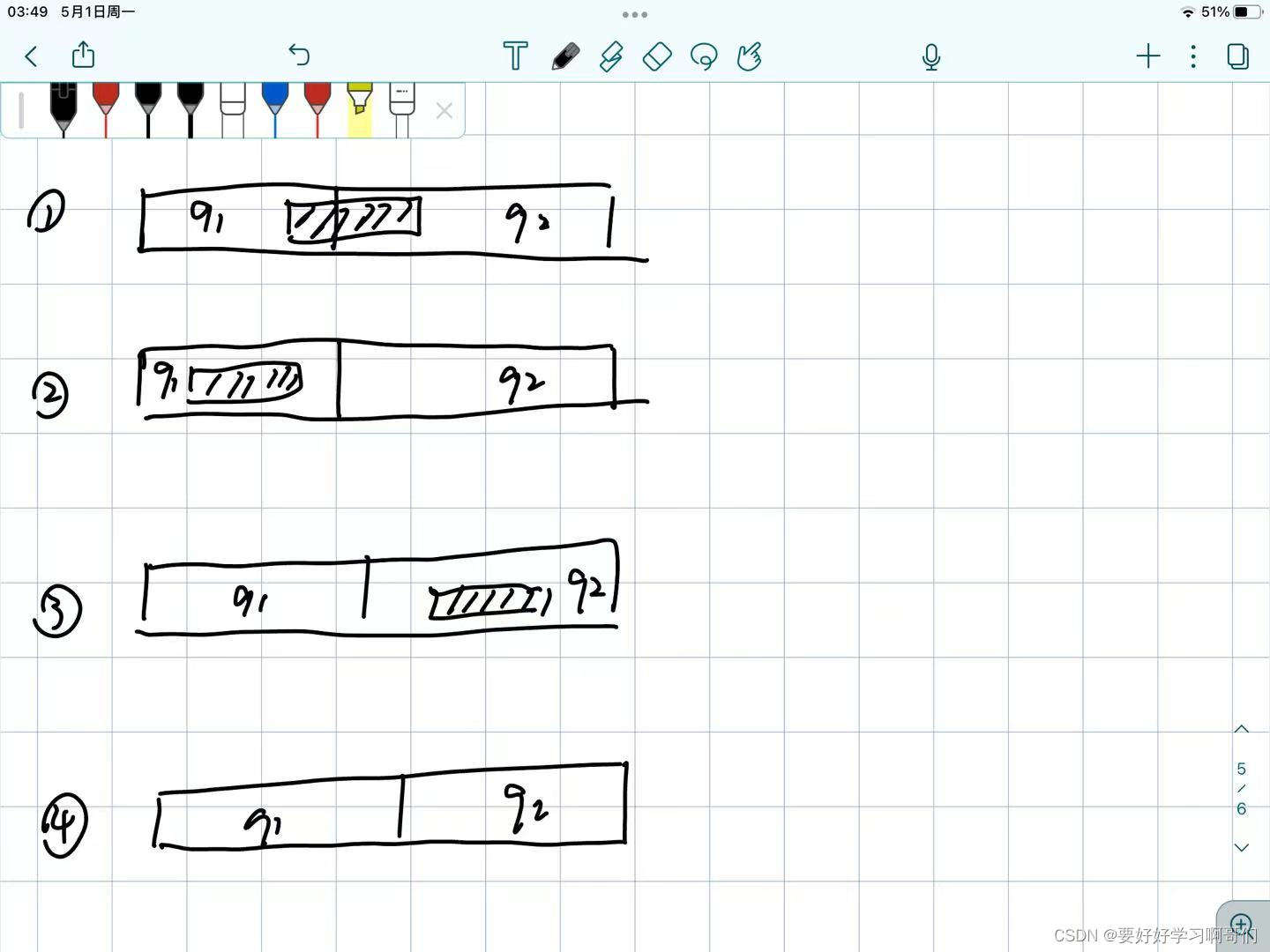
能理解的事情。

代码实现

坑，待填