343. 整数拆分(中等)



方法一:数学推导
思路
将数字 n 拆分为若干个数字之和,即 n = n1 + n2 + ... + na ,本道题等价于求解 max(n1 * n2 * ... * na) ,根据数学推导,可以得到两个结论:
- 当所有拆分出的数字相等时,乘积最大。
- 将数字 n 尽可能以因子 3 等分时,乘积最大。
详细推导过程可以参考 证书拆分:数学推导。
拆分规则
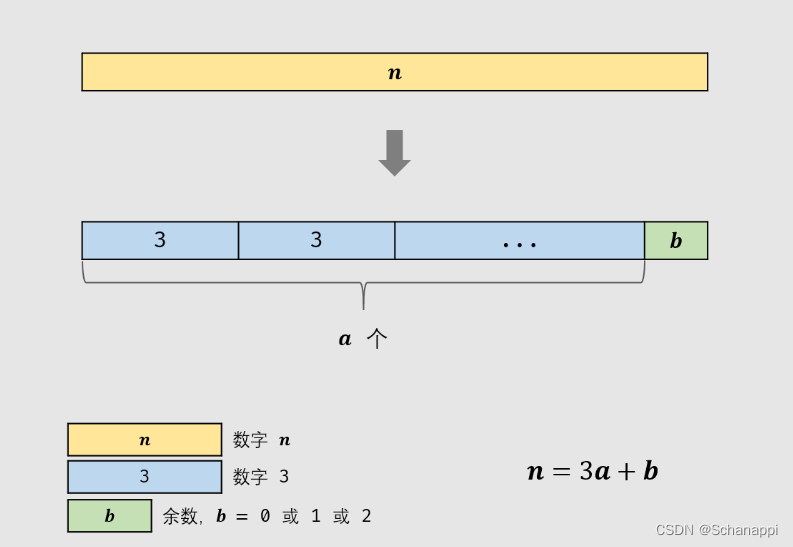
有了这两条推论后,我们就将数字尽可能拆成多个 3 ,显然余数有 0、1、2三种情形:
- 余数为 0:这是最好的情况,不需要继续拆分,即
n = 3 * k; - 余数为 1:由于任何数乘以 1 都得到它本身,所以这是最坏情况,我们应该避免这种情况的出现,将其中一份 3+1 替换成 2+2 。
- 余数为 2:应该保留,不需要继续拆分成 1+1。
算法过程
- 如果
n<=3,由于题目要求必须拆分,因此肯定会拆分出一个 1,所以返回 n-1 。 - 如果
n>3,令 n 除以 3,可以得到商 a 和余数 b,即n = 3a + b,那么根据 b 的值会分为以下三种情况:- b = 0:返回
3^a; - b = 1:返回
3^(a-1) * 2 * 2; - b = 2:返回
3^a * 2。
- b = 0:返回
代码
class Solution {
public:
int integerBreak(int n) {
if(n <= 3) return n-1;
int a, b;
a = n / 3, b = n % 3;
if(b == 0) return pow(3, a);
else if(b == 1) return pow(3, a-1) * 4;
else return pow(3, a) * 2;
}
};
方法二:动态规划
思路
对于正整数 n,当 n >= 2 时,可以拆分成至少两个数的和。假设 x 是 n 拆出来的一个数,则 n-x 是剩余的部分。对于 n-x,有两种情况,一种是继续拆分成两个整数,另外一种是不继续拆分。
我们要求的是整数的最大乘积,所以就是选取两种情况的最大值。
状态定义
dp[i] 表示整数 i 的最大乘积。
状态转移方程
对于 dp[i] ,当 i>=2 时,假设拆分出的第一个整数是 j(1<= j < i),考虑两种情况:
- 将 i 拆分成 j 和 i-j ,且 i-j 可以继续拆分,此时的乘积为
j * dp[i-j]; - 将 i 拆分成 j 和 i-j ,且 i-j 不继续拆分,此时的乘积为
j * (i-j);
结果就是这两种情况的最大值,即 max(j * dp[i-j], j * (i-j)) 。
接下来考虑 j 值,j 的取值范围是 1 <= j < i,我们需要遍历所有 j 值,才能确定 dp[i] 的最大值,所以最终的状态转移方程为 dp[i] = max (1<=j<i){max(j * dp[i-j], j * (i-j))}
初始化
由于 1 不可以拆分,所以将 dp[1] 设置为 0 。
最终的返回结果
i 指的是正整数, 所以 dp[n] 就是最终的返回结果。
代码
class Solution {
public:
int integerBreak(int n) {
vector<int> dp(n+1, 0);
for(int i=2; i<=n; ++i){
for(int j=1; j<=i; ++j){
dp[i] = max(dp[i], j * max(i-j, dp[i-j]));
}
}
return dp[n];
}
};