你知道 AlphaFold2 吗?它真正解决了蛋白质三维结构预测的算法困境,堪称蛋白质界的 chat-GPT4,甚至它的意义不是 chat-GPT4 所能够匹敌的。它为世界疾病治疗药物开发以及探究生物生命之谜提供了通向天神的一条道路,未来是生物的世纪!AlphaFold2再登Nature,从业者都懵了:人类98.5%的蛋白质,全都被预测了一遍,现在,它已经公开了超两亿个蛋白质预测的三维结构,免费无偿提供,让我们感谢这一开源精神。
Alphafold 论文目录结构

1-3:介绍 Alphafold 的完成背景与其他模型的优势,以及取得的成就
4-5:介绍 Alphafold 的基本思路,预测核心部件(卷积神经网络)以及梯度程序的思路
6-10:介绍 Alphafold 第一阶段的输出——残基距离分布图,以及第二阶段梯度下降程序效果
11-14:说明了核心部件对应的卷积神经网络的输入特征说明,以及选择一些输入因素的原因
15-23:搭建蛋白质可微几何模型以及梯度下降处理的思路及其效果
23-27:Alphafold 对 T0986s2 蛋白质的预测,达到 TM 分数 0.8,展示了神经网络的输入如何影响最终的预测
残差
残差,是指实际观察值与回归估计值的差。残差分析就是通过残差所提供的信息,分析出数据的可靠性、周期性或其它干扰。残差图的分布趋势可以帮助判明所拟合的线性模型是否满足有关假设。残差有多种形式,上述为普通残差。为了更深入地研究某一自变量与因变量的关系,人们还引进了偏残差。以某种残差为纵坐标,其它变量为横坐标作散点图,即残差图,它是残差分析的重要方法之一。需分析具体情况,探索合适的校正方案,如非线性处理,引入新自变量,或考察误差是否有自相关性。
蛋白质相似性度量
蛋白质结构相似性通常通过RMSD(均方根偏差)分数、GDT(全局距离测试)分数和模板建模分数(TM-score)来衡量。
参考:蛋白质结构相似性与TM评分= 0.5有多显著? |生物信息学 |牛津学术 (oup.com)
RMSD
两种蛋白质结构的最佳叠加后所有等效原子对的均方根偏差(RMSD),然而,由于结构中的所有原子在计算中的权重相等,RMSD的主要缺点之一是,当RMSD值很大时,它对局部结构偏差比对全局拓扑更敏感。例如,即使核心部分的全局拓扑相同,如果尾部或某些环具有不同的方向,则两种蛋白质结构的RMSD可能很高;仅根据 RMSD 值,这无法与两个结构具有完全不同的拓扑的情况区分开来。很少使用到。
越高越不相似
TM-scores
TM评分是评估蛋白质结构拓扑相似性的指标。它使用Levitt-Gerstein权重计算所有残基对。TM 分数对全局拓扑比局部变化更敏感。此外,由于它采用蛋白质大小依赖性量表来归一化残基距离,因此随机蛋白质对的TM评分的大小与蛋白质大小无关
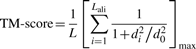
其中L是目标蛋白的长度,Lali是两种蛋白质中等效残基的数量。d i 是两个结构之间等效残基的第 i 对的距离,取决于叠加矩阵;“max”表示确定使公式(1)中的总和最大化的最佳叠加矩阵的过程。规模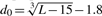 定义为标准化 TM 评分,即随机蛋白质对的平均 TM 评分的大小与蛋白质的大小无关。
定义为标准化 TM 评分,即随机蛋白质对的平均 TM 评分的大小与蛋白质的大小无关。
TM 分数保持在 (0, 1) 中,值越高表示相似性越强。
GDT 分数
GDT 分数被广泛用于社区范围的CASP和CAFASP实验,以评估蛋白质结构预测的建模准确性,随机结构对的GDT和MaxSub评分的大小与蛋白质长度具有幂律依赖性(Zhang和Skolnick,[2004](javascript:😉),这使得分数的绝对值意义不大。它还有一个缺点,即相关蛋白质的相似性在很大程度上取决于它们的长度
在大约 90 分的情况下,我们就可以认为从一串氨基酸序列转发成蛋白质折叠出的三维结构问题大部分已经得到解决,在 2020 年前的相关比赛中,从来没有超过 90,甚至是 60。GDT 分数意味着实际三维结构和生成的三维结构的全局距离分数。也可以说是预测结构和真实蛋白质结构相似度的度量值,如下:
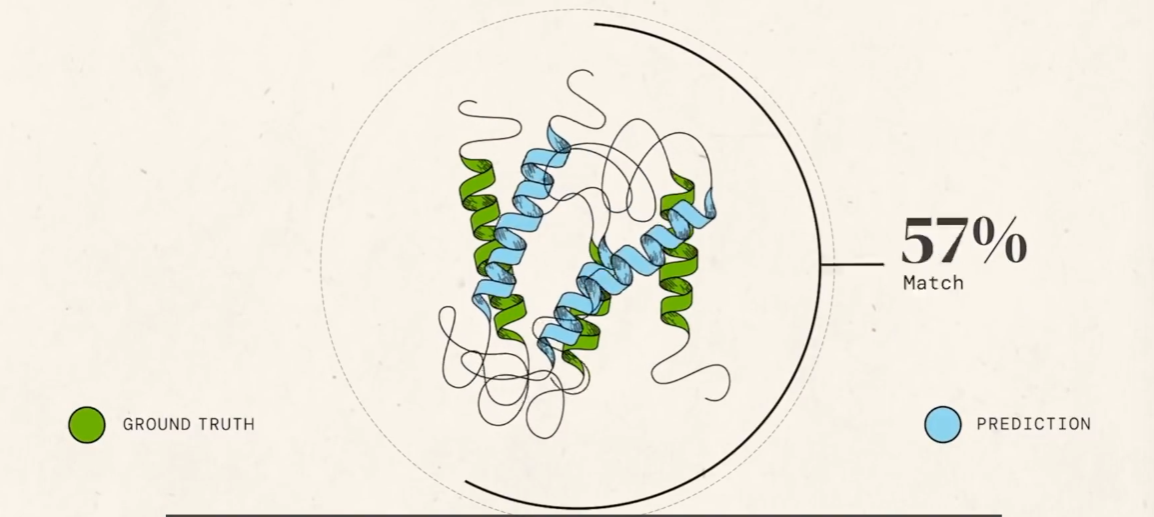
而使用 Alpha fold 测试 2018 年的数据,可以达到将近 60。
越高越相似。
lDDT分数(局部距离差测试)
基于刚体叠加的GDT评分无法解释多结构域蛋白中相对结构域取向的变化,需要分别比较每个结构域。
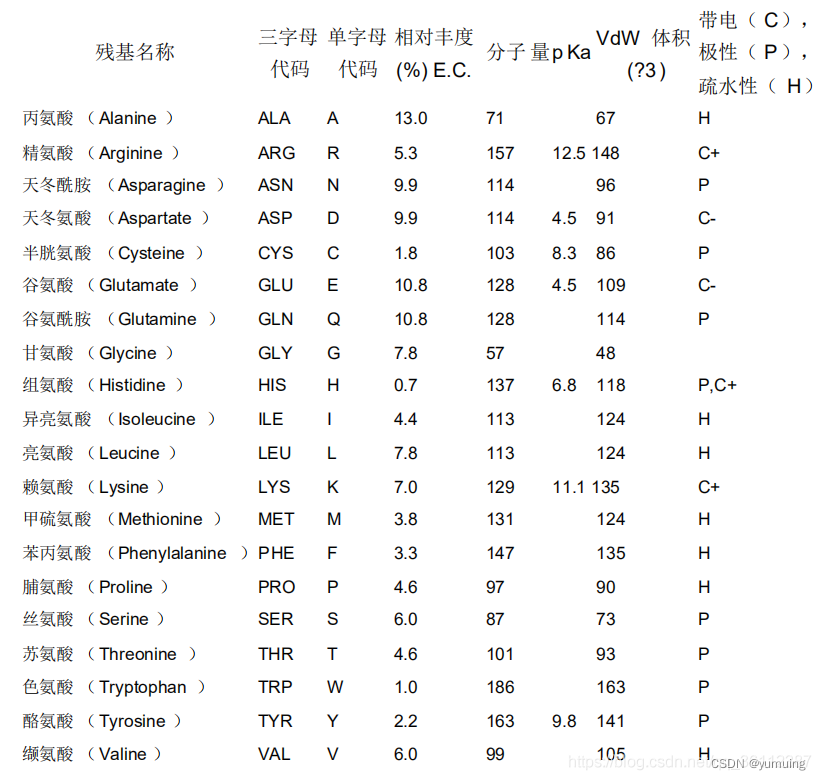
氨基酸缩写表
同源序列的共变异可推断哪些氨基酸残基是接触
同源序列(homologous sequences)
同源序列可以用**相似性(similarity)**来度量。注意,**同一性(identity)**指两条序列完全相同。
残基(Residue):
氨基酸之间的氨基和羧基脱水成键,氨基酸由于其部分基团参与了肽键的形成,剩余的结构部分则称氨基酸残基。也就是说在下图中,虚线框外的部分就是残基。

PDB 数据库
Protein Data Bank(以下简称,PDB,https://www1.rcsb.org/)是当今全世界最具公信力的蛋白质数据库之一,每一条蛋白质都有唯一标识,称为PDBID(类似每个人都有自己的身份证号,唯一标识),比如PDBID为1F88的蛋白质在PDB中如下:
蛋白质结构
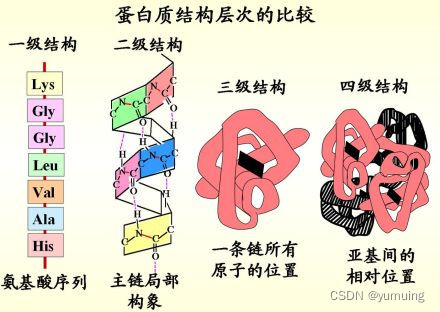
一级结构
蛋白质的1级结构指的是其氨基酸序列。在PDB中可以下到蛋白质的序列文件,如1F88的序列文件rcsb_pdb_1F88.fasta如下:
第一行记录了该蛋白的信息
第二行开始记录了该条蛋白质的序列,由一个个氨基酸构成。以这个1F88为例,序列中包含了348个氨基酸,说明1F88由348个氨基酸构成,所以1F88的长度为348。
3级结构就是空间结构。空间中每一个氨基酸集团由若干个原子构成。每一个原子都会有自己的唯一确定的三维坐标由(x,y,z)表示。
二级结构
蛋白质分子的二级结构(secondarystructure)通常是指蛋白质多肽链沿主链骨架方向的空间走向、规则性循环式排列,或某一段肽链的局部空间结构,即蛋白质的二级结构为肽链主链或一段肽链主链骨架原子的相对空间盘绕、折叠位置,它并不涉及氨基酸残基侧链的构象。
三级结构
蛋白质的三维结构
以1F88蛋白质为例,1F88的3级结构用文件1F88.pdb来描述。可在 pdb 数据库查看:
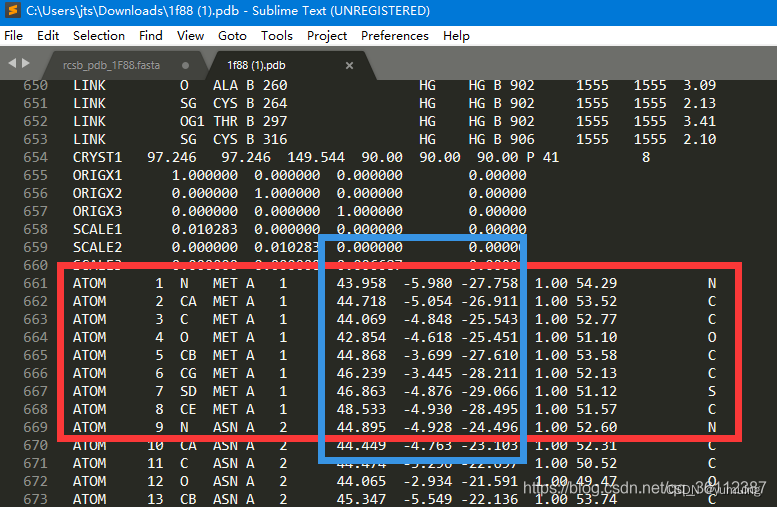
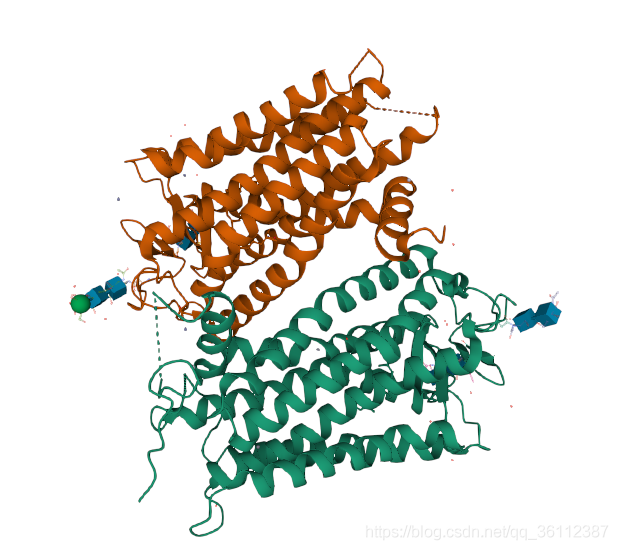
在知道了每个原子的三维坐标后,我们可以在坐标系中,把每一个原子都标记出来,这样就得到了蛋白质的三维结构的空间图,如1F88序列经过PDB文件的坐标解析后,用Pymol软件打开可以看到他的结构如下:
蛋白质残基接触
空间中2个氨基酸集团的Ca原子(一般用Ca原子来计算接触)的空间距离小于8Å(Å是距离单位)的时候,我们认定这两个氨基酸是处于接触contact状态。简单讲,就是通过距离来判断是否接触,推断是否能够发生反应。
怎么计算两个氨基酸是否存在接触,以 1f88 为例:
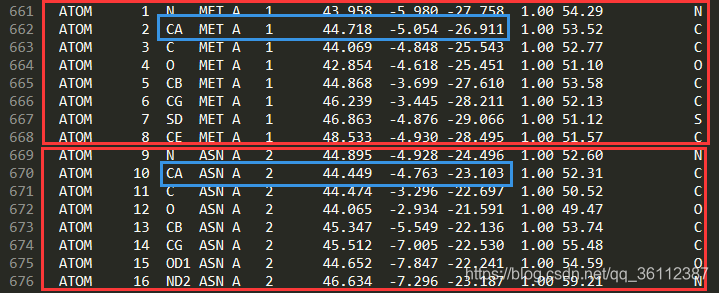
将pdb坐标文件中2个氨基酸集团中的CA原子分别取出来,然后用空间距离计算公式,计算一下结果便可以得知结果。
- MET_Ca的坐标为(x1,y1,z1)=44.718,-5.054,-26.911。ASN_Ca的坐标为(x2,y2,z2)=44.449,-4.763,-23.103。
- 代入空间中两点距离公式求这俩坐标之间的距离d。
得出结果为 d = 70.417122Å ,远远大于8Å的距离阈值要求。所以这俩氨基酸在空间中不接触。
CASP是二年一次的蛋白质结构预测竞赛,在CASP竞赛中,有专门的的一项就是接触预测竞赛。那么接触的意义是什么? 通俗的说,接触就是一种约束,有了约束,会决定蛋白质在空间中的空间结构(为什么蛋白质的螺旋往左边倾斜,不往右边倾,就是有一种约束在其中作用),而空间结构决定了蛋白质的功能。有了功能能为药物开发等提供研究基础等。所以对接触进行研究是极具意义的。
蛋白质接触矩阵
在知道什么是接触、接触如何计算之后,我们可以用矩阵的形式,来将一条蛋白质的接触信息展示出来。这个形式就是接触矩阵,或成接触图。
在接触矩阵M中,假设一条蛋白质序列的长度为L。那么这个接触矩阵的维度就是L*L,接触矩阵M是一个沿主对角线对称的矩阵。
矩阵中每一个元素的值要么是0要么是1。0表示不接触,1表示接触。我们可以用i和j来标识。
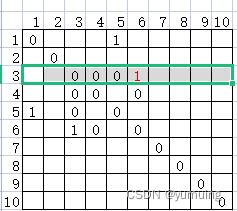
比如一条长度为10的蛋白质,他的接触矩阵M的维度就是10*10。
如那么第三行第六列为1。就表示该序列的第3个氨基酸与第6个氨基酸他们是接触的。
MSA:多序列对比
使用原因:
蛋白质的生成与 DNA 息息相关,而目前地球上绝大多数都是由同一个祖先进化而来的,特定功能的蛋白质在不同物种间也具有极大的结构相关性。而这种特定功能下的蛋白质序列的结构相似性,正是 MSA 多序列对比能够对蛋白质结构预测起一定作用的原因。当然,单序列直接预测蛋白质结构很美好,但存在很大的难度,那这样的话,为什么不利用各种数据库存储的序列信息与对应蛋白质结构关系的宝贵信息,将这个难度大大减低。
原理:
假设存在两个蛋白质,它们之间的作用对于生物极其重要,我们知道,两个蛋白质之间存在化学上的相互作用,意味着存在一定的结构维持这种作用,一旦其中一个蛋白质出现突变,为了维持这种作用,另外一个蛋白质也必须做出配合的突变,否则,生物就将面临死亡。并且,现存的所有生物都是来自于同一个祖先,在这样的情况下,依据统计学概率,提取特征,我们就可以判断相同某些氨基酸是否存在接触的可能。
如下图:我们可以预测位于黑球位置的氨基酸 S 与 氨基酸 H 存在接触的可能,氨基酸 F 与氨基酸 W 存在接触的可能。
其中,每一行氨基酸序列都是来自不同的生物。

Alphafol 从每个残基对的多序列对比中提取出了 484 个特征,还有部分能够明确表现出在 MSA 中缺失部分的特征:
- 1-hot amino acid type (21D)
- Profiles: PSI-BLAST (21D)
- HH280 blits profile (22D)
- non-gapped profile (21D)
- HHblits bias, HMM profile (30D)
- Potts model bias (22D)
- Deletion probability (1D)
- Frobe285 nius norm (1D)
- Gap matrix (1D)
这些特征作为预测残基距离的深度卷积神经网络的输入之一。
Alphaflod 思路
第一步:
基于目标氨基酸序列,在所有的数据库进行爬取,匹配出类似的在动物界中的相关物种的进化方向,再将这个 MSA 信息和一些额外的输入特征相结合,经过处理并重塑为二维数组并输入到深度残差卷积网络中。进而输出一个预测的蛋白质残基距离分布图。实际预测的不是蛋白质的残基距离分布,而是,每对残基之间的距离。
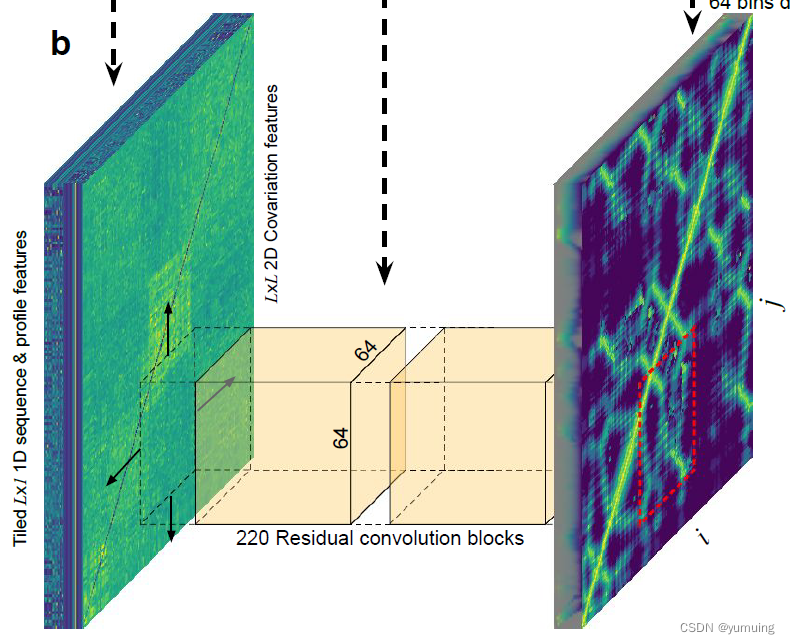
第二步:
结合不同残基间的扭转角度利用梯度下降法得出能够满足这样的残基距离的(不考虑物理力影响的)蛋白质的 3d 结构图。
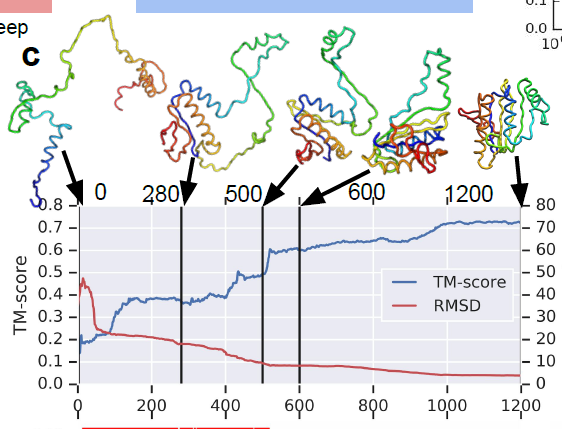
第三步
结合残基之间的物理力(范德华力)得出一个较为合理的蛋白质三维结构。
思路流程图如下:
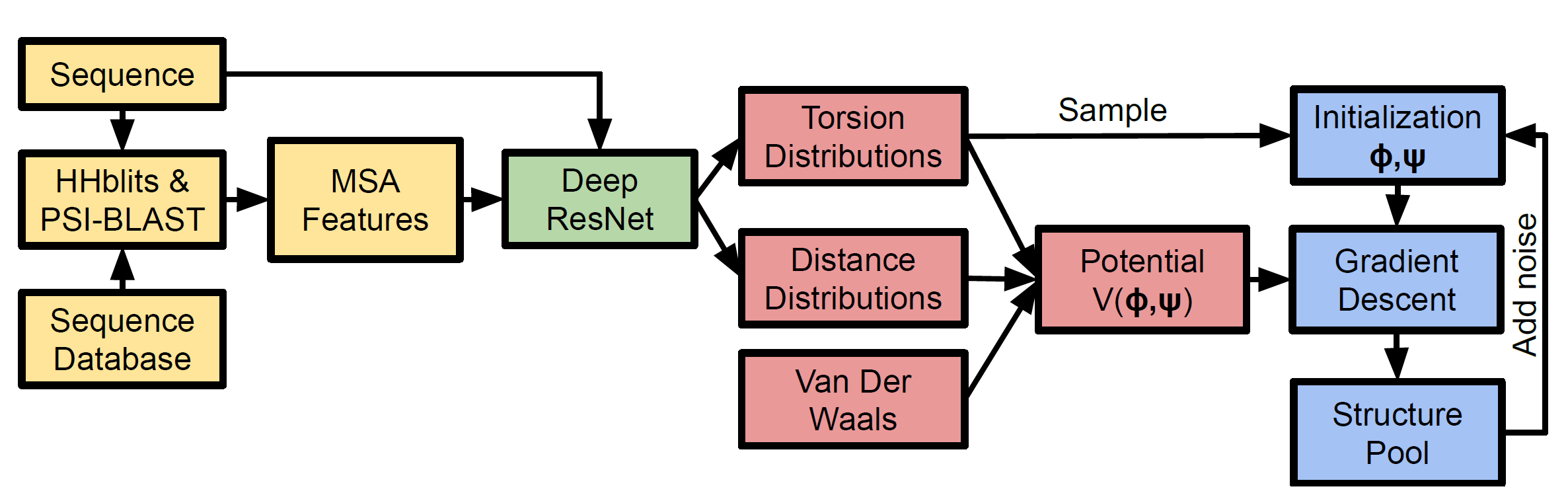
特征提取阶段(MSA 提取)用黄色表示,结构预测神经网络(蛋白质残基距离分布图)用绿色表示,潜在构造(基本骨架)用红色表示,结构实现用蓝色表示
蛋白质残基距离分布图
蛋白质每对残基之间的距离只是一个二维数组,里面每个数值都代表一个蛋白质 3d 结构中不同氨基酸之间的距离,比如在 i 行和 j 列的数字代表氨基酸 i 和氨基酸 j 的之间的距离。把这里的距离数字转换为颜色,即每个格子颜色深浅代表两个氨基酸距离。如下图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bBT4EC0S-1682786250119)(null)]
其中,SQET······代表氨基酸缩写字母。由于 i 到 j 与 j 到 i 的距离相等,所以蛋白质分布图会以主对角线为中心的对称矩阵。之所以使用蛋白质分布图来进行预测,正是因为无论蛋白质如何旋转、平移都不会改变蛋白质距离分布图。也就是说不同视角下的同一个蛋白质的残基距离分布图一致。从而,我们不用为了预测准确去把蛋白质以某个姿态进行对齐位置。
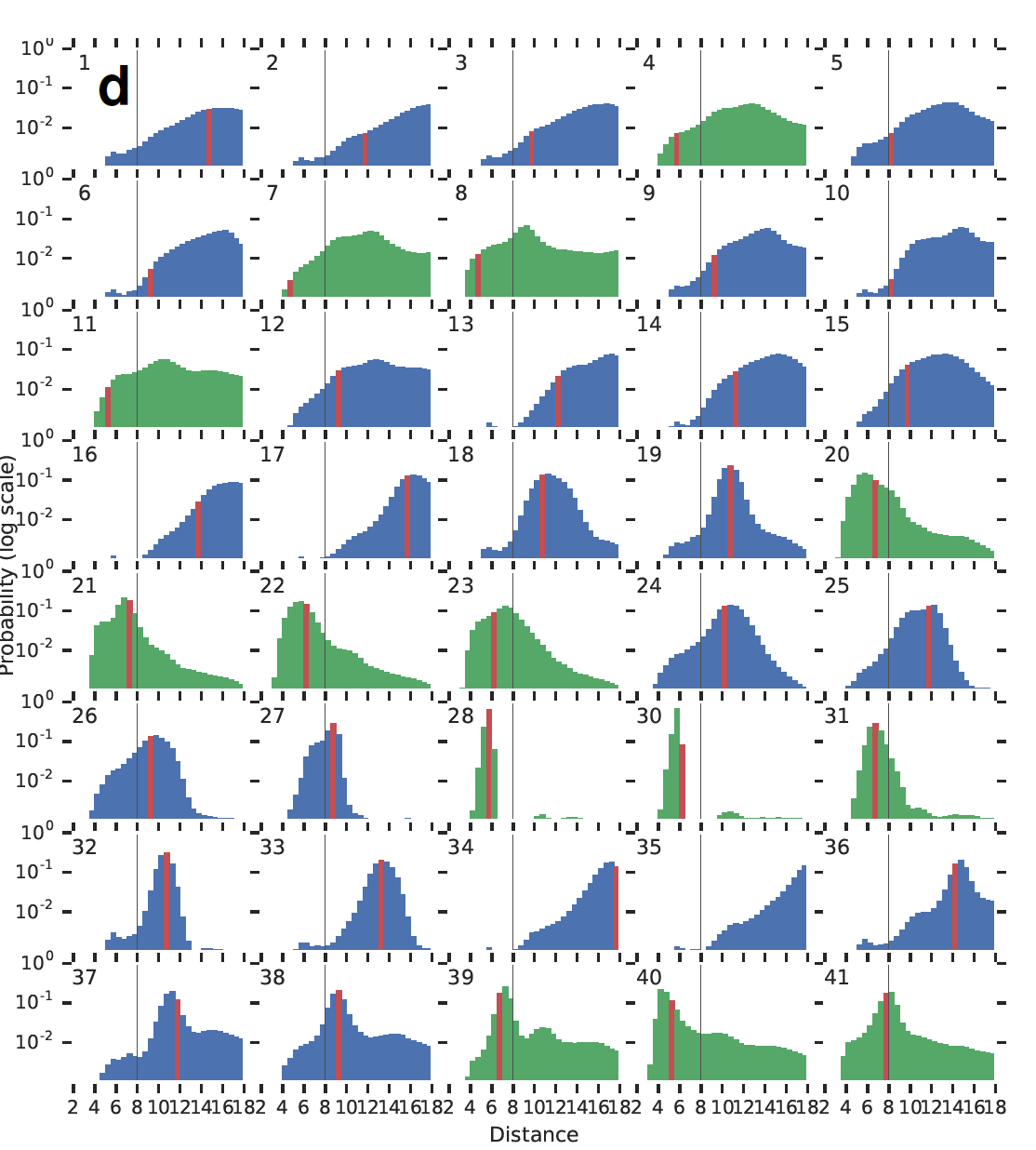
实际距离与预测距离的残差分布图
其中:
- 横轴是残基之间的距离值,竖轴是实际值与预测值的残差
- 绿色代表残基呈现接触状态的残差图,网格分布趋向于向右,红线在黑线左侧
- 蓝色代表残基呈现非接触状态的残差图,网格分布趋向于向左,红线在黑线右侧
- 黑色竖线代表 8 Å 距离的残基对,表示接不接触的距离,大于不接触,小于接触。
- 红色表示真实距离
以下为残基距离分布图中的第二十九位残基与其他残基的的残差分布图,可看出,第七副图和第八幅图的效果并不是很好,偏向中间。其中,最高置信度分布会最小变化,集中在红线附近,如第27、28、30、31幅图。距离应该也是在这个附近。
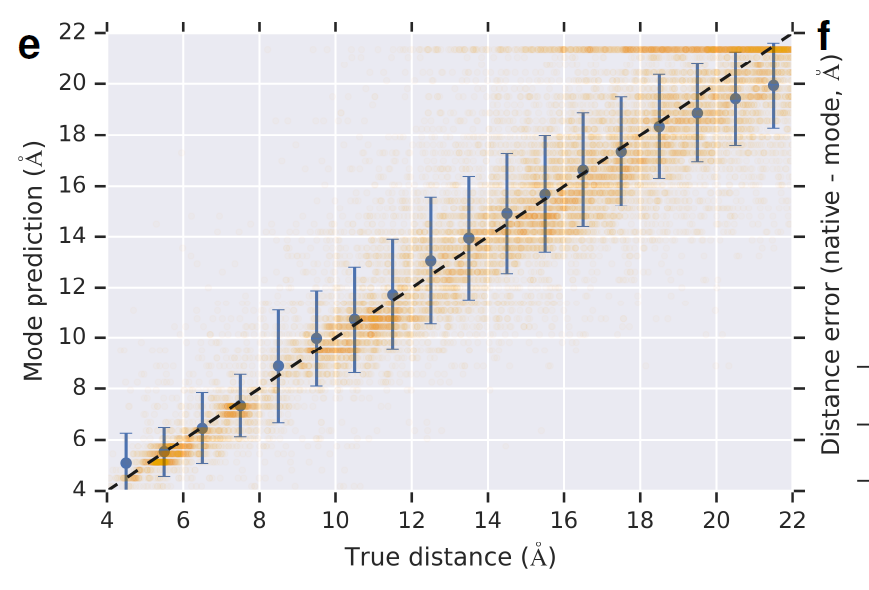
从下面这个图,我们可以看出模型预测的距离和实际距离很接近
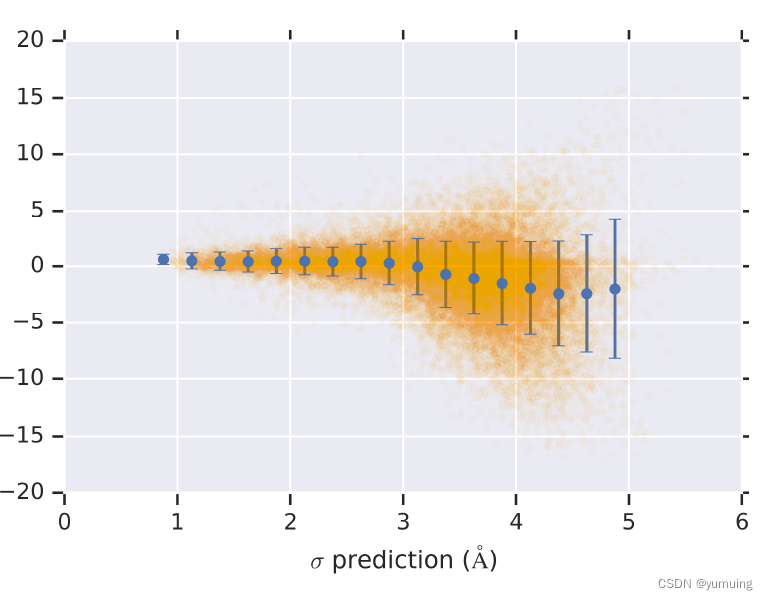
预测标准差平均值十分接近于 0 ,标准差越高,模型预测越不确定。
扭转角度的梯度计算法
利用残基距离预测分布图与偏移角度进行梯度下降法即可获得能够满足这样的残基距离的(不考虑物理力影响的)蛋白质的 3d 结构图。获得 3 d 结构图的方法为梯度下降法对这些变量进行处理。实际就是把每两个残基之间的 phi 和 psi 角度参数化,方法如下:
不同残基间的扭转角度(phi 和 psi 角度,也就是二级结构的基本构成)构建一个可微分的 蛋白质几何模型,该几何模型输出结果为 x = G ( φ , ψ ) x = G(φ, ψ) x=G(φ,ψ),进而获得 d i j = ∣ x i − x j ∣ d _{ij}= |x_i − x_j| dij=∣xi−xj∣ 再与与预测出来的残基距离进行相减的绝对值结果为损失函数,即 L = ∣ x − x ′ ∣ L = |x-x'| L=∣x−x′∣,由于可微,可得, d L d ψ {dL} \over {dψ} dψdL,通过改变角度,减低损失函数值,也就是梯度下降算法计算出残基之间的距离。
其中:
- φ, ψ 为 phi 和 psi 角度
- i、j 为氨基酸 i 和氨基酸 j
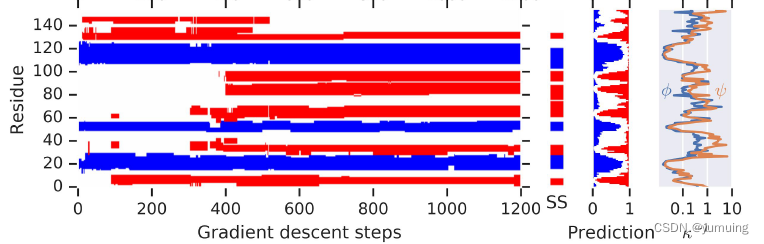
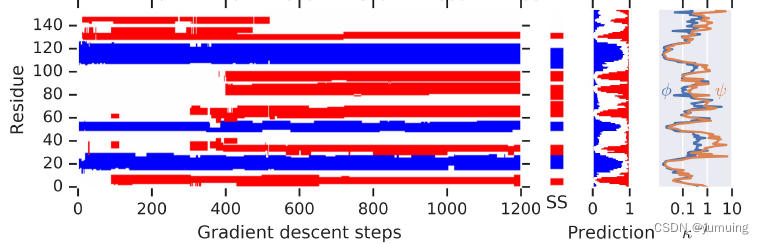
随着,梯度下降的一步步进行,到了 1200 步,就已经有不错的效果了。TM 分数在上升,RMSD 分数在下降。

并且,随着步数的增加,蛋白质间的螺旋结构与非落选结构的残差分布也越来越合理,当然,这里的螺旋与否的判别是通过某种启发式学习得到的。拥有橙色那个图是扭转角度的变化的残差分布图
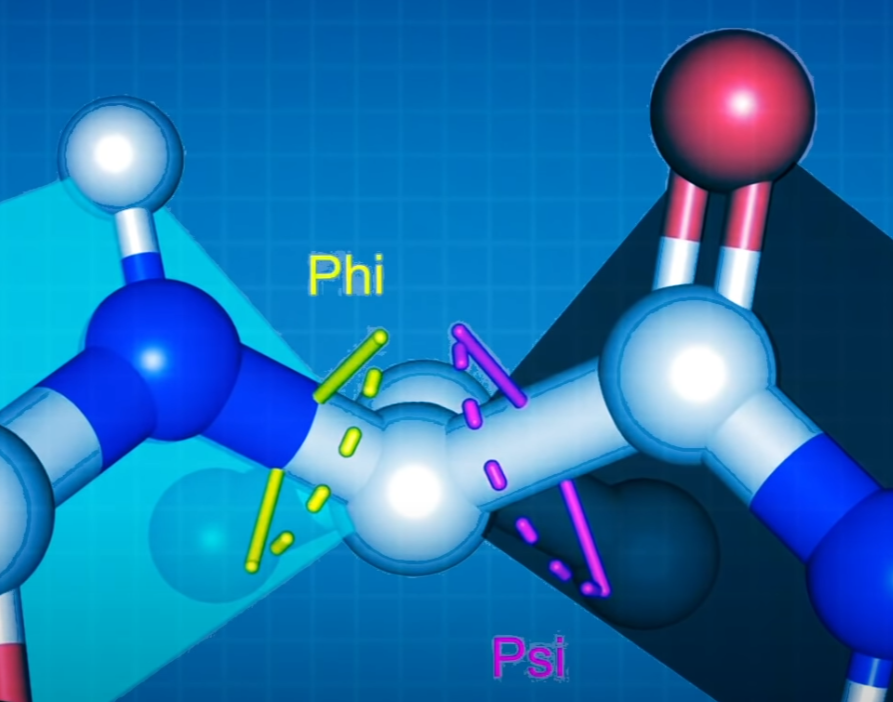
残基扭转角
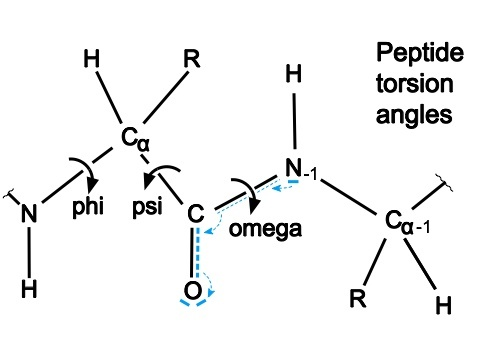
φ(phi)表示一个肽单位中α碳左边C-N键的旋转角度, ψ(psi)表示α碳右边C-C键的旋转角度。
注:蓝色是 N 原子,白色是 C 原子