贝叶斯与频率主义对蒙蒂霍尔问题的解
在定义概率时,通常有两种思想流派:贝叶斯主义和频率主义。前者将概率视为我们对事件发生的信念程度,而后者则将其视为事件发生的相对频率。这篇文章介绍了使用贝叶斯和频率主义方法来解决著名的蒙蒂霍尔问题。
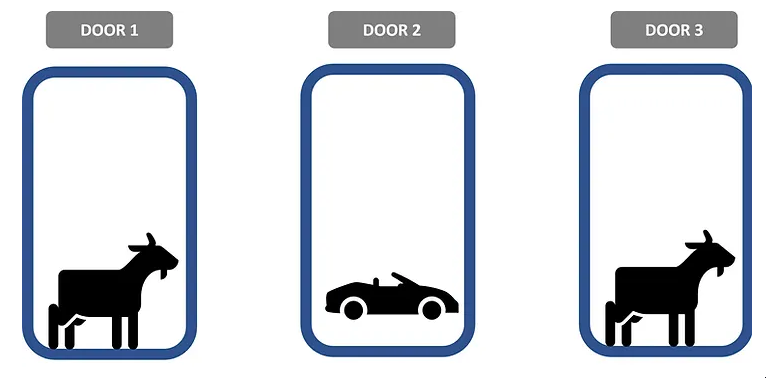
蒙蒂霍尔问题的插图
蒙蒂霍尔问题
我第一次偶然发现这个概率谜题是在电影21。这个谜题起源于一个古老的美国游戏节目Let's Make a Deal,并以主持人Monty Hall的名字命名。
基于维基百科,这在1990年给Marilyn vos Savant的“Ask Marilyn”专栏的一封信中广为人知:
假设你正在参加一个游戏节目,你可以选择三扇门:一扇门后面是一辆汽车;在其他人后面,是山羊。你选择一扇门,说1号,主持人,谁知道门后面是什么,打开另一扇门,说3号,里面有一只山羊。然后他对你说:“你想选择2号门吗?转换选择对您有利吗?
玛丽莲建议你应该坚持切换,因为这会使你赢得赛车的机会从 1/3 增加到 2/3。这个答案遭到了巨大的批评,因为人们直觉上倾向于认为,由于只剩下两扇门,那么两扇门后面的汽车的概率是 1/2。因此,无论您选择切换门,几率都是一样的。
在这篇博文中,我将演示如何使用贝叶斯或频率主义方法来回答这个悖论。
像贝叶斯一样思考
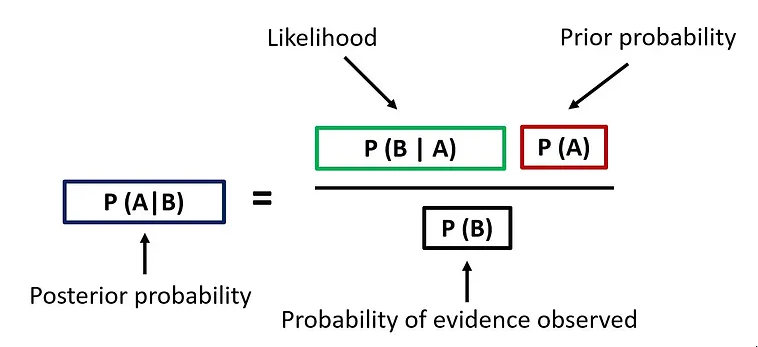
贝叶斯学派对概率采取主观方法,并以贝叶斯定理为基础。它基本上是由以下公式定义的条件概率概念。
简而言之,结果概率也称为后验概率是使用三个组成部分得出的:可能性、先验概率和观察证据的概率(0 到 1 之间的值)。
使用贝叶斯定理来解释为什么不同的人对相似经验证据的评价不同。
贝叶斯定理
在Monty Hall问题的背景下,我们有兴趣比较切换或坚持我们最初选择的门之间的概率,因为主机选择打开一扇后面有山羊的门。
使用上面提出的示例问题,假设门 3 已被揭示为山羊,汽车将在门 1(我们最初的选择)或门 2(如果我们选择切换)后面。
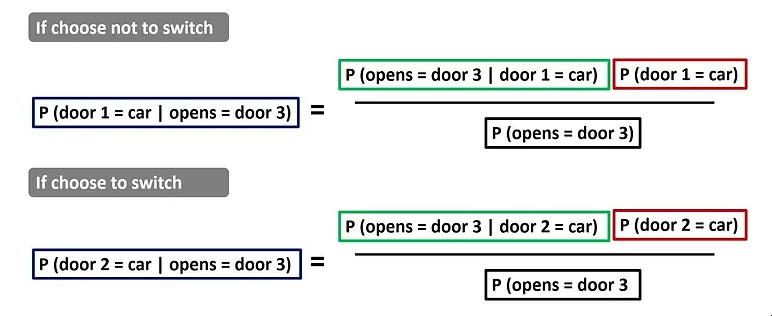
为了解决这个问题,让我们应用贝叶斯定理公式并比较
P(门1 = 车| 打开=门3)
P(门2 = 车| 打开=门3)
贝叶斯定理在蒙蒂霍尔问题中的应用
先验概率 P(A)
让我们从最简单的计算概率开始,先验概率。这是指在游戏开始时,在门 1 打开之前,汽车在门 2 和门 3 后面的初始预期概率。
假设汽车是随机分配的,每扇门都有平等的机会让汽车落后。因此,P(门1 = 汽车)和 P(门 2 = 车)的概率相等为 1/3。
可能性 P(B|A)
接下来,我们将计算主持人为各自的假设打开门 3 的可能性。
第1个假设,如果汽车在门 1 后面,主持人可以打开门 2 或门 3 以露出一只山羊。因此:
P(打开 = 门 3 | 门 1 = 汽车) = 1/2
另一方面,如果汽车在门 2 后面,主持人别无选择,只能打开门 3,因为它是唯一的一扇门后有山羊的门。因此,对于第二个假设,
P(打开 = 门 3 | 门 2 = 汽车) = 1
联合概率 P(B|A) X P(A)
在已知可能性和先验概率值的情况下,我们可以计算出两个假设的公式的分子值。
P(打开 = 门 3 | 门 1 = 汽车) X P(门 1 = 汽车) = 1/2 X 1/3 = 1/6
P(打开 = 门 3 | 门 2 = 汽车) X P(门 1 = 汽车) = 1 X 1/3 = 1/3
观察到的证据概率 P(B)
我们可以通过简单地将联合概率相加来得出观察到的证据的概率。此值表示主持人在参赛者选择门 3 的情况下选择打开门 1 的概率。
P(打开 = 门 3) = 1/6 + 1/3 = 1/2
后验概率 P(A|B)
最后,我们可以通过将上述所有派生值输入公式来求解后验概率。
P(门 1 = 汽车 | 打开 = 门 3) = (1/6) / (1/2) = 1/3
P(门 2 = 汽车 | 打开 = 门 3) = (1/3) / (1/2) = 2/3
后验概率值告诉我们,主持人在门 1 后面有山羊,坚持选择门 3,那么赢得汽车的几率是 1/3。相反,如果我们选择接受切换到门 2 的提议,我们的机会就会翻倍到 2/3。
因此,贝叶斯方法支持Marilyn vos Savant的建议,即如果可以选择,请始终进行切换。
像频率主义者一样思考
与贝叶斯方法相反,顾名思义,频率主义者根据采样频率来确定概率。例如,如果我们想知道在抛硬币中获得“正面”的概率,我们可以掷硬币进行x次试验,并根据“正面”发生的频率分布确定概率。
正如伯努利大数定律所声称的那样,事件发生的长期频率将收敛于其理论概率。因此,为了解决Monty Hall问题,我们可能会在大量的试验中运行游戏节目谜题的模拟,并比较坚持我们最初选择的决定和改变选择的决定之间的赢得汽车的频率。
对于这个项目,我使用python编程语言执行了蒙特卡罗模拟。蒙蒂霍尔游戏被模拟了相当多的重复,并记录了各自策略的获胜几率。模拟唯一需要的包是随机包。首先,我创建了三个空列表来存储每个示例模拟的结果。
初始化空的数组存放模拟过程中的数
chance_of_winning_ifswitch_list = []
#放弃最初选择,改选另外的门
chance_of_winning_ifdonotswitch_list = []
#坚持最初选择的门
percentage_diff_list = []
相差的百分比
接下来,使用“for-loops”设置模拟。
在每个模拟循环中,汽车和山羊的位置被随机分配,并选择随机门作为参赛者的初始选择。鉴于游戏主持人总是会用山羊打开另一扇门,只有当最初选择的门碰巧后面有汽车奖品时,切换的决定才会适得其反。
换句话说,如果选择不切换选择,获胜的概率相当于当初选择带车门的概率。因此,包含一个“if-else”条件语句来检查最初选择的门是否有汽车。
如果所选门后面没有汽车,我们分配一个值 1 来表示选择切换选项时的获胜事件。如果所选门后面有汽车,我们分配一个值 0 来表示选择不切换选择时的获胜事件。
为了确定每种策略的获胜频率,获胜的几率是根据Monty Hall游戏的1,000个模拟回合的样本计算的。
此抽样重复 10,000 次,以确定每种策略的获胜百分比分布。设置随机种子值以确保结果的可重复性。
# Repeat 10000 trials with 1000 samples per trial
for i in range(10000):
results_list = []
for i in range(1000):
door_list = ["car", "goat", "goat"]
random.shuffle(door_list)
chosen_door_number = random.sample(range(3), 1)
chosen_door = door_list[chosen_door_number[0]]
if chosen_door != "car":
results_list.append(1)
else:
results_list.append(0)
# Compute winning percentage if choose to switch
chance_of_winning_ifswitch = sum(results_list)/len(results_list)*100
# Compute winning percentage if choose not to switch
chance_of_winning_ifdonotswitch = 100 - chance_of_winning_ifswitch
# Compute difference in winning percentage between the two strategies
percentage_diff = chance_of_winning_ifswitch - chance_of_winning_ifdonotswitch
# Append the results to respective lists
chance_of_winning_ifswitch_list.append(chance_of_winning_ifswitch)
chance_of_winning_ifdonotswitch_list.append(chance_of_winning_ifdonotswitch)
percentage_diff_list.append(percentage_diff)
下图说明了基于我们的模拟结果的两种策略的获胜赔率分布。蓝色直方图表示策略切换的分布,而黄色直方图表示策略坚持初始选择的分布。
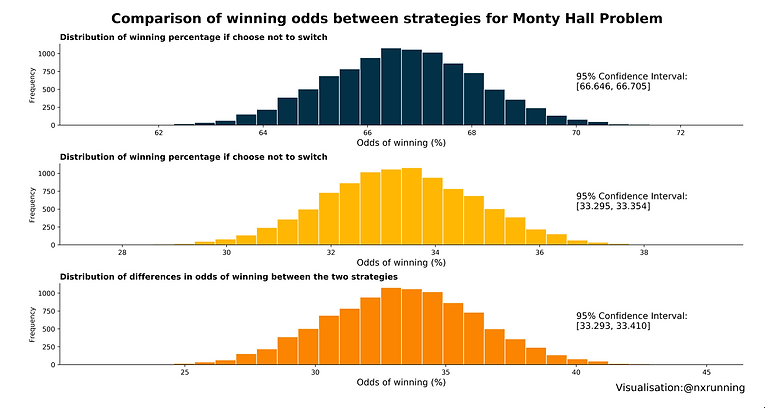
根据中心极限定理,当样本量较大时,样本均值的分布将近似于高斯分布或正态分布。正如我们从大量模拟试验中预期的那样,我们观察到一条钟形曲线,该曲线表征了正态分布。
两个直方图的 x 轴清楚地表明了两种策略之间的获胜几率差异。
如果你选择切换,62-72%的机会开着车回家,而如果你选择不切换,则有28-38%的机会。
为两种策略计算的 95% 置信区间进一步支持了这一点。在 95,10 次试验抽样获胜赔率的 000% 内,如果您切换,获胜的频率在 66.646% 和 66.705% 之间,而坚持相同的门选择将在 33.295% 和 33.354% 之间。
由于 95% 置信区间不重叠,我们可以推断两种策略之间的胜率存在统计上的显著差异。
事实上,如第三个直方图橙色所示,我们有 95% 的信心选择切换会使我们的获胜几率增加 33.293 至 33.410%。因此,频率主义的方法也支持玛丽莲·沃斯·萨凡特的建议,即如果可以选择,请始终进行切换。
结论
这篇博文展示了使用贝叶斯和频率主义方法来解决蒙蒂霍尔问题。通过上面的例子,我们可以看到推导概率值的不同方法。
虽然这两种方法不同,但在蒙蒂霍尔问题的背景下,推导出的概率彼此相似。结果清楚地表明,无论你是赞同贝叶斯范式还是频率范式,改变你的选择总是一个更明智的选择,以增加赢得汽车的机会。
模拟、分析和可视化都是使用 Python 进行的。
# Import required packages
import random
import numpy as np
import scipy.stats
import matplotlib.pyplot as plt
import pandas as pd
####----Create Monty Hall Game Simulation----####
# Create empty lists to store simulation results output
chance_of_winning_ifswitch_list = []
chance_of_winning_ifdonotswitch_list = []
percentage_diff_list = []
# Set a seed value for reproducibility
random.seed(1234)
# Create simulation using for-loops
# Repeat 10000 trials with 1000 samples per trial
for i in range(10000):
results_list = []
for i in range(1000):
door_list = ["car", "goat", "goat"]
random.shuffle(door_list)
chosen_door_number = random.sample(range(3), 1)
chosen_door = door_list[chosen_door_number[0]]
if chosen_door != "car":
results_list.append(1)
else:
results_list.append(0)
chance_of_winning_ifswitch = sum(results_list)/len(results_list)*100 # Compute winning percentage if choose to switch
chance_of_winning_ifdonotswitch = 100 - chance_of_winning_ifswitch # Compute winning percentage if choose not to switch
percentage_diff = chance_of_winning_ifswitch - chance_of_winning_ifdonotswitch # Compute difference in winning percentage between the two strategies
# Append the results to respective lists
chance_of_winning_ifswitch_list.append(chance_of_winning_ifswitch)
chance_of_winning_ifdonotswitch_list.append(chance_of_winning_ifdonotswitch)
percentage_diff_list.append(percentage_diff)
####----Analysis of the simulation results----####
# Create a function to calculate 95% confidence intervals
def mean_confidence_interval(data, confidence=0.95):
a = 1.0 * np.array(data)
n = len(a)
m, se = np.mean(a), scipy.stats.sem(a)
h = se * scipy.stats.t.ppf((1 + confidence) / 2., n-1)
return m, m-h, m+h
# Compute 95% confidence intervals of chance of winning if choose to switch
mean_confidence_interval(chance_of_winning_ifswitch_list)
# Compute 95% confidence intervals of chance of winning if choose not to switch
mean_confidence_interval(chance_of_winning_ifdonotswitch_list)
# Compute 95% confidence intervals of difference in chances of winning between the two strategies
mean_confidence_interval(percentage_diff_list)
####----Simple visualisation of the simulation results----####
fig = plt.figure(figsize = (15,8))
ax1, ax2, ax3 = fig.subplots(3, 1)
# Title and caption of plot
fig.suptitle("Comparison of winning odds between strategies", fontsize = 20, fontweight = "bold")
fig.text(.99, .010, "Visualisation:@nxrunning", ha='right', fontsize = 15)
# Subplot number 1
ax1.set_title("Distribution of winning percentage if choose not to switch", loc = "left", fontweight = "bold")
ax1.hist(chance_of_winning_ifswitch_list, alpha = 1, color = "#023047", edgecolor = "white", bins = (30))
ax1.set_ylabel("Frequency")
ax1.set_xlabel("Odds of winning (%)", fontsize = 13)
ax1.annotate("95% Confidence Interval:\n[66.646, 66.705]", xy = (70, 500), fontsize = 13)
# Subplot number 2
ax2.set_title("Distribution of winning percentage if choose not to switch", loc = "left", fontweight = "bold")
ax2.hist(chance_of_winning_ifdonotswitch_list, alpha = 1, color = "#ffb703", edgecolor = "white", bins = (30))
ax2.set_xlabel("Odds of winning (%)", fontsize = 13)
ax2.set_ylabel("Frequency")
ax2.annotate("95% Confidence Interval:\n[33.295, 33.354]", xy = (36.7, 500), fontsize = 13)
# Subplot number 3
ax3.set_title("Distribution of differences in odds of winning between the two strategies", loc = "left", fontweight = "bold")
ax3.hist(percentage_diff_list, alpha = 1, color = "#fb8500", edgecolor = "white", bins = (30))
ax3.set_ylabel("Frequency")
ax3.set_xlabel("Odds of winning (%)", fontsize = 13)
ax3.annotate("95% Confidence Interval:\n[33.293, 33.410]", xy = (40, 500), fontsize = 13)
fig.tight_layout()
# Removing top and right borders
ax1.spines['top'].set_visible(False)
ax1.spines['right'].set_visible(False)
ax2.spines['top'].set_visible(False)
ax2.spines['right'].set_visible(False)
ax3.spines['top'].set_visible(False)
ax3.spines['right'].set_visible(False)
# Adjust space between title and subplots
plt.subplots_adjust(top=0.90)
# Save plot
fig.savefig('Montyhallproblemsimulation.png', dpi=500)
完整的代码可以在这里找到。
本文由 mdnice 多平台发布