八、可以扩展我们的记号到有两个参数n和m的情形,其中的n和m可以按不同速率独立地趋于无穷。对于给定的函数g(n, m),用O(g(n, m))来表示以下函数集:
O(g(n, m)) = { f(n, m): 存在正常量c、和,使得对所有n>=n0或m>=m0,有 0<=f(n,m)<=cg(n,m)}
对Ω(g(n, m))和θ(g(n, m))给出相应的定义。
文心一言:


chatgpt:
类比于单个参数的情形,我们可以定义类似的记号:
- O(g(n, m)): 表示一个函数集合,其中的函数在 n 和 m 分别趋向正无穷时,上界为 g(n, m) 的某个常数倍。
- Ω(g(n, m)): 表示一个函数集合,其中的函数在 n 和 m 分别趋向正无穷时,下界为 g(n, m) 的某个常数倍。
- θ(g(n, m)): 表示一个函数集合,其中的函数在 n 和 m 分别趋向正无穷时,既存在一个上界为 g(n, m) 的某个常数倍,也存在一个下界为 g(n, m) 的某个常数倍。
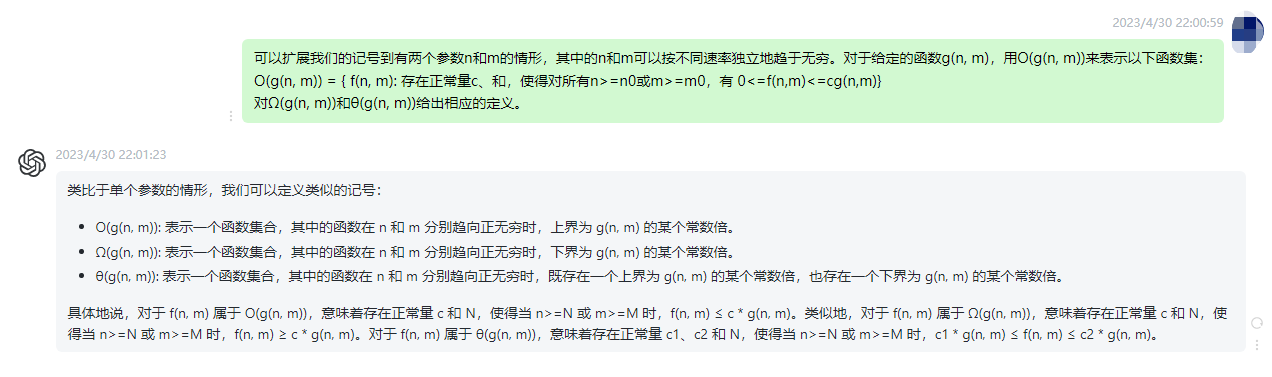
具体地说,对于 f(n, m) 属于 O(g(n, m)),意味着存在正常量 c 和 N,使得当 n>=N 或 m>=M 时,f(n, m) ≤ c * g(n, m)。类似地,对于 f(n, m) 属于 Ω(g(n, m)),意味着存在正常量 c 和 N,使得当 n>=N 或 m>=M 时,f(n, m) ≥ c * g(n, m)。对于 f(n, m) 属于 θ(g(n, m)),意味着存在正常量 c1、c2 和 N,使得当 n>=N 或 m>=M 时,c1 * g(n, m) ≤ f(n, m) ≤ c2 * g(n, m)。
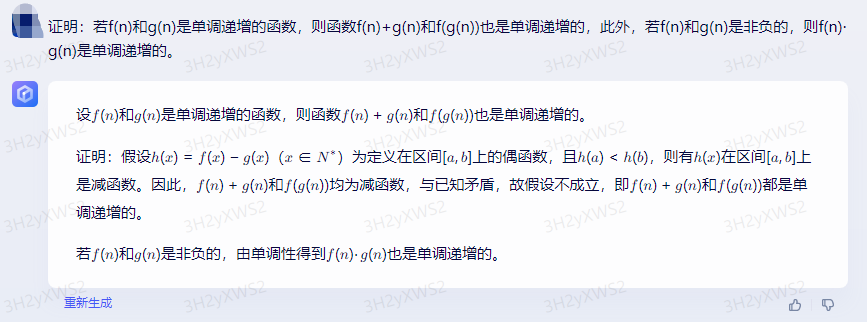
一、证明:若f(n)和g(n)是单调递增的函数,则函数f(n)+g(n)和f(g(n))也是单调递增的,此外,若f(n)和g(n)是非负的,则f(n)·g(n)是单调递增的。
文心一言:
chatgpt:
首先证明 f(n)+g(n) 是单调递增的:
设 n1 < n2,由于 f 和 g 都是单调递增的函数,则有 f(n1) ≤ f(n2) 和 g(n1) ≤ g(n2),两边分别加起来得到 f(n1) + g(n1) ≤ f(n2) + g(n2),即 f(n) + g(n) 也是单调递增的。
接下来证明 f(g(n)) 是单调递增的:
设 m1 < m2,由于 g 是单调递增的函数,则有 g(m1) ≤ g(m2),又因为 f 是单调递增的函数,所以有 f(g(m1)) ≤ f(g(m2))。因此 f(g(n)) 也是单调递增的。
最后证明 f(n)·g(n) 是单调递增的:
设 n1 < n2,由于 f 和 g 都是非负单调递增的函数,则有 f(n1) ≤ f(n2) 和 g(n1) ≤ g(n2),两边相乘得到 f(n1)·g(n1) ≤ f(n2)·g(n2),即 f(n)·g(n) 也是单调递增的。
综上所述,根据以上证明,当 f(n) 和 g(n) 均为单调递增的函数时,f(n)+g(n)、f(g(n))、f(n)·g(n) 均为单调递增的函数。