目录
前言
文献阅读
背景
对现有技术的分析
主要思路和贡献
相关性分析和归一化处理
相关性分析
归一化处理
TCN
基于 TCN-LSTM 的 PM 浓度预测模型
敏感性分析
论文思路
求半方差
训练模型 -1
训练模型-2
总结
前言
This week I studied an article that constructed a TCN-LSTM model to predict atmospheric PM concentrations. Among them, TCN is a simple CNN model, which is mainly used to solve time series problems, and its role is to ensure the stability of data feature extraction. PM concentration prediction is a time series prediction problem with nonlinear characteristics, and LSTM is used to deal with it because the LSTM model, as a variant of classical RNNs, has nonlinear entity fitting ability, making it suitable for dealing with sequential modeling problems. Finally, the study employs the sensitivity analysis method Sobol, a global sensitivity analysis method based on ANOVA that can be used to analyze the degree to which multiple parameters affect the output of the model. In addition, there have been new developments in the application of kriging interpolation.
本周我学习了一篇文章,该研究构建了TCN-LSTM模型来预测大气PM浓度。其中TCN是一种简单的CNN模型,主要用于解决时间序列问题,作用是保证数据特征提取的稳定。PM浓度预测是一个具有非线性特征的时间序列预测问题,采用LSTM来处理是因为LSTM 模型作为经典 RNN 的变体,具有非线性实体拟合能力,使其适用于处理顺序建模问题。最后一点是该研究采用了敏感性分析方法Sobol,这是一种基于方差分解的全局敏感性分析方法,可用于分析多个参数对模型输出结果的影响程度。除此之外,在克里金插值法的应用上,有了新的进展。
文献阅读
--Ying Ren, Siyuan Wang, Bisheng Xia,
Deep learning coupled model based on TCN-LSTM for particulate matter concentration prediction,
Atmospheric Pollution Research,
Volume 14, Issue 4,
2023,
101703,
ISSN 1309-1042,
https://doi.org/10.1016/j.apr.2023.101703.
背景
大气颗粒物(PM)是雾霾天气发生的主要因素之一,在全球范围内越来越受到关注。大气中的PM主要包括PM2.5(空气动力学直径为 <2.5 μm)的 PM 和 PM10(空气动力学直径为 <10 μm) 的 PM),主要包括水溶性离子、PM 和有机物。PM的来源可分为两大类:天然来源和人工来源。自然来源主要包括岩石和土壤的风化、森林火灾、火山喷发和海盐颗粒,而人工来源主要包括车辆尾气排放、工业排放、建筑工地粉尘和垃圾焚烧。大气PM浓度的增加会导致人们呼吸道疾病和心血管疾病增加的可能性,也推动了全球气候的变化。PM的准确高效预测在雾霾天气管理和人类可持续发展方面具有不可忽视的作用。

对现有技术的分析
目前用于大气PM预测的主要方法包括基于物理的机理模型和数据驱动的统计模型。机制模型主要包括社区多尺度空气质量模型,操作街道污染模型和嵌套空气质量预测模型。区域大气动力学天气研究与预报模型结合化学广泛用于模拟PM的形成和分散。然而,这种机械模型的使用是基于特定条件的假设,现实的表示往往是可变的。默认参数设置限制了机理模型的性能,导致精度低于特定地点的经验空气质量预测模型。
传统的统计模型不使用复杂的物理参数,而是根据历史数据预测空气污染物浓度。例如,多元线性回归,自回归积分移动平均线以及地理和时间加权回归模型将变量之间的关系视为线性关系,与大多数现实世界的情况相反。为了解决这个问题,许多研究人员使用非线性机器学习技术(例如人工神经网络)预测了大气污染物的浓度,随机森林(RF)和支持向量回归 (SVR)方法。然而,随着数据量和模型训练时间的增加,此类模型方法的特征提取能力和学习能力下降,从而导致模型预测精度下降。更重要的是,此类模型没有存储单元,无法解释污染物数据的时间特征。一些学者将机器学习模型与其他模型结合使用来研究 PM,这些组合模型的思想为大气PM研究提供了新的思路。
近年来,随着深度学习的兴起,许多研究已将此类技术应用于环境领域,其中使用最广泛的深度学习方法是递归神经网络 (RNN) 模型和卷积神经网络 (CNN) 模型。由于其独特的自环结构,适用于处理顺序数据,RNN 已被应用于预测 PM 浓度。然而,RNN模型存在长期依赖性和梯度消失问题,这些问题可以通过派生的长短期记忆(LSTM)网络模型很好地解决。LSTM方法在环境预测中的应用通常与CNN模型相结合,可以并行处理信息,具有强大的特征提取能力。因此,CNN-LSTM 模型适用于空气质量指数的预测和其他大气物质。但是,CNN结构复杂,当输入和输出信息的维度不同时,可能会导致信息丢失。为了解决这个问题,有学者提出了时间卷积网络(TCN)。TCN既具有CNN的并行特性,又具有RNN的记忆功能。TCN可以对复杂的序列数据进行快速特征提取,并确保输入和输出信息的维度相同。其优异的特征提取能力在恶劣天气预报、短期交通预测、多变量时间序列预测和计算机视觉等领域得到广泛利用,并且所有此类应用都报告了令人满意的结果。
深度学习模型的性能受输入的影响,识别此类模型的关键输入变量有利于提高预测效率和降低建模成本。更重要的是,大气污染物的形成很复杂,深度学习模型无法识别污染物的主导因素。敏感性分析方法在环境领域用于识别影响模型输出、减少模型输入和避免参数冗余的关键变量,同时分析模型输入变量与目标输出之间的不确定关系以提高模型适用性。敏感性分析与深度学习模型相结合不仅可以帮助模型消除不必要的输入,还可以解释模型的目标输出,以揭示不同影响因素对城市空气污染物的影响。
主要思路和贡献
于上述分析,本研究结合TCN和LSTM模型,设计了一种新的颗粒浓度预测模型TCN-LSTM模型。本文的主要著作有:
(1)构建了TCN-LSTM混合模型,选取低成本、现成的气象因子和污染物浓度数据进行建模。TCN模型从PM的影响因素中提取特征。LSTM模型学习提取的特征来预测西安市大气中的PM浓度。将预测结果与经典深度学习模型(CNN-LSTM、LSTM、TCN)和机器学习(SVR和RF)进行比较,并通过RMSE、MSE、MAE和R进行对比和验证。2指标,结果表明TCN-LSTM表现更好。此外,TCN-LSTM模型还用于预测北京、上海、成都和深圳的PM浓度,该模型仍然表现良好。在交叉验证的实验中,TCN-LSTM模型仍然表现稳定;
(2)采用敏感性分析法研究各影响因素对西安市疫情前(2015—2019年)和疫情后(2020—2022年)PM浓度的影响,并与2015—2022年全期敏感性分析结果进行比较;
(3)使用灵敏度分析方法来评估模型的输入变量对目标输出的贡献程度。利用对模型输出贡献较大的参数,构建PM浓度快速预测模型,降低建模成本。
相关性分析和归一化处理
相关性分析

其中PM之间的相关性最高PM2.5和PM10,皮尔逊系数为0.86。两位PM2.5和PM10是大气中的PM并且相似。因此,使用一个模型进行PM研究就足够了。
归一化处理

数据,包括风速(WS),风向(WD),相对湿度(RH),降水(PR),压力(P)温度(T),露点(DP)和太阳辐照度(SI)。在这项研究中,PM指标用作输出变量,其他指标用作输入变量。使用以下归一化公式对每个变量(风向除外,风向数据转换为独热代码)进行归一化,消除了可归因于维度差异的误差
TCN

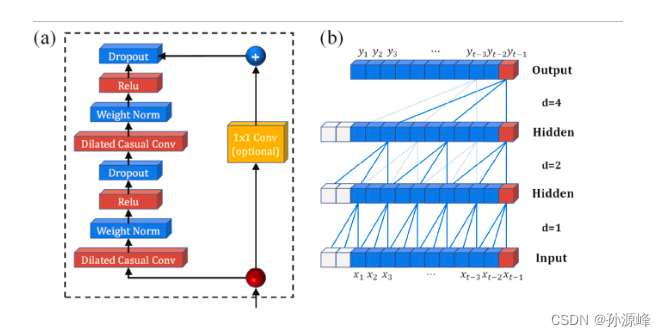
一旦扩张的因果卷积完成,使用WeightNorm对每层的权重进行归一化,使用激活函数Relu进行非线性计算,Dropout操作控制丢弃神经元的概率以使某些神经元失活以避免过度拟合。如果残差块的输入和输出向量形状不同,则使用一维卷积改变输入信息的维数,驱动网络产生与输入相同维数的输出。
基于 TCN-LSTM 的 PM 浓度预测模型

TCN独特的一维因果卷积结构保证了数据的时间序列特征,残差连接单元加速了网络的收敛速度,扩展卷积保证了所有数据特征的提取。LSTM 模型作为经典 RNN 的变体,具有非线性实体拟合能力,使其适用于处理顺序建模问题。PM浓度预测是一个具有非线性特征的时间序列预测问题。影响PM浓度的因素有颗粒物本身浓度的增加/减少、大气中其他污染物的含量以及气象因素。本研究将TCN模型与LSTM模型相结合,构建了考虑多因素形成和颗粒非线性特征的大气PM浓度预测TCN-LSTM模型。TCN-LSTM模型的架构如图所示,预测PM浓度的主要过程如下所述。
(1)获取的气象和污染物数据经过处理,按照特定比例分为测试集和训练集。训练集用于调整模型的超参数。训练集作为TCN模型的输入,TCN模型对输入信息进行特征提取。TCN模型提取数据后,数据的杂质将大大减少,特征暴露更加明显,有利于LSTM模型的学习。
(2)TCN模型提取的特征输入到LSTM模型,LSTM模型通过遗忘门、输入门和输出门控制网络的输出,记住需要长期记忆的关键信息,忘记不重要的信息,使模型能够处理长期串行数据,准确预测下一刻PM的浓度。
(3)将训练集的预测目标与预测结果进行比较,计算训练集的损失,确定损失最小化,并确定模型参数,以确保模型得到最佳调优。测试集用作模型的输入,以验证损失是否最小化并完成预测任务。
本研究中使用的程序是用Python语言编写的,基于TensorFlow 2.0框架。使用亚当优化器对整个模型进行优化,将均方误差(MSE)函数用作模型的损失函数(Nhu等人,2020),并通过训练不断调整每个模型参数。整个过程可以表示如下:

其中功能1表示TCN层学习的结果,TCN(⋅)表示TCN层和TCN层相关的操作,特征2表示 LSTM 层学习的结果,LSTM(⋅) 表示与 LSTM 层和 LSTM 层相关的运算,a(xt) 表示归一化后的相关序列信息,F(xt) 表示模型的输出,Linear(⋅) 表示全连接层的线性映射。
以1年2015月8日至2021年9月2021日的数据作为训练集来训练每个模型条目,将9年2022月<>日至<>年<>月<>日的数据作为测试集,使用训练好的模型测试模型。均方根误差 (RMSE)、平均绝对误差 (MAE)、MSE 和相关系数 (R2)被选为评估模型预测能力的指标。
敏感性分析

论文思路
求半方差
假设已有实验数据,包括一组空间位置坐标和对应的半方差值(半方差表示空间点间的相似度),那么可以用以下Python代码计算克里金插值的半方差:
这段代码使用了numpy和scipy库,其中get_semivariance函数用于计算输入数据的半方差函数,krige_semivariance函数则是克里金插值法的核心实现。该函数接受三个参数:输入数据、空间坐标、最大距离和分bin数目。输出为一个长度为num_bins的半方差数组。
import numpy as np
from scipy.spatial.distance import pdist, squareform
# 根据输入数据计算半方差函数
def get_semivariance(data, max_dist, num_bins):
dist_matrix = squareform(pdist(data[:, :2]))
bins = np.linspace(0, max_dist, num_bins)
semivariance = np.zeros(num_bins)
for i in range(num_bins):
indices = np.where((dist_matrix >= bins[i]) & (dist_matrix < bins[i+1]))
if len(indices[0]) > 0:
semivariance[i] = 0.5 * np.mean((data[indices[0], 2] - data[indices[1], 2])**2)
return semivariance
# 克里金插值法计算半方差
def krige_semivariance(data, coords, max_dist, num_bins):
semivariance = get_semivariance(data, max_dist, num_bins)
X = coords[:, 0]
Y = coords[:, 1]
# 计算距离矩阵
dist_matrix = squareform(pdist(coords))
# 初始化变量
n = len(coords)
A = np.ones((n+1, n+1))
A[:n, :n] = -0.5 * dist_matrix**2 * semivariance[1]
A[n, :] = 1
A[:, n] = 1
A[n, n] = 0
b = np.zeros(n+1)
b[-1] = 1
# 求解线性方程组
weights = np.linalg.solve(A, b)
# 计算半方差函数值
h = np.zeros(num_bins)
for i in range(num_bins):
r = bins[i] * np.ones((n, n)) + dist_matrix
h[i] = np.sum(weights[:-1] * semivariance[np.digitize(r.flat, bins)])
return h
训练模型 -1
将克里金插值法的半方差作为输入数据,输出数据则可以根据具体问题而定。假设我们的问题是预测某个位置的空气质量指数(AQI),那么输出数据就是该位置对应的 AQI 值。
这里使用 Keras 的 Sequential API 构建了一个简单的 LSTM 模型。其中 units 参数表示 LSTM 层的神经元数量,input_shape 参数表示输入数据的形状,即 (batch_size, time_steps, features)。Dense 层用于将 LSTM 层的输出连接到一个全连接层以产生最终的输出。模型使用均方误差(MSE)作为损失函数,Adam 优化器进行训练。
在完成模型训练后,可以将其保存到文件中以备后续使用。
下面是一个简单的 LSTM 模型代码:
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dense
# 加载训练集和测试集
X_train = np.load('X_train.npy') # 训练集输入数据
y_train = np.load('y_train.npy') # 训练集输出数据
X_test = np.load('X_test.npy') # 测试集输入数据
y_test = np.load('y_test.npy') # 测试集输出数据
# 定义 LSTM 模型
model = Sequential()
model.add(LSTM(units=64, input_shape=(X_train.shape[1], X_train.shape[2])))
model.add(Dense(units=1))
model.compile(optimizer='adam', loss='mse')
# 训练模型
model.fit(X_train, y_train, epochs=50, batch_size=32, validation_data=(X_test, y_test))
# 保存模型
model.save('lstm_model.h5')
训练模型-2
如果输入函数除了克里金插值法的半方差之外,还有其他特征,比如位置的湿度,那么可以将这些特征一起作为 LSTM 模型的输入。假设数据集包含以下特征:
- 半方差
- 湿度
- 经度
- 纬度
那么可以按照以下方式准备训练和测试数据:
import numpy as np
# 加载数据集
data = np.load('data.npy') # 包含全部特征的数据集,形状为 (num_samples, num_features)
# 提取半方差、湿度、经度和纬度特征
semivariance = data[:, 0]
humidity = data[:, 1]
longitude = data[:, 2]
latitude = data[:, 3]
# 将特征组合成训练和测试数据
X_train = np.zeros((num_train_samples, time_steps, num_features))
y_train = np.zeros((num_train_samples, 1))
X_test = np.zeros((num_test_samples, time_steps, num_features))
y_test = np.zeros((num_test_samples, 1))
for i in range(num_train_samples):
X_train[i, :, 0] = krige_semivariance(train_data[i], coords, max_dist, num_bins)
X_train[i, :, 1] = train_data[i][:, 2] # 湿度特征
X_train[i, :, 2] = train_data[i][:, 0] # 经度特征
X_train[i, :, 3] = train_data[i][:, 1] # 纬度特征
y_train[i, 0] = train_data[i][0, 3] # AQI 输出值
for i in range(num_test_samples):
X_test[i, :, 0] = krige_semivariance(test_data[i], coords, max_dist, num_bins)
X_test[i, :, 1] = test_data[i][:, 2]
X_test[i, :, 2] = test_data[i][:, 0]
X_test[i, :, 3] = test_data[i][:, 1]
y_test[i, 0] = test_data[i][0, 3]
在这个例子中,我们将半方差、湿度、经度和纬度四个特征组合成了输入数据。X_train 和 X_test 的形状分别为 (num_train_samples, time_steps, num_features) 和 (num_test_samples, time_steps, num_features),其中 time_steps 表示时间步长,num_features 表示每个时间步长的特征数。y_train 和 y_test 则表示对应的输出值。
有了完整的输入数据后,就可以按照之前的代码编写 LSTM 模型了,只需要增加一个 input_shape 参数即可:
model = Sequential()
model.add(LSTM(units=64, input_shape=(time_steps, num_features)))
model.add(Dense(units=1))
model.compile(optimizer='adam', loss='mse')
model.fit(X_train, y_train, epochs=50, batch_size=32, validation_data=(X_test, y_test))
这里的 input_shape 参数为 (time_steps, num_features),对应于输入数据的形状。如果希望在 LSTM 层之前添加其他层(如卷积层或池化层),需要根据具体情况调整 input_shape 参数。
总结
放假期间事情比较多,学的东西一知半解。下周我将对于论文的整体思路展开分析,希望能尽快完成整篇论文。