C++语法（21）---- 模拟map和set_哈里沃克的博客-CSDN博客https://blog.csdn.net/m0_63488627/article/details/130354019?spm=1001.2014.3001.5501

目录

1.哈希表的介绍

1.stl中的哈希表使用

2.比较

3.哈希的原理

4.哈希映射的方法

1.直接定址法

2.除留余数法

5.解决哈希冲突

1.闭散列

2.开散列(哈希桶)

---

1.哈希表的介绍

1.stl中的哈希表使用

unordered_map(K,V)

unordered_set(K)

hash<KEY>其实是一个仿函数，是因为数据要和位置映射，那必然要取余，string等类无法使用取余，那么需要我们自己写一个进行判断。

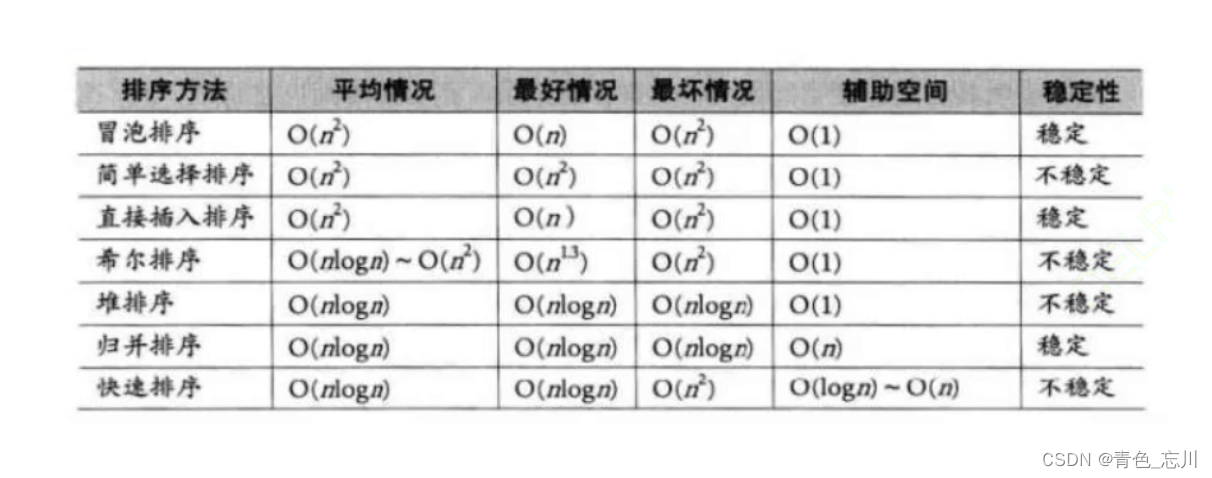
2.比较

其上层的使用与map以及set及其的相近。但是又有什么不同呢

1.大量随机数据插入，map和set性能快

2.查找数据，哈希表级制性能，时间复杂度为O(1)

3.大量随机数据删除，也是map和set性能快

3.哈希的原理

就是将数据和存储位置做一个映射，这个映射就是哈希映射。所以使用哈希表的好处就是找到自己想要的数据时间复杂度很低

4.哈希映射的方法

1.直接定址法

取关键字的某个线性函数为散列地址：Hash（Key）= A*Key + B -- 某个值都要唯一的位置
优点：简单、均匀
缺点：需要事先知道关键字的分布情况，如果数据比较分散开辟空间会很浪费
使用场景：适合查找比较小且连续的情况

2.除留余数法

设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，
按照哈希函数：Hash(key) = key% p(p<=m),将关键码转换成哈希地址  --  几个值都可能在同一个位置

优点：空间适合
缺点：这种情况，会存在可能多个值取余后得到相同的映射地址(哈希冲突)

使用场景：适合分散的场景

5.解决哈希冲突

1.闭散列

实现原理：冲突位置，那么往后判断是否是否为空

缺点：查找效率变低，互相冲突导致插入逻辑复杂

1.线性探测(一个萝卜一个坑，坑被占了线性往后找下一个空的)  ---  start+i

2.二次探测，是以平方为步调向后判断的  ---  start+i^2

线性探测实现：

表内元素的状态

冲突主要是因为一个数已经存在于表中，那么才需要往后判断是否为空，所以已经知道需要两个状态：存在和空。不过如果我们要往后搜索，如果只有两个结果，那么在连续冲突的数中删除，那么数据就中断了，那么实现就会出现错误，那么此时还需要一个状态表示：删除。

enum State
{
	EMPTY,
	EXIST,
	DELETE,
};

元素属性定义

此外为了保持和map的一致性，我们的节点元素也要使用pair与之对应，并且伴随节点的状态，节点先处理为empty，说明数组中的状态为空

template<class K, class V>
struct HashData
{
	pair<K, V> _kv;
	State _state = EMPTY;;
};

表的框架

当然，对于一个模板，并不知道比较大小是通过什么方式比较的，所以我们还得添加上仿函数进行比较。

template<class K>
struct HashFunc
{
	size_t operator()(const K& k)
	{
		return (size_t)k;
	}
};

//特化了一个string的仿函数，它的大小比较按照我想要的方式实现
template<>
struct HashFunc<string>
{
	size_t operator()(const string& k)
	{
		size_t hash = 0;
		for (auto& ch : k)
		{
			hash += ch;
		}
		return hash;
	}
};

template<class K, class V, class Hash = HashFunc<K>>
class HashTable
{
	typedef HashData<K, V> Data;
public:
	HashTable()
	{
		_tables.resize(10);
	}
private:
	vector<Data> _tables;  //存储数据的空间
	size_t _n = 0;  //进去的数有多少
};

insert

关于capacity和size问题，首先我们插入的位置一定的在size内，因为如果是判断capacity，那么值的映射可能会在capacity和size之间，但是size只有那么大，所以找不到映射后的位置也有可能，所以判断靠判断和size的大小的。不过我们可以设计成size和capacity一样大，这样就不会出现这种尴尬。capacity和size一致，我们使用resize()函数就能解决。

实现逻辑就是：当判断映射位置为存在，那么我们就需要往后找，不过不能超过整体范围，所以我们需要对hashi进行取余处理。随后找到位置则插入，状态设置为EXIST，将_n加一。

Hash hf;  //仿函数
size_t hashi = hf(kv.first) % _tables.size();
//线性探测
while (_tables[hashi]._state == EXIST)
{
	hashi++;
	hashi %= _tables.size();
}

_tables[hashi]._kv = kv;
_n++;
_tables[hashi]._state = EXIST;

return true;

出现了有些问题：

问题：表的数据存储满了，那就有扩容问题  ---  此外，暂且不说存储满了，如果数据很多都被覆盖了，那么此时再想插入是不是也就意味着非常容易冲突呢？此时插入成本就很高了

结论：所以我们不能让它满，我们需要添加一个负载因子，使得我们在表中出现百分之几十后说明我们需要扩容。负载因子越小，说明固定空间中的数据越少，那么使得冲突的几率就小。不过太小浪费空间，太大浪费时间，所以设计的负载因子一般为0.7。

实现：

1.此时我们要注意，不能直接跟size比较是否小于0.7，因为int类型不能这样比较，所以我们要对_n*10随后比较是否小于7。

2.扩容不能直接把vector变大就好，因为里面的数据可能会对不上之后扩容的映射地址。所以我们新建一个表，再将原来的值依次insert进新表中，在把两表互换，新表出insert函数就被自动析构了。

3.此外map设置就不能出现两个相同的值，所以我们还会实现一个find函数，通过find函数找是否已经存在，如果存在则插入失败。

bool Insert(const pair<K, V>& kv)
{
	if (Find(kv.first) != nullptr)
		return false;
	if (_n * 10 / _tables.size() >= 7)
	{
		HashTable<K, V, Hash> tmp;
		tmp._tables.resize(2 * _tables.size());
		for (auto& e : _tables)
		{
			if (e._state == EXIST)
			{
                //复用了自己写的insert函数
				tmp.Insert(e._kv);
			}
		}
		_tables.swap(tmp._tables);
	}

	Hash hf;
	size_t hashi = hf(kv.first) % _tables.size();

	//线性探测
	while (_tables[hashi]._state == EXIST)
	{
		hashi++;
		hashi %= _tables.size();
	}

	_tables[hashi]._kv = kv;
	_n++;
	_tables[hashi]._state = EXIST;

	return true;
}

erase

先find(后面实现)想要删除的值，随后把插入的值的状态设置为DELETE即可，_n减一

bool Ereas(const K& k)
{
	Data* cur = Find(k.first);
	if (cur == nullptr)
		return false;
	cur->_state = DELETE;
	--_n;
	return true;
}

find

找对应的位置，查看是否是我们想要的值，是则返回，不是则需要往下判断，直到走到空，说明找不到，则返回nullptr。

Data* Find(const K& k)
{
	Hash hf;
	size_t hashi = hf(k) % _tables.size();
	while (_tables[hashi]._state!=EMPTY)
	{
		if (_tables[hashi]._state == EXIST && _tables[hashi]._kv.first == k)
			return &_tables[hashi];
		++hashi;
		hashi %= _tables.size();
	}
	return nullptr;
}

整体实现

namespace closehash
{
	enum State
	{
		EMPTY,
		EXIST,
		DELETE,
	};

	template<class K>
	struct HashFunc
	{
		size_t operator()(const K& k)
		{
			return (size_t)k;
		}
	};
	
	/*struct HashFuncString
	{
		size_t operator()(const string& k)
		{
			return k[0];
		}
	};*/

	template<>
	struct HashFunc<string>
	{
		size_t operator()(const string& k)
		{
			size_t hash = 0;
			for (auto& ch : k)
			{
				hash += ch;
			}
			return hash;
		}
	};

	template<class K, class V>
	struct HashData
	{
		pair<K, V> _kv;
		State _state = EMPTY;
	};

	template<class K, class V, class Hash = HashFunc<K>>
	class HashTable
	{
		typedef HashData<K, V> Data;
	public:
		HashTable()
		{
			_tables.resize(10);
		}

		bool Insert(const pair<K, V>& kv)
		{
			if (Find(kv.first) != nullptr)
				return false;
			if (_n * 10 / _tables.size() >= 7)
			{
				HashTable<K, V, Hash> tmp;
				tmp._tables.resize(2 * _tables.size());
				for (auto& e : _tables)
				{
					if (e._state == EXIST)
					{
						tmp.Insert(e._kv);
					}
				}
				_tables.swap(tmp._tables);
			}

			Hash hf;
			size_t hashi = hf(kv.first) % _tables.size();

			//线性探测
			while (_tables[hashi]._state == EXIST)
			{
				hashi++;
				hashi %= _tables.size();
			}

			_tables[hashi]._kv = kv;
			_n++;
			_tables[hashi]._state = EXIST;

			return true;
		}

		Data* Find(const K& k)
		{
			Hash hf;
			size_t hashi = hf(k) % _tables.size();
			while (_tables[hashi]._state!=EMPTY)
			{
				if (_tables[hashi]._state == EXIST && _tables[hashi]._kv.first == k)
					return &_tables[hashi];
				++hashi;
				hashi %= _tables.size();
			}
			return nullptr;
		}
		
		bool Ereas(const K& k)
		{
			Data* cur = Find(k.first);
			if (cur == nullptr)
				return false;
			cur->_state = DELETE;
			--_n;
			return true;
		}

	private:
		vector<Data> _tables;  //存储数据的空间
		size_t _n = 0;  //进去的数有多少
	};
}

2.开散列(哈希桶)

实现原理：冲突位置，将对应位置加一个链表，冲突就挂到链表上(这也是stl不实现双向迭代器的理由)

缺点：链表太长会出现问题

优点：冲突间不会相互影响

哈希桶的实现

节点元素

其实就是所谓的链表节点

template<class K, class V>
struct HashNode
{
	pair<K, V> _kv;
	HashNode<K, V>* _next;
};

哈希表框架

向量中存储链表节点地址，冲突的节点被挂起即可

template<class K, class V, class Hash = HashFunc<K>>
class HashTable
{
	typedef HashNode<K, V> Node;	
private:
	vector<Node*> _table;
	size_t _n = 0;
};

insert

插入的逻辑其实就是：如果找到了地址，新节点的next指向表的下一个，表里填入新节点地址

size_t hashi = Hash()(kv.first) % _n;
Node* newnode = new Node(kv);
newnode->_next = _table[hashi];
_table[hashi] = newnode;
_n++;

因为如果不扩容，可能一个链表会很长一串，那么查找的效率就低了，那么我们规定负载因子一般取1.0；同样如果有重复的值，那么不需要插入，直接返回false；扩容的思想和上面基本一致，这里不多赘诉。

bool Insert(const pair<K, V> kv)
{
	if (Find(kv.first) != nullptr)
		return false;
	if (_n == _table.size())
	{
		HashTable<K, V, Hash> tmp;
		tmp._table.resize(2 * _table.size(),nullptr);
		for (auto cur : _table)
		{
			while (cur)
			{
				tmp.Insert(cur->_kv);
				cur = cur->_next;
			}
		}
		_table.swap(tmp._table);
	}

	size_t hashi = Hash()(kv.first) % _table.size();
	Node* newnode = new Node(kv);
	newnode->_next = _table[hashi];
	_table[hashi] = newnode;
	_n++;
	return true;
}

关于释放空间，对于闭散列，其实不需要手动释放，因为析构函数直接释放vector结构。不过我们现在的vector中存放的是节点，这些节点是需要被释放。

~HashTable()
{
	for (int i = 0; i < _table.size(); i++)
	{
		Node* cur = _table[i];
		while (cur)
		{
			Node* next = cur->_next;
			delete cur;
			cur = next;
		}
		_table[i] = nullptr;
	}
}

这样的设计其实瑕疵很大，因为我们不仅插入实现要创造新节点，而且扩容时也创建了新节点，析构也是依次释放节点。时间效率低。我们是否可以直接将原有节点转到新表中呢？

我们只需要开辟一个新的vector，随后将原先表中的值依次遍历的存到新表中，最后交换一下表的地址，这样就能达到节省拷贝时间和析构时间的目的了。

bool Insert(const pair<K, V> kv)
{
	if (Find(kv.first) != nullptr)
		return false;
	if (_n == _table.size())
	{
		vector<Node*> newTable;
		newTable.resize(2 * _table.size(),nullptr);
		for (int i = 0; i < _table.size(); i++)
		{
			Node* cur = _table[i];
			while (cur)
			{
				Node* next = cur->_next;
				size_t hashi = Hash()(cur->_kv.first) % newTable.size();
				cur->_next = newTable[hashi];
				newTable[hashi] = cur;
				cur = next;
			}
			_table[i] = nullptr;
		}
		_table.swap(newTable);
	}

	size_t hashi = Hash()(kv.first) % _table.size();
	Node* newnode = new Node(kv);
	newnode->_next = _table[hashi];
	_table[hashi] = newnode;
	_n++;
	return true;
}

find

Node* Find(const K& k)
{
	size_t hashi = Hash()(k) % _table.size();
	Node* cur = _table[hashi];
	while (cur)
	{
		if (cur->_kv.first == k)
			return cur;
		else
			cur = cur->_next;
	}
	return nullptr;
}

Erase

删除链表节点有些时候需要前驱，所以不能复用find函数

bool Erase(const K& k)
{
	size_t hashi = Hash()(k) % _table.size();
	Node* cur = _table[hashi];
	Node* prev = nullptr;
	while (cur)
	{
		if (cur->_kv.first == k)
		{
			if (cur == _table[hashi])
				_table[hashi] = cur->_next;
			else
				prev->_next = cur->_next;
			delete cur;
			_n--;
			return true;
		}
		prev = cur;
		cur = cur->_next;
	}
	return false;
}

保持表的大小为素数，这样表的冲突会减少。所以stl中会有存储素数的表，扩容的大小就按照该表中的值进行扩容。