文章目录
- 一、文件外与文件内排序
- 二、非比较排序之计数排序
- 1.绝对映射
- 2.相对映射
- 3.代码实现
- 三、排序的稳定性
一、文件外与文件内排序
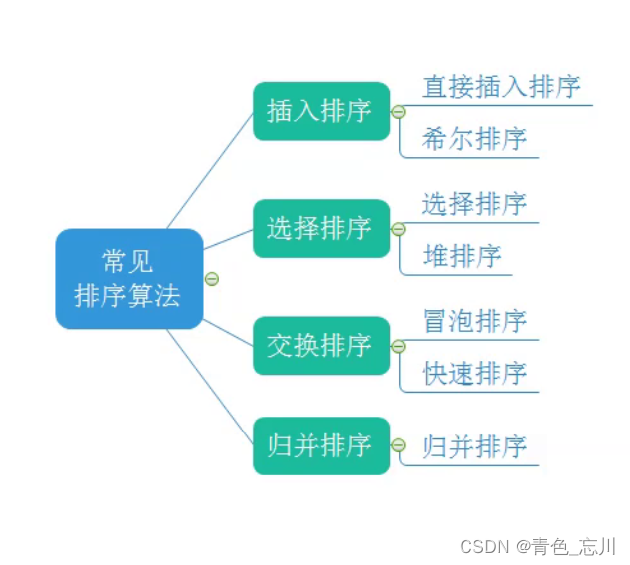
如下图所示是我们常见的的排序算法,也是我们已经使用代码实现过的
上面这七种排序算法我们都可以称之为文件内排序。但是归并排序比较特殊,他也可以称之为文件外排序。
上面的所有算法中只有归并排序可以实现文件外排序。文件外排序是因为数据量太大,比如有500G的数据,内存放不下,就需要再磁盘中去排序,而归并可以将500G的文件分为250G和250G。这样一直递归下去。当然这样是比较麻烦的。我们一般不这样做
我们一般是直接分成500个1G的文件。然后一个文件一个文件的排序。最后再归并。
关于文件外排序,上面的就是大致的思路。关于文件外排序的实现,后面会详细讲解
二、非比较排序之计数排序
非比较排序一般有下面三种
1.计数排序
2.基数排序
3.桶排序
事实上,基数排序和桶排序基本上不使用。一般只使用计数排序
1.绝对映射
计数排序的基本思想是先开辟一个数组,然后将数据全部遍历一遍,每遇到一个数再对应的下标位置上加一。最后按顺序打印出来即可
这样他的时间复杂度是O(N)
但是这样也存在一些缺陷。比如没有负的下标。无法统计负数。如果数据都处于一个较大值。比如一亿。我们直接开辟空间实在是太过于浪费了。而这种绝对映射就不太适合了
2.相对映射
绝对映射存在的一些问题,起始我们可以通过一个相对值来解决掉。我们先遍历一遍数组,选出最大值和最小值,然后开辟最大减去最小然后加一的空间大小。然后对于下标,我们将数据值减去最小值就是相对的映射了。这样一来就可以优化数据较大时候或者为负数的情况了
虽然已经有了优化,但是其实还是存在一些问题的。
1.他适合范围集中,且范围不大的整型数组排序
2.不适合范围分散或非整形的排序,如字符串、浮点数
3.代码实现
//计数排序
void CountSort(int* a, int n)
{
int i = 0;
int max = a[0], min = a[0];
for (i = 0; i < n; i++)
{
if (max < a[i])
{
max = a[i];
}
if (min > a[i])
{
min = a[i];
}
}
int range = max - min + 1;
int* CountA = (int*)calloc(range, sizeof(int));
if (CountA == NULL)
{
perror("calloc fail");
return;
}
for (i = 0; i < n; i++)
{
CountA[a[i] - min]++;
}
int j = 0;
for (i = 0; i < range; i++)
{
while (CountA[i]--)
{
a[j++] = i + min;
}
}
free(CountA);
}
三、排序的稳定性
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
简单来说就是;相等不换就是稳定的
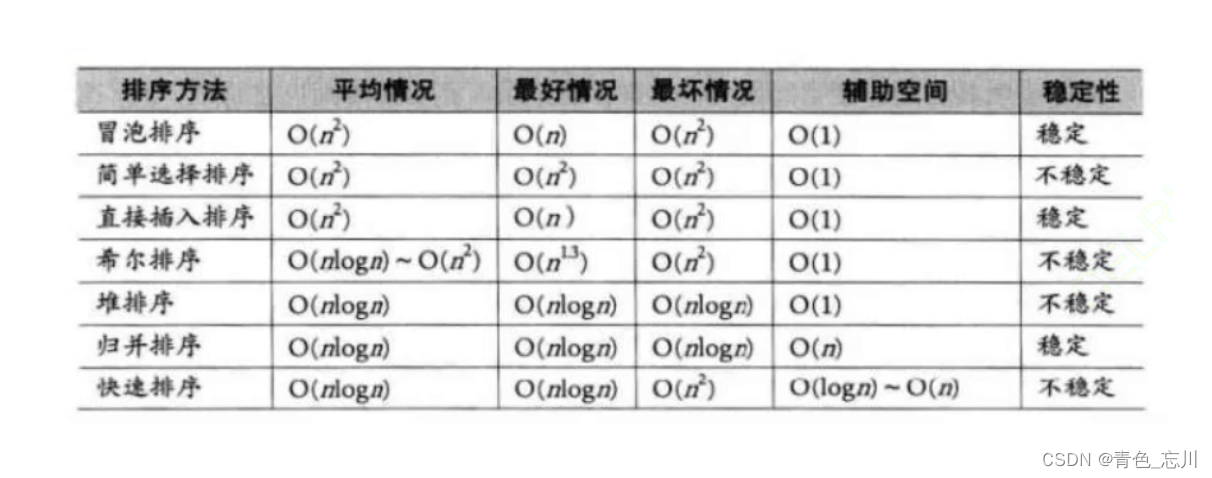
1.冒泡排序:对于冒泡排序,他是稳定的,因为他可以做到相等不换
2.简单选择排序:他是不稳定的,反例如下:当出现下面的数据时:[2,2,1…],我们由于需要选择最小的数1,当1和第一个2交换后,已经改变了顺序。所以不稳定
3.直接插入排序:是稳定的,可以做到相等不换
4.希尔排序:他是不稳定的,因为相同的数据可能会分到不同的组中
5.堆排序:不稳定,比如这个堆[9,9,8,7],他就是不稳定的
6.归并排序:稳定,因为他可以做到相等不换,我们之前的写的是不稳定的,但是再归并的代码中加上一个等于号就稳定了,就可以保证相等的时候,让左边的先下来
7.快速排序:不稳定。当数据为[5,5,5,5,5,4,5,5]时不稳定








![Vue中 引入使用 patch-package 为依赖打补丁 (以修改 vue-pdf 打包后 [hash].worker.js 路径问题为例)](https://img-blog.csdnimg.cn/5e1eeb3ab60b4e89942d3d47a72c1d71.png#pic_center)