质数

质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。

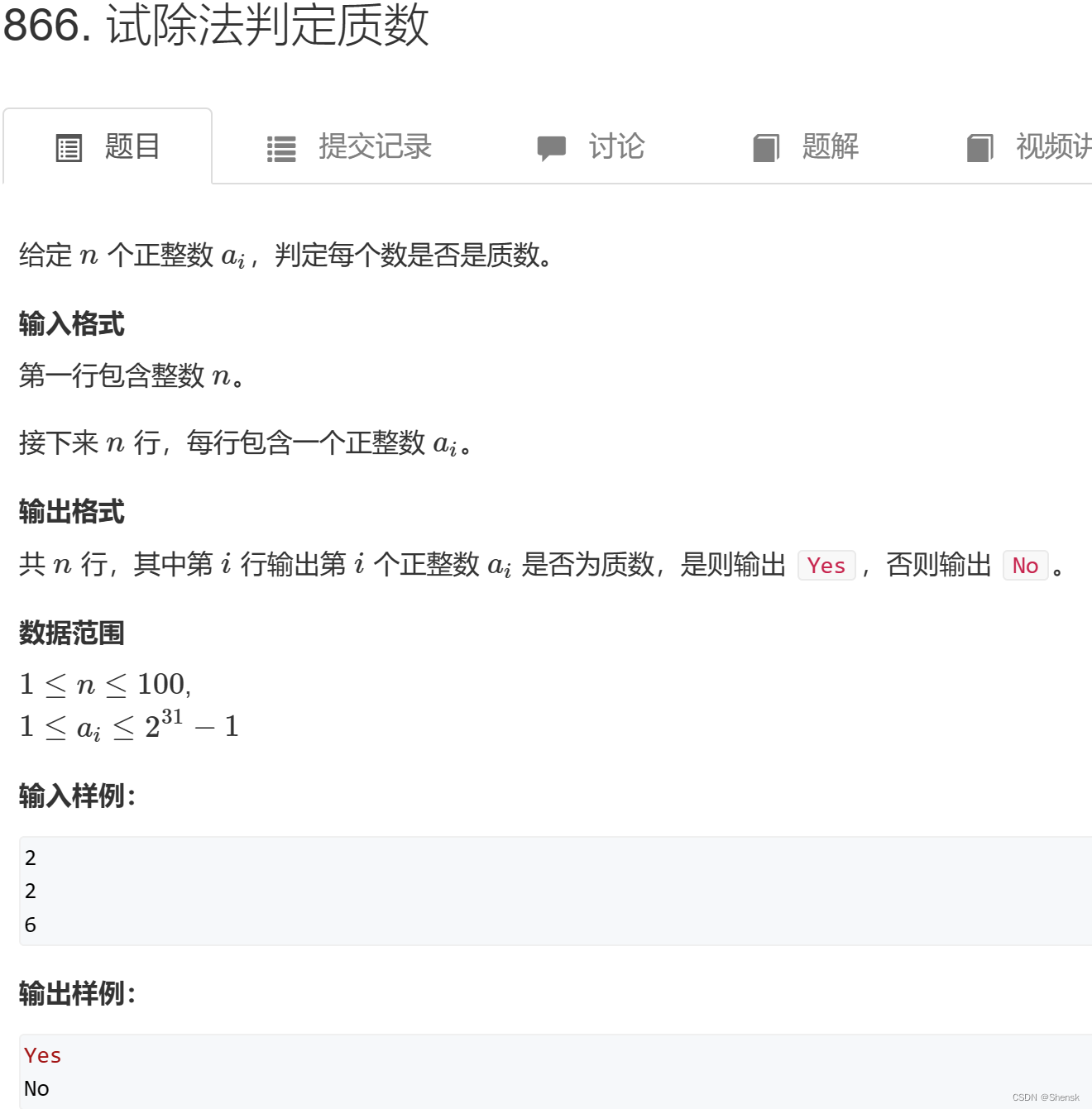
试除法判定质数

你会发现如果说一个数要分成两个数相乘的话，那么这两个数肯定都是成对出现的，有一大一小的相对关系。因此不需要从2遍历到n，循环的时候应该这样去写：

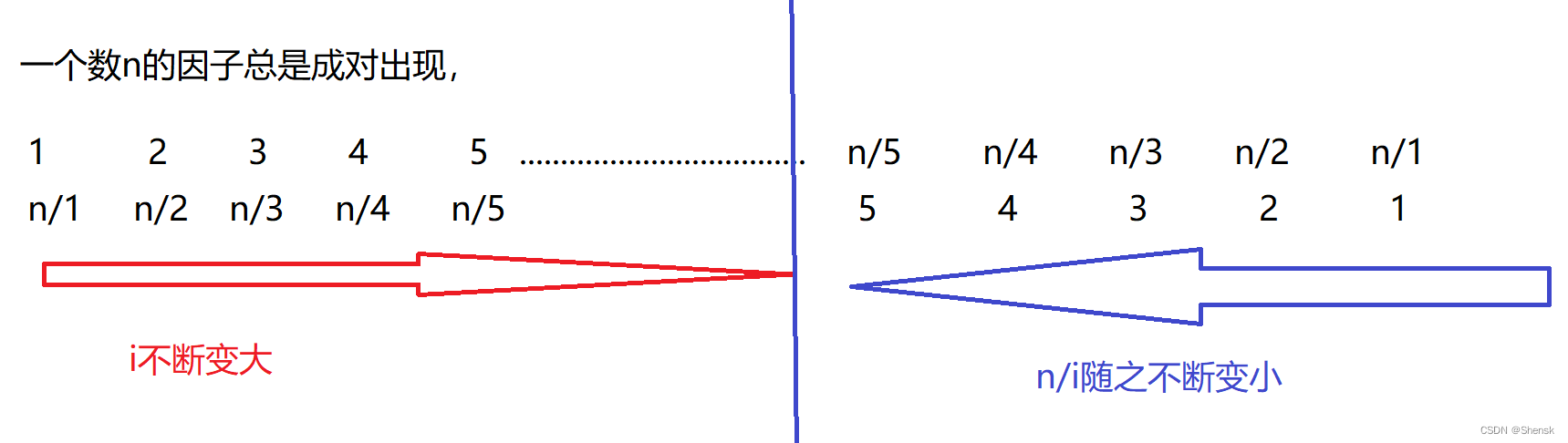
for (int i=2;i<=n/i;i++)

经典例题

luck
在这里插入图片描述

#include <stdio.h>
#include <stdbool.h>
int n;
bool is_prime(int num)
{
    if (num<2)
    {
        return false;
    }
    for (int i=2;i<=num/i;i++)
    {
        if (num%i==0)
        {
            return false;
        }
    }
    return true;
}
int main()
{
    scanf("%d",&n);
    for (int i=0;i<n;i++)
    {
        int num=0;
        scanf("%d",&num);
        if (is_prime(num)==true)
        {
            printf("Yes\n");
        }
        else
        {
            printf("No\n");
        }
    }
    return 0;    
}

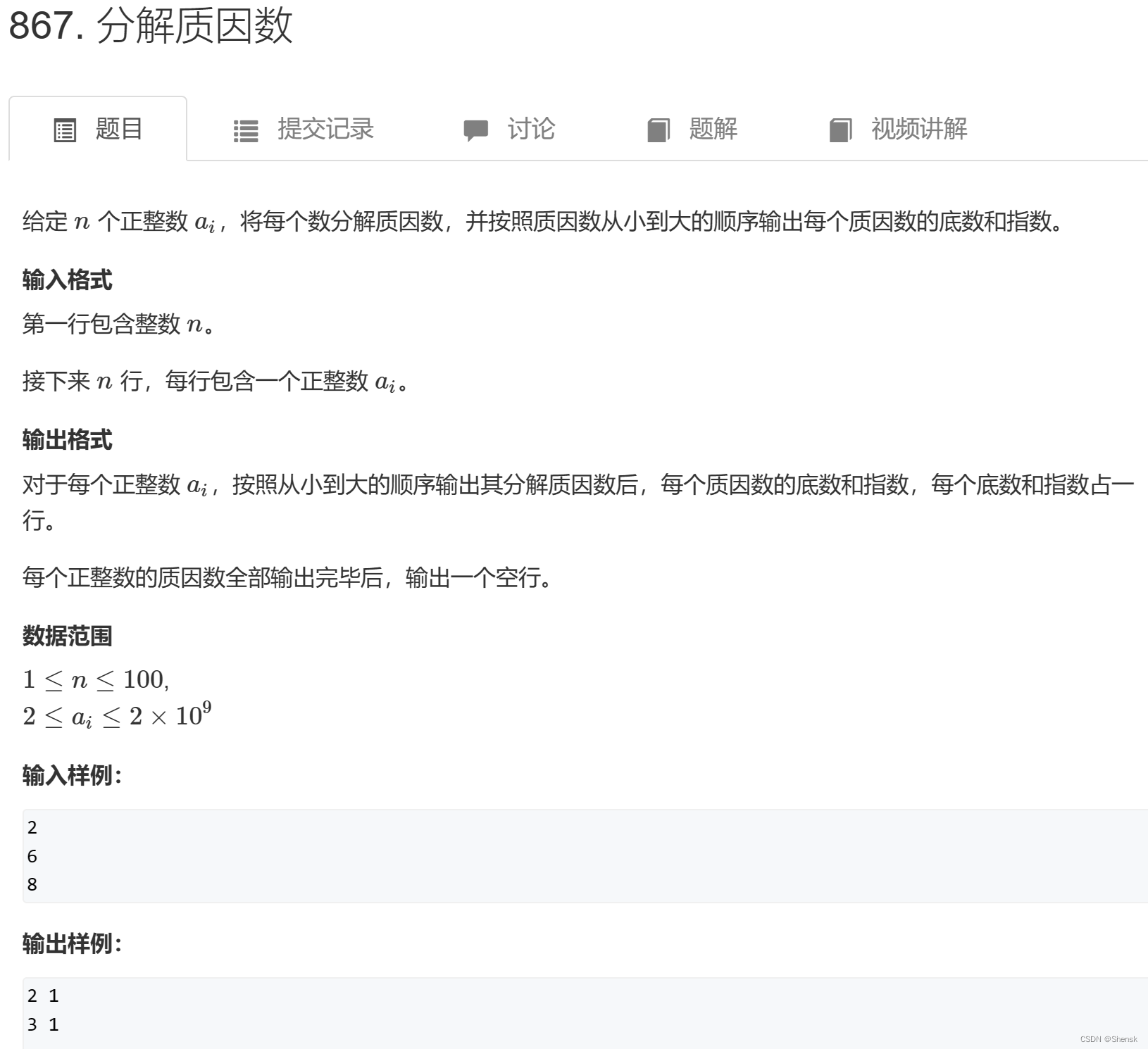
分解质因数

对于分解质因数而言，每个质因数都有底数和指数，这两个概念必须得了解清楚
首先必须得知道一点性质：对于一个数n而言，大于根号n的质因数有的话也只有一个，如果但凡出现两个以上的话，那么他们相乘就会大于n。所以我们先考虑是因数小于等于根号n的情况。那所以for循环的话就这样写：

for (int j=2;j<=x/j;j++)

然后上面这个for循环相当于就是去遍历一下小于等于根号n的每一个数，然后这个数如果能被整除（并且很容易就知道，最开始被整除的那个数必定是一个质数）的话，那么我们就在这个原数当中不断地去剔除这个质数，在这个过程当中指数不断的去++。然后直到这个质数在原数当中被剔除的不能再剔除了，这时候首先输出一对底数与指数，然后再继续进行for循环，要注意的是，由于在不断的剔除质数的过程当中，这个原数也自己在不断的坍塌缩小，所以说这个for循环已经变得更加容易结束。

for (int j=2;j<=x/j;j++)
{
    if (x%j==0)
    {
        int s=0;
        while(x%j==0)
        {
            s++;
            x/=j;
        }
        printf("%d %d\n",j,s);
    }
}

然后我们再去判断一下大于根号n的那个范围内是否存在那么孤独的一个质因数，可能存在，也有可能不存在。这时候就拿已经被削弱的原数去和1比较一下，如果大于1的话，那这时候就说明还存在着一个质因数,注意：一定是要大于1才可以。1的话本身并不是一个质因数。

if (x>1)
{
    printf("%d %d\n",x,1);
}

经典例题

luck
在这里插入图片描述

#include <stdio.h>
int n;
void divide(int num)
{
    for (int i=2;i<=num/i;i++)
    {
        if (num%i==0)
        {
            int s=0;
            while(num%i==0)
            {
                s++;
                num/=i;
            }
            printf("%d %d\n",i,s);
        }
    }
    if (num>1)
    {
        printf("%d %d\n",num,1);
    }
}
int main()
{
    scanf("%d",&n);
    for (int i=0;i<n;i++)
    {
        int num=0;
        scanf("%d",&num);
        divide(num);
        printf("\n");
    }
    return 0;
}

埃式筛法筛质数

首先如果要筛选质数的话，需要开两个数组，第一个数组就是用来存放筛选出来的质数，第二个数组是一个布尔数组，它的下标就是用来记录筛选的范围(如从1到n当中筛选质数），然后它的内容也就是布尔值，就是用来记录当前下标值这个数是不是质数

bool st[N];//默认为false表示里面的数默认全部是质数
int primes[N];
int cnt;

这个算法的核心就在于首先对于筛选范围进行一次for遍历，对于每一次for循环，去判断一下当前这个数是不是一个质数，如果说当前这个数不是质数，就什么都不用去处理；如果当前这个数被标识为是一个质数的话，我就先把它加入到结果数组当中，然后这个质数的倍数肯定不可能将会再是质数，说就把这个质数的倍数质数标识情况给他更新一下，也就是都给他计为不是质数，到时候在后面遍历到他们的时候就什么都不用去处理。

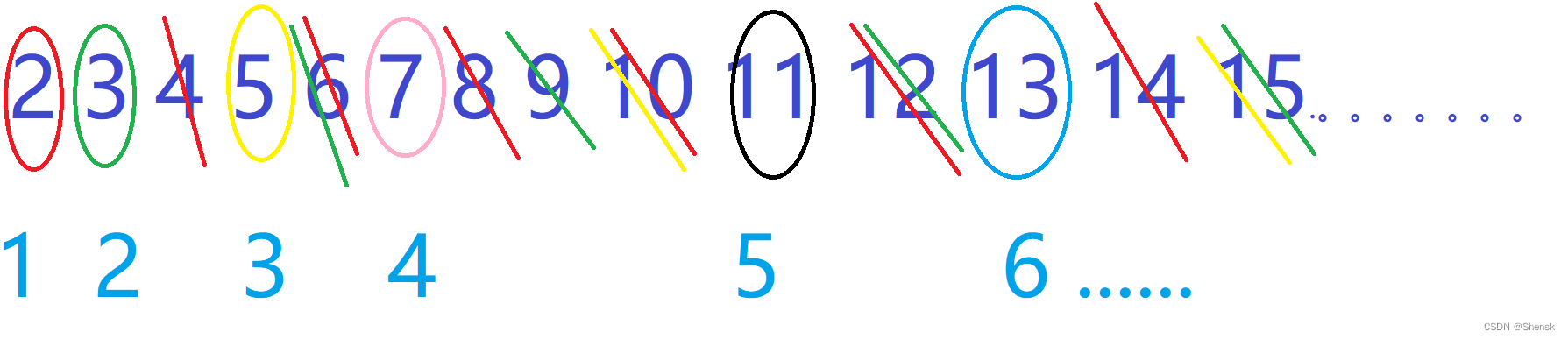
经典例题

luck
在这里插入图片描述

#include <stdio.h>
#include <stdbool.h>
#define N 1000010
bool st[N];//默认为false表示里面的数默认全部是质数
int primes[N];
int cnt;
int n;
int main()
{
    scanf("%d",&n);
    for (int i=2;i<=n;i++)
    {
        if(st[i]==false)
        {
            primes[cnt++]=i;
            for (int j=i+i;j<=n;j+=i)
            {
                st[j]=true;
            }
        }
        
    }
    printf("%d\n",cnt);
    return 0;
}

线性筛法筛质数

上面这种埃式筛法会发现有一个明显的不好的地方就在于，对于好几个数都是给他筛除掉了多次，是给他重复删除了，这个重复操作是没有必要的。于是再进行一些优化就有了线性筛法。线性筛法的最核心的地方就在于：就是让一个合数的最小质因数去筛除掉它，必须是要让一个合数的最小质因数去筛除它，这么一来的话每一个合数都只被筛除掉了一次，就没有重复操作了。
仍然是与刚才的算法一样，先开两个数组，一个数组就是用来记录一下筛选出来的质数，另一个数组就是来记录一下每一个数的是否是质数情况

int primes[N];
int cnt;
bool st[N];

首先也是与刚才上面一样对整个筛选范围进行一次for循环遍历，然后如果说这个数是质数的话，把他加入到结果数组当中，然后接下来的操作就是无论你这个数是不是质数都必须要进行的一个操作

for (int i=2;i<=n;i++)
{
    if (st[i]==false)
    {
        primes[cnt++]=i;
    }
    //....
}

下来就是整个算法最为关键的地方，因为线性筛法的话就是让一个合数的最小质因数去筛除掉它，而不是用其他的数字。这时候就去遍历一下这个结果数组（里面存放的就是已经被筛选出来的质数，且是从小到大），然后把这些质数乘上倍数i所得到的一个合数就给他标记为不是质数，然后这边最为关键的一个地方就在于，当去修改完一个合数的质数标记后，就去判断一下这个i能否可以整除当前这个结果数组当中的质数，如果说可以被整除的话，那这时候就应该被停下来:

for (int i=2;i<=n;i++)
{
    if (st[i]==false)
    {
        primes[cnt++]=i;
    }
    for (int j=0;primes[j]<=n/i;j++)
    {
        st[primes[j]*i]=true;
        if (i%primes[j]==0)
        {
            break;
        }
    }
}

最后解释一下上面代码当中第二个for循环的结束条件为什么是这样子的，你可以把它理解成为了使得primes[j] 最后呈上一个这个数值i必须是要在筛选的范围之内，那会不会这个j会可能超出这个cnt呢？实际上是不会的。

for (int j=0;primes[j]<=n/i;j++)

经典例题

luck
在这里插入图片描述

#include <stdio.h>
#include <stdbool.h>
#define N 1000010
bool st[N];//默认为false表示里面的数默认全部是质数
int primes[N];
int cnt;
int n;
int main()
{
    scanf("%d",&n);
    for (int i=2;i<=n;i++)
    {
        if (st[i]==false)
        {
            primes[cnt++]=i;
        }
        for (int j=0;primes[j]<=n/i;j++)
        {
            st[primes[j]*i]=true;
            if (i%primes[j]==0)
            {
                break;
            }
        }
    }
    printf("%d\n",cnt);
    return 0;
}