2023牛客五一集训派对day1部分题解

news2024/10/6 14:27:41

F Infinite String Comparision

F	Infinite String Comparision

题目描述

给你两个可以无限复制自身的字符串 a, b。请你判断其无限复制后两字符串的字典序大小。

解题思路

我们可以设 s1 = a + b, s2 = b + a

则有:

$s1^{\infty }=ababab...$

$s2^{\infty}=bababa...$

通过观察可见 s1, s2 包含 $a^{\infty}$ 和 $b^{\infty}$ ，于是我们比较 s1, s2 相当于比较 $s1^{\infty}$ 和 $s2^{\infty}$

此时可以把 a 和 b 都看作一位数(类似于十进制), 那么我们可以把字典序的比较看作每一位上的比较, 也就是说此时比较的就是各位的数(a, b)乘上对应位的权值

之后我们再设:

$s1^{\infty}$ 中 $a^{\infty}$ 对应的权值总和为 sum1, $b^{\infty}$ 对应的权值总和为 sum2

$s2^{\infty}$ 中 $a^{\infty}$ 对应的权值总和为 sum2, $b^{\infty}$ 对应的权值总和为 sum1

具体解释一下:

sum1 对应 2k - 1 位 k = 1, 2, 3...

sum2 对应 2k 位 k = 1, 2, 3...

按 x 进制表示则有位数越小, 位数就越考前, 权值也就越大

s1 - s2 = $s1^{\infty}$ - $s2^{\infty}$ = (sum1 * $a^{\infty}$ + sum2 * $b^{\infty}$ ) - (sum2 * $a^{\infty}$ + sum1 * $b^{\infty}$ )

s1 - s2 = (sum1 - sum2) * ( $a^{\infty}$ - $b^{\infty}$ )

则有 sum1 - sum2 > 0

则 s1 - s2 可以表示 $a^{\infty}$ - $b^{\infty}$ 的字典序, 故直接比较 s1 - s2 即可

代码示例

#include<bits/stdc++.h>
using namespace std;

string a, b;

int main(){
    while(cin >> a >> b){
        string sa = a + b;
        string sb = b + a;
        if(sa < sb) cout << "<\n";
        if(sa > sb) cout << ">\n";
        if(sa == sb) cout << "=\n";
    }
}

J Easy Integration

J	Easy Integration

题目描述

求 $\int_{0}^{1}(x - x^{2})^{n}dx$ 在取 mod = 998244353 之后的结果

解题思路

分部积分推导过程

$\int_{0}^{1}(x - x^{2})^{n}dx=(n!)^{2}/(2 * n + 1)!$

这里提前预处理一下阶乘, 注意取逆元就可以了

代码示例

#include<bits/stdc++.h>
using namespace std;

#define int long long

const int N = 2e6 + 10;
const int mod = 998244353;
int n;
int a[N];

int q_pow(int a, int b, int mod){
    int cnt = 1;
    while(b){
        if(b & 1) cnt = cnt * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return cnt;
}

int fermat(int a, int mod){
    return q_pow(a, mod - 2, mod);
}

signed main(){
    a[1] = 1;
    for(int i = 2; i <= 2e6 + 1; i++){
        a[i] = a[i - 1] * i;
        a[i] %= mod;
    }  
    while(cin >> n){
        int up = q_pow(a[n], 2, mod);
        int down = a[2 * n + 1];
        cout << up * fermat(down, mod) % mod << '\n';
    }
}

A B-Suffix Array

A	B-Suffix Array

题目大意

给出一个只含有 ' a ' 和 ' b ' 的字符串，再给出 B 数组的构造方法如下：对于每个位置 i 来说

如果存在一个位置 j ，使得 j < i 且 s[ j ] == s[ i ] ，则 b[ i ] = min(i - j)
否则 b[ i ] = 0

现在需要对字符串的每个后缀构造 B 数组，并按照字典序排序

解题思路

首先我们要了解一下后缀数组, 如果您已知晓可以直接跳到分析部分

后缀数组

一句话概括: 一个字符串的所有后缀按字典序排序后的结果, 就是这一个字符串的后缀数组。

str: 需要处理的字符串(长度为len)
suffix[i]: str下标为 i ~ len 的连续子串(即后缀)
rank[i]: suffix[i]在所有后缀中的排名
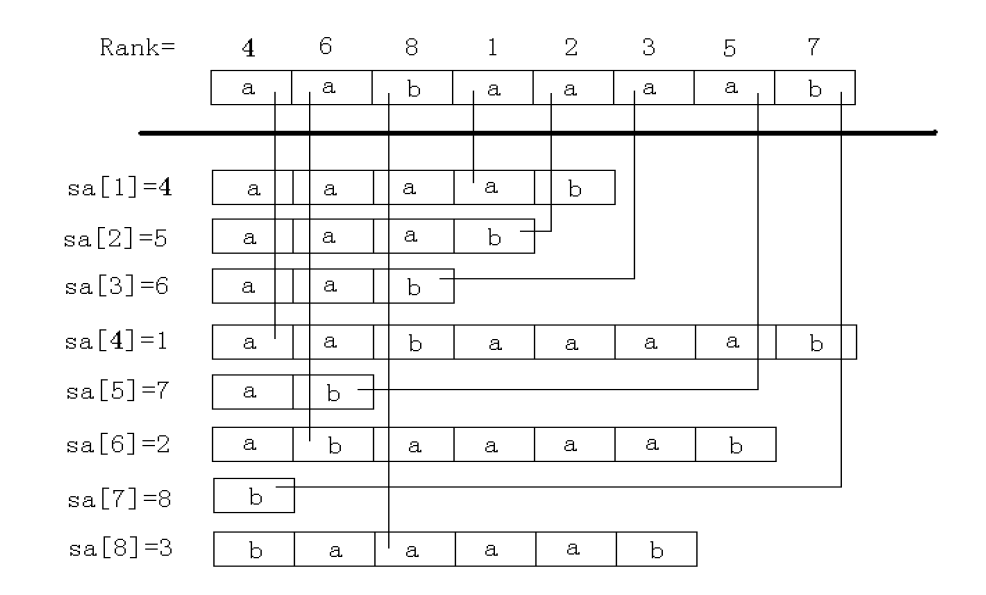
sa[i]: 表示将所有后缀排序后第 i 小的后缀的编号, 也是所说的后缀数组, 满足 suffix[sa[1]] < suffix[sa[2]] …… < suffix[sa[len]], 即排名为 i 的后缀为 suffix[sa[i]]
满足一个特殊性质 rank[sa[i]] = sa[rank[i]] = i

这就是Rank和SA

用倍增方法求后缀数组 $O(Nlog^{2}N)$

对于一个后缀 suffix[i], 如果想直接得到 rank 比较困难，但是我们可以对每个字符开始的长度为 $2^{k}$ 的字符串求出排名，k 从 0 开始每次递增 1 (每递增 1 就成为一轮)，当 $2^{k}$ 大于 len 时, 所得到的序列就是 rank, 此时 sa 也可以间接计算出来

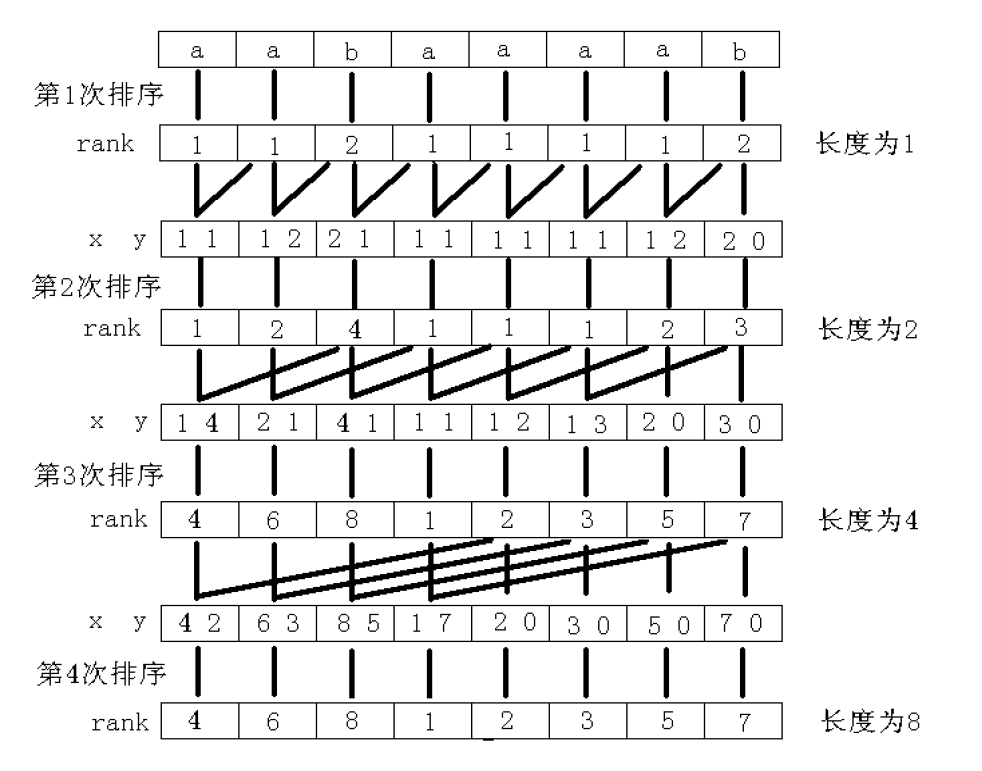
首先对字符串 str 的所有长度为 1 的子串, 即每个字符进行排序, 得到排序后的编号数组 $sa_{1}$ 和排名数组 $rank_{1}$

简单概括一下: 对于长度为 len 的字符串 str, 第 k 轮 $substr(i, 2^{k})$ 可以看成 $substr(i, 2^{k - 1})$ 和 $substr(i + 2^{k - 1}, 2^{k})$ 的拼接, 而这两个 substr 是我们之前计算过的, 于是就可以看成两个关键字进行比较, 再把此轮的每个位置的双关键字进行比较重新排名就是这一轮的 rank

就像一个两位数的比较

构造最长公共前缀 - height

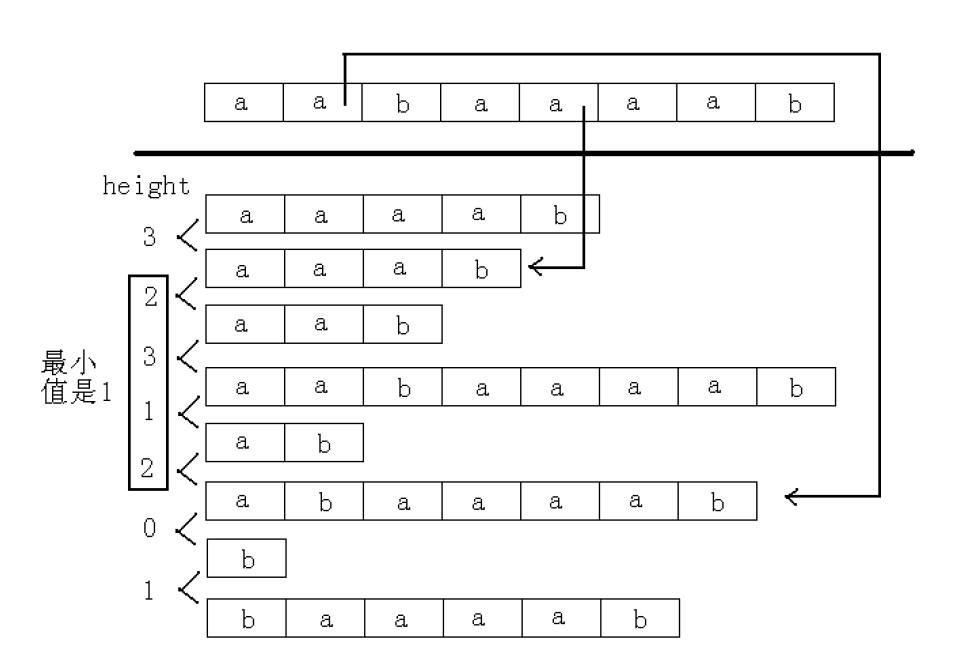
heigth[i]: 表示 suffix[sa[i]] 和 suffix[sa[i - 1]] 的最长公共前缀, 也就是排名相邻的两个后缀的最长公共前缀
h[i]: 等于 height[rank[i]], 也就是后缀 suffix[i] 和它前一名的后缀的最长公共前缀
而两个排名不相邻的最长公共前缀定义为排名在它们之间的 height 的最小值

这就是Height

设 suffix[k] 是排在 suffix[i - 1] 前一名的后缀, 则它们的最长公共前缀是 h[i - 1], 都去掉第一个字符, 就变成 suffix[k + 1] 和 suffix[i], 如果 h[i - 1] = 0 或 1, 那么 h[i] ≥ 0 显然成立, 否则 h[i] ≥ h[i - 1] - 1(去掉了原来的第一个, 其他前缀一样相等), 所以 suffix[i] 和在它前一名的后缀的最长公共前缀至少是 h[i - 1] - 1 进而可以求出来 height[i]

参考资料:

OI Wiki 后缀数组

五分钟搞懂后缀数组！后缀数组解析以及应用(附详解代码)