前置知识

统计

假设数据集$\mathbf{X}\in {\mathbb{R}}^{n\times m}$,其中$n$表示样本数量，$m$表示特征个数

均值$\bar{\mathbf{X}}=\frac{1}{n}{\mathbf{e}}^T\mathbf{X}=\frac{1}{n}{\sum }_{i=1}^n{\mathbf{X}}_i$(其中$\mathbf{e}$为全$1$向量,${\mathbf{X}}_i$是行向量)
协方差$cov(\mathbf{X})=\frac{1}{n-1}{\left(\mathbf{X}-\bar{\mathbf{X}}\right)}^T\left(\mathbf{X}-\bar{\mathbf{X}}\right)$

补充说明：
1.这里用$n-1$和$n$都行，因为最后只要特征向量，而不需要特征值，$\mathbf{A}x=\lambda x\Rightarrow (k\mathbf{A})x=\left(k\lambda \right)\mathbf{x}$
2.其实不能直接$\mathbf{X}-\bar{\mathbf{X}}$,因为维度对不上，这里就当作能广播

投影

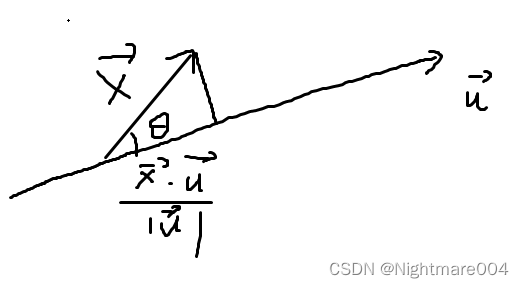
将$\mathbf{x}$投影到$\mathbf{u}$
$$\Vert \mathbf{x}\Vert \cos \theta =\Vert \mathbf{x}\Vert \frac{\mathbf{x}\cdot \mathbf{u}}{\Vert \mathbf{x}\Vert \Vert \mathbf{u}\Vert }=\frac{\mathbf{x}\cdot \mathbf{u}}{\Vert \mathbf{u}\Vert }$$
如果$\mathbf{u}$是单位向量，则投影简化为$\mathbf{x}\cdot \mathbf{u}$

PCA

步骤

1.减均值
$$\hat{\mathbf{X}}=\mathbf{X}-\bar{\mathbf{X}}=\mathbf{X}-\frac{1}{n}\mathbf{e}{\mathbf{e}}^T\mathbf{X}=\left(\mathbf{I}-\frac{1}{n}\mathbf{e}{\mathbf{e}}^T\right)\mathbf{X}$$
（其实不能直接$\mathbf{X}-\bar{\mathbf{X}}$,因为维度对不上，这里就当作能广播，后面两个等号维度是对的上的）

减均值之后，均值为$0$
这里也可以继续除以标准差

2.计算协方差矩阵
$$cov\left(\hat{\mathbf{X}}\right)=\frac{1}{n-1}{\hat{\mathbf{X}}}^T\hat{\mathbf{X}}\in {\mathbb{R}}^{m\times m}$$
这里因为均值为$0$,所以不用再减去$\bar{\mathbf{X}}$
3.计算协方差矩阵特征值与特征向量
不妨假设计算之后的特征值${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_m$
对应的单位特征向量${\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_m$
4.选择前$k$大的特征值对应的特征向量
设$\mathbf{V}=\left({\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_k\right)\in {\mathbb{R}}^{m\times k}$
5.投影
$$\mathbf{Y}=\hat{\mathbf{X}}\mathbf{V}\in {\mathbb{R}}^{n\times k}$$

原理

最大方差理论

信号处理中认为信号具有较大的方差，噪声有较小的方差
因此我们认为，最好的$k$维特征是将样本转换为$k$维后，每一维上的样本方差都很大

设$\hat{\mathbf{X}}$为减去均值后的数据集
先从$k=1$开始，不妨假设投影到$\mathbf{u}$,投影后为$\hat{\mathbf{X}}\mathbf{u}$
投影之后的均值依然为$0$，（${\mathbf{e}}^T\hat{\mathbf{X}}=0\Rightarrow {\mathbf{e}}^T\left(\hat{\mathbf{X}}\mathbf{u}\right)=0$）

则方差
$$\begin{array}{rl}\arg \underset{\Vert \mathbf{u}\Vert =1}{\max }{S}^2& =\frac{1}{n-1}\arg \underset{\Vert \mathbf{u}\Vert =1}{\max }{\mathbf{u}}^T{\hat{\mathbf{X}}}^T\hat{\mathbf{X}}\mathbf{u}\\ & =\arg \underset{\Vert \mathbf{u}\Vert =1}{\max }{\mathbf{u}}^{T}cov\left(\hat{\mathbf{X}}\right)\mathbf{u}\end{array}$$
熟悉的话就知道这个是瑞利商，不熟悉可以用拉格朗日乘数法，或者特征值分解
最后得到$\mathbf{u}$为${\hat{\mathbf{X}}}^T\hat{\mathbf{X}}$的最大特征值对应的特征向量

为了方便，设刚刚得到的$\mathbf{u}$为${\mathbf{u}}_1$
现在需要找${\mathbf{u}}_2$,使得投影后方差最大，并且${\mathbf{u}}_2$与${\mathbf{u}}_1$正交
$$\arg \underset{\genfrac{}{}{0ex}{}{\Vert {\mathbf{u}}_2\Vert =1}{{\mathbf{u}}_1^T{\mathbf{u}}_2=1}}{\max }{\mathbf{u}}_2^{T}cov\left(\hat{\mathbf{X}}\right){\mathbf{u}}_2$$
构造拉格朗日函数
$$L\left({\mathbf{u}}_2,\lambda ,\mu \right)={\mathbf{u}}_2^{T}cov\left(\hat{\mathbf{X}}\right){\mathbf{u}}_2-\lambda \left({\mathbf{u}}_2^T{\mathbf{u}}_2-1\right)-\mu {\mathbf{u}}_1^T{\mathbf{u}}_2$$
求偏导
$$\frac{\partial L}{\partial {\mathbf{u}}_2}=2cov\left(\hat{\mathbf{X}}\right){\mathbf{u}}_2-2\lambda {\mathbf{u}}_2-\mu {\mathbf{u}}_1=0$$
注意到$cov\left(\hat{\mathbf{X}}\right){\mathbf{u}}_1={\lambda }_1{\mathbf{u}}_1$,并且协方差矩阵是个对称矩阵，有
$$\begin{array}{rl}& 2{\mathbf{u}}_1^{T}cov\left(\hat{\mathbf{X}}\right){\mathbf{u}}_2-2{\mathbf{u}}_1^T{\mathbf{u}}_2-\mu {\mathbf{u}}_1^T{\mathbf{u}}_1\\ =& 2{\lambda }_1{\mathbf{u}}_1^T{\mathbf{u}}_2-0-\mu \\ =& \mu \\ =& 0\end{array}$$
于是
$$cov\left(\hat{\mathbf{X}}\right){\mathbf{u}}_2=\lambda {\mathbf{u}}_2$$
可以得到${\mathbf{u}}_2$为$cov\left(\hat{\mathbf{X}}\right)$第二大特征值对应的特征向量

后面以此类推

https://towardsdatascience.com/principal-component-analysis-part-1-the-different-formulations-6508f63a5553
https://www.askpython.com/python/examples/principal-component-analysis
https://bagheri365.github.io/blog/Principal-Component-Analysis-from-Scratch/
https://www.python-engineer.com/courses/mlfromscratch/11_pca/
http://blog.codinglabs.org/articles/pca-tutorial.html