LeetCode 105. 从前序与中序遍历序列构造二叉树

题目描述

题目地址：105. 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

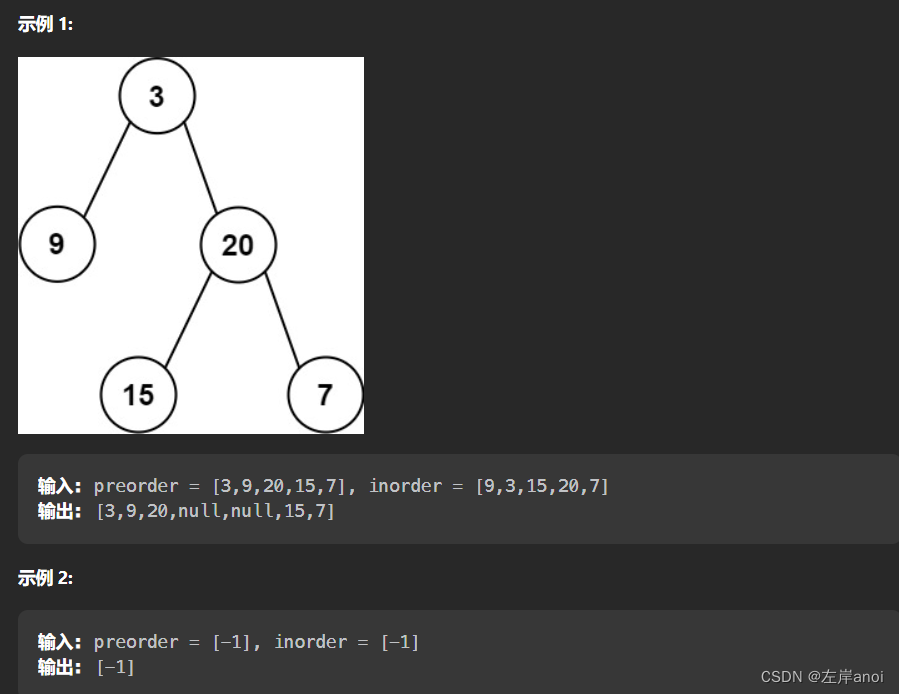
解题思路

思路一：使用递归

代码实现

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    //哈希表:哈希映射中的每个键值对，键表示一个元素（节点的值），值表示其在中序遍历中的出现位置
    unordered_map<int,int> index;
public:
    TreeNode* myBuildTree(vector<int>& preorder,vector<int>& inorder,int preorder_left,int preorder_right,int inorder_left,int inorder_right){
        if(preorder_left>preorder_right) return NULL;
        
        //2.在前序遍历preorder中确定根节点的值(中左右)
        //前序遍历中的第一个节点就是根节点
        int preorder_root=preorder_left;
        //3.根据根节点的值在中序遍历inorder中定位根节点的位置，和左右子树（左中右）
        //在中序遍历中定位根节点
        int inorder_root=index[preorder[preorder_root]];

        //先把树的根节点建立出来
        TreeNode* root=new TreeNode(preorder[preorder_root]);
        //算出左子树中的节点数目
        int left_subTree_size=inorder_root-inorder_left;

        //4.再根据左右子树在前序遍历preorder中定位左，右子树的位置（左中右
        //递归地构造左子树，并连接到根节点
        root->left=myBuildTree(preorder,inorder,preorder_left+1,preorder_left+left_subTree_size,inorder_left,inorder_root-1);
        //递归地构造右子树，并连接到根节点
        root->right=myBuildTree(preorder,inorder,preorder_left+left_subTree_size+1,preorder_right,inorder_root+1,inorder_right);

        return root;
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder){
        //1.将中序遍历inorder构造成哈希表（以便在找根节点时能够快速定位）
        //2.在前序遍历preorder中确定根节点的值(中左右)
        //3.根据根节点的值在中序遍历inorder中定位根节点的位置，和左右子树（左中右）
        //4.再根据左右子树在前序遍历preorder中定位左，右子树的位置（左中右）
        //5.继续在左右子树中重复2,3,4操作
        
        int n=preorder.size();
        //在构造二叉树的过程之前，我们可以对中序遍历的列表进行一遍扫描，就可以构造出这个哈希映射。在此后构造二叉树的过程中，我们就只需要O(1)的时间对根节点进行定位了
        for(int i=0;i<n;++i){
            index[inorder[i]]=i;
        }
        return myBuildTree(preorder,inorder,0,n-1,0,n-1);
    }
};

运行结果

参考文章：

https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/solutions/255811/cong-qian-xu-yu-zhong-xu-bian-li-xu-lie-gou-zao-9/?orderBy=most_votes

思路二：减少遍历节点数

代码实现

C++

在这里插入代码片

运行结果

参考文章：

LeetCode 106. 从中序与后序遍历序列构造二叉树

题目描述

题目地址：106. 从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

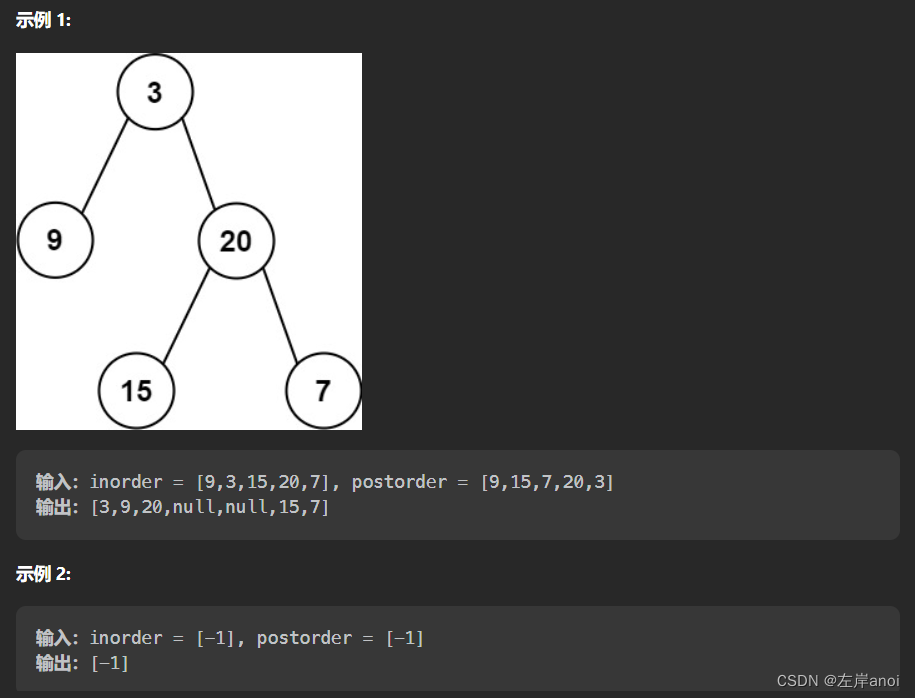
解题思路

思路一：使用递归

代码实现

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    //哈希表:哈希映射中的每个键值对，键表示一个元素（节点的值），值表示其在中序遍历中的出现位置
    unordered_map<int,int> index;
public:
TreeNode* myBuildTree(vector<int>& postorder,vector<int>& inorder,int postorder_left,int postorder_right,int inorder_left,int inorder_right){
        if(postorder_left>postorder_right) return NULL;
        
        //2.在后序遍历postorder中确定根节点的值(左右中)
        //后序遍历中的最后一个节点就是根节点
        int postorder_root=postorder_right;
        //3.根据根节点的值在中序遍历inorder中定位根节点的位置，和左右子树（左中右）
        //在中序遍历中定位根节点
        int inorder_root=index[postorder[postorder_root]];

        //先把树的根节点建立出来
        TreeNode* root=new TreeNode(postorder[postorder_root]);
        //算出左子树中的节点数目
        int left_subTree_size=inorder_root-inorder_left;

        //4.再根据左右子树在后序遍历postorder中定位左，右子树的位置（左右中）
        //递归地构造左子树，并连接到根节点
        root->left=myBuildTree(postorder,inorder,postorder_left,postorder_left+left_subTree_size-1,inorder_left,inorder_root-1);
        //递归地构造右子树，并连接到根节点
        root->right=myBuildTree(postorder,inorder,postorder_left+left_subTree_size,postorder_right-1,inorder_root+1,inorder_right);

        return root;
    }

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        //1.将中序遍历inorder构造成哈希表（以便在找根节点时能够快速定位）
        //2.在后序遍历postorder中确定根节点的值(左右中)
        //3.根据根节点的值在中序遍历inorder中定位根节点的位置，和左右子树（左中右）
        //4.再根据左右子树在后序遍历postorder中定位左，右子树的位置（左右中）
        //5.继续在左右子树中重复2,3,4操作
        
        int n=postorder.size();
        //在构造二叉树的过程之前，我们可以对中序遍历的列表进行一遍扫描，就可以构造出这个哈希映射。在此后构造二叉树的过程中，我们就只需要O(1)的时间对根节点进行定位了
        for(int i=0;i<n;++i){
            index[inorder[i]]=i;
        }
        return myBuildTree(postorder,inorder,0,n-1,0,n-1);

    }
};

运行结果

参考文章：

https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/solutions/426738/cong-zhong-xu-yu-hou-xu-bian-li-xu-lie-gou-zao-14/?orderBy=most_votes

思路二：减少遍历节点数

代码实现

C++

在这里插入代码片

运行结果

参考文章：