6 problems. ABC过, DE没想出来, F没看.
https://codeforces.com/contest/1816
A. Ian Visits Mary
分析 - AC
每次跳跃,横纵互质。
限于数据量,不能枚举。
1与任何数互质。考虑从(0,0)跳到(1,y),这一步一定合法;再从(1,y)跳到(a,b),为了让这一步合法,可以使y=a+b,这样横纵长度分别是a-1和a,合法。
交上去WA,因为忘记了过程中
0
≤
x
i
,
y
i
≤
1
0
9
0≤x_i,y_i≤10^9
0≤xi,yi≤109. a+b可能超出,b-a即可。但b-a可能是负数,此时,走另一条类似的路,出现的是a-b.
cin >> a >> b;
cout << 2 << "\n";
if (b > a) cout << 1 << ' ' << b - a << "\n";
else cout << a - b << ' ' << 1 << "\n";
cout << a << ' ' << b << "\n";
更好的分析 - AC(赛后)
打上面一段话时才发现,更简单地,让两步跳跃的线段分别横向是1,纵向是1,即经过(1,b-1).
上文只用了1次1,这里用了2次1,所以更简单。
B. Grid Reconstruction
分析 - AC
黑白详相间染色,显然
[
1
,
n
]
[1,n]
[1,n]填在
−
-
−上,
[
n
+
1
,
2
n
]
[n+1,2n]
[n+1,2n]填在
+
+
+上;且必经过的起点和终点都是
+
+
+,肯定填2n,2n-1.
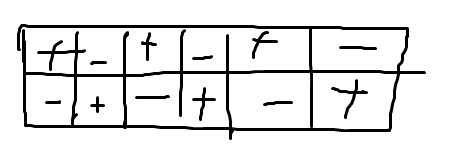
路径的不同取决于选择在哪里进入第二行。在所有路径中选择最小的,且所有数字总和为常数,显然要让各个路径的差值最小。据此,很容易解决本题。
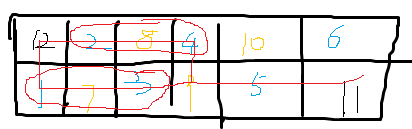
a[1][1] = 2 * n, a[2][n] = 2 * n - 1;
for (int i = 1; i <= n; ++i) {
a[(i & 1) + 1][i] = i;
}
for (int i = n + 1; i <= 2 * n - 2; ++i) {
int j = i - n + 1;
a[(i & 1) + 1][j] = i;
}
for (int i = 1; i <= 2; ++i) {
for (int j = 1; j <= n; ++j) {
cout << a[i][j] << ' ';
} cout << "\n";
}
C. Ian and Array Sorting
差分 - AC
以差分的视角,操作即,
b
i
b_i
bi和
b
i
+
2
b_{i+2}
bi+2一个加1,一个减1,即其中一个传递数字给另一个,使总和不变。
原数组单调不减,即b中所有数非负。
特别地,原数组最后两个数同加同减,是
b
n
−
1
b_{n-1}
bn−1单独加减,所以设
b
n
+
1
=
+
∞
b_{n+1}=+\infty
bn+1=+∞.
b
1
b_1
b1其实不需要非负,所以
b
1
=
+
∞
b_1=+\infty
b1=+∞.
根据
b
i
b_i
bi和
b
i
+
2
b_{i+2}
bi+2,差分数组中下标奇偶性不同的元素无法互相影响,所以按照下标奇偶性把数组分成两块。
每块中,保证总和不变,任意地传递数字,使所有数非负。总和非负便有可能。
cin >> n;
for (int i= 1; i <= n; ++i) {
cin >> a[i];
}
for (int i = n; i; --i) {
a[i] -= a[i - 1];
}
a[1] = a[n + 1] = LNF;
ll s = 0;
for (int i = 1; i <= n + 1; i += 2) s += a[i];
if (s < 0) {
cout << "no\n";
continue;
}
s = 0;
for (int i = 2; i <= n + 1; i += 2) s += a[i];
if (s < 0) {
cout << "no\n";
continue;
}
cout << "yes\n";
D. Sum Graph
分析
发现+n,+(n+1)可以使所有点被连成一条链。
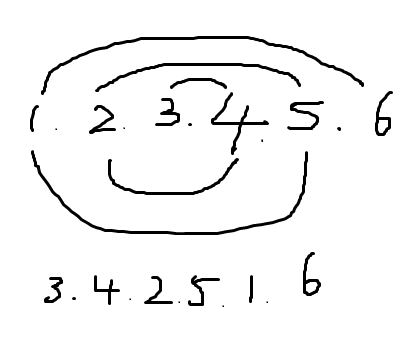
因为本题允许猜两次,所以考虑+(n-2),+(n-1),这样有两个点与其他的点不连通。判断出其他所有点在p中的对应,只剩这两个点不知道,那么猜两次一定有对的。
如果这个思路可行,那也可以把整个图平分成两半,分别处理。可惜这一划分基于可以猜两次,所以不能形成分治的树形结构。
要想区分出其他所有点,那么在建好的图上,每个点在与其他点的最短路的意义下应该是独一无二的。上文形成的链有对称性,无法区分2和5,4和1,3和6,所以还不够。
我又试着+(n-3),+(n-4)等,一无所获。
而且,要取得足以区分出所有点的信息量,按照与其他所有点的最短路的想法,需要超出2n的询问。
在这里,思路停滞了。
交互 - AC(补)
上文的分析中,默认了所有点的答案要同时求出,忽视了本题是一道交互题,可以利用易求的点求出其他点。
同时,上文让两个点不连通的思路只使n减小很小的常数,并没有改变问题的实质,没有充分利用“猜两次”这一出题人刻意为之的问题性质。
基于上面的链,随便取一个点,离他最远的点一定是链的一个端点。 然而无法判断它是哪一个端点。没关系,链有两个端点,猜两次即可。
在与一个给定端点的距离的意义下,每个点都是独一无二的。此时只需一次查询,便可确定一个点的位置。
总询问数2n。
cin >> n;
for (int i = 1, j = n, k = 1; i <= j; ++i, --j) {
b[k++] = j, b[k++] = i;
}
cout << "+ " << n << "\n"; cout.flush();
cin >> flag; if (flag == -2) return 0;
cout << "+ " << n + 1 << "\n"; cout.flush();
cin >> flag; if (flag == -2) return 0;
int pos = 1; a[1] = 0;
for (int i = 2; i <= n; ++i) {
cout << "? " << 1 << ' ' << i << "\n"; cout.flush();
cin >> a[i]; if (a[i] == -2) return 0;
if (a[i] > a[pos]) pos = i;
}
for (int i = 1; i <= n; ++i) {
if (i != pos) {//这里进行了一次与上面重复的查询,无妨,不需那么细致
cout << "? " << pos << ' ' << i << "\n"; cout.flush();
cin >> flag; if (flag == -2) return 0;
a[i] = flag + 1;
}
} a[pos] = 1;
cout << "! ";
for (int i = 1; i <= n; ++i) {
cout << b[a[i]] << ' ';
}
for (int i = 1; i <= n; ++i) {
cout << b[n - a[i] + 1];
if (i < n) cout << ' ';
} cout << "\n"; cout.flush();
cin >> flag; if (flag == -2) return 0;
E. Between
bfs、贪心 - AC(赛后)
123123123…这可以满足所有“a包夹b”条件。但1只有一个,这使要包夹1的数也是有限的,再推下去……理想地,形成一个树形结构,点的深度就是其最多数目。
让(a,b)作为有向图的边构图。
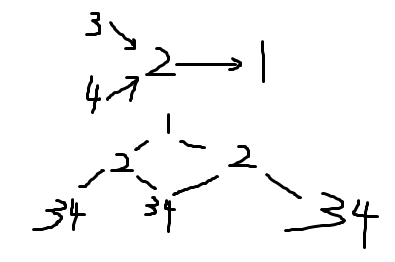
贪心地,让每个数的数目分别最大。
实际上,这个图并不一定那么简单。比如有条件(5,4),(4,3),(3,2),(2,1),和(3,5). 5被3包夹,对5的数目有什么影响?
这里我一开始想错了。(a,b)指的是a中间一定有b,而不是b一定被a包夹。所以从1开始推,一个数的数目只能受到数目已确定的数的影响,b不受a影响。3要夹5,但与链状的情况相同,5的最大数目仍是5.
如果有(5,4),(4,3),(3,2),(2,1),和(5,3),那么1个1,2个2,3个3,4个4,5受到3和4的约束,3的约束更大,所以5有4个。而(5,4)作为同层间包夹,与开篇"123123123"的例子类似,不是问题。
已经可以看出,要求解每个数的最大个数,就是从1开始bfs,实现 下层对上层包夹 约束,层数即是个数。
已经解决了最大长度,还要构造具体序列。上层对下层的包夹 就起了作用。
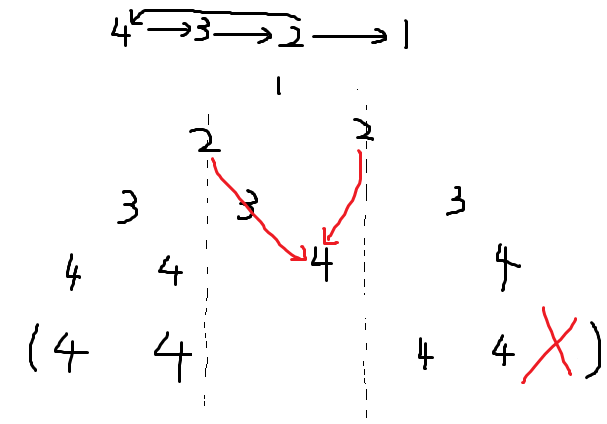
依靠下面这一张图,从左下角扩展,在满足下层对上层包夹的前提下优先走到上层的点,我找到了满足所有上层包夹下层的构造方法:4321 432 43 4.
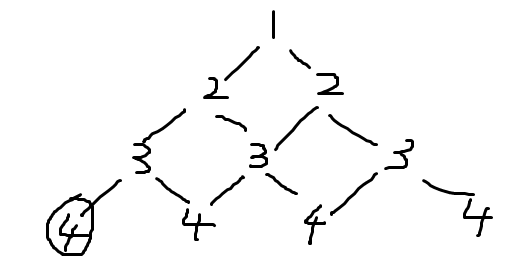
void bfs(int beg) {
memset(d, 0x3f, sizeof(d)); d[1] = 1;
queue<int> q; q.push(1);
while (!q.empty()) {
int u = q.front(); q.pop();
for (int v : g[u]) {
if (ckmin(d[v], d[u] + 1)) {
q.push(v);
}
}
}
}
int main() {
setIO("");
cin >> tt;
while (tt--) {
ans = md = 0;
flag = false;
cin >> n >> m;
for (int i = 1; i <= n; ++i) {
vector<int>().swap(g[i]);
vector<int>().swap(num[i]);
}
for (int i = 1; i <= m; ++i) {
int u, v; cin >> u >> v;
g[v].push_back(u);
}
bfs(1);
for (int i = 1; i <= n; ++i) {
if (d[i] >= INF) {
flag = true;
break;
}
ans += d[i];
num[d[i]].push_back(i);
ckmax(md, d[i]);
}
if (flag) {
cout << "INFINITE\n";
}
else {
cout << "FINITE\n";
cout << ans << "\n";
for (int i = 1; i <= md; ++i) {
for (int j = md; j >= i; --j) {
for (int k : num[j]) {
cout << k << ' ';
}
}
} cout << "\n";
}
}
return 0;
}
D. XOR Counting
状压dp - TLE 无代码(赛后)
分别考虑每一位的异或结果。考虑第i位。
加、异或都有交换律。
要让m个数和为n。和的第i位受到m个数的自第i位及更低位的影响,而不会受到更高位的影响。所以从低向高考虑这m个数各位上的数码,每个位上可以加0~m个1并进位(和与n吻合,所以个数受到奇偶性限制),从而影响更高位,且不再影响更低位。
这让人想到[NOIP2021] 数列。定义状态
(
i
,
j
)
(i,j)
(i,j)表示处理到第i位,舍弃i的更低位后剩余的进位的数是j。i的更低位不会再改变,也与后面的问题无关,无需记录在状态中。易知j最大约为
l
o
g
m
logm
logm.
转移时,需要枚举m个数中第i位是1的数的个数。
时间复杂度
O
(
T
×
60
m
l
o
g
m
)
O(T\times 60mlogm)
O(T×60mlogm),超时。
算法瓶颈在于m,即转移时枚举加1的个数。
结论、dp - AC(补)
当m=1时,答案显然是n.
当m大于等于3时,对于与n奇偶性相同且不超过n的数x,因为 a ⊕ b ⊕ b = a \boldsymbol{a\oplus b\oplus b=a} a⊕b⊕b=a,构造 ( x , ( n − x ) / 2 , ( n − x ) / 2 , 0 , ⋯ ) \boldsymbol{(x,(n-x)/2, (n-x)/2, 0,\cdots)} (x,(n−x)/2,(n−x)/2,0,⋯)使x加入答案统计。因为 a ⊕ b \boldsymbol{a\oplus b} a⊕b与 a + b a+b a+b同奇同偶且 a ⊕ b ≤ a + b \boldsymbol{a\oplus b\leq a + b} a⊕b≤a+b,所以上述构造可以包含所有可能的异或结果。
当m=2时,上文的状压dp不会超时。
j只能是0或1,我选择从高向低,记搜。
别忘取模。
int tt;
ll n, m, dp[62][2], cnt[62][2];
ll powmod(ll a, ll b, ll p) {
if (!b) return 1;
if (b & 1) return powmod(a, b - 1, p) * a % p;
ll t = powmod(a, b >> 1, p); return t * t % p;
}
void f(int i, int j) {
if (!i) return;
if (cnt[i][j] != -1) return;
if (j) {
if (n >> i - 1 & 1) {
f(i - 1, 1);
cnt[i][j] = cnt[i - 1][1];
dp[i][j] = dp[i - 1][1];
}
else {
f(i - 1, 0); f(i - 1, 1);
cnt[i][j] = (cnt[i - 1][0] + cnt[i - 1][1]) % MOD;
dp[i][j] = (dp[i - 1][0] + dp[i - 1][1]) % MOD;
}
}
else {
if (n >> i - 1 & 1) {
f(i - 1, 0); f(i - 1, 1);
cnt[i][j] = (cnt[i - 1][0] + cnt[i - 1][1]) % MOD;
dp[i][j] = (dp[i - 1][0] + dp[i - 1][1]) % MOD;
}
else {
f(i - 1, 0);
cnt[i][j] = cnt[i - 1][0];
dp[i][j] = dp[i - 1][0];
}
}
if (j ^ n >> i & 1) plusmod(dp[i][j], cnt[i][j] * powmod(2, i, MOD));//直接位运算可能爆longlong
}
int main() {
setIO("");
cin >> tt;
while (tt--) {
cin >> n >> m;
memset(cnt, -1, sizeof(cnt));
cnt[0][0] = 1; dp[0][0] = n & 1;
cnt[0][1] = 0; dp[0][1] = 0;
if (m == 1) {
cout << n % MOD << "\n";
}
else if (m == 2) {
f(60, 0);
cout << dp[60][0] << "\n";
}
else if (n & 1) {
cout << ((n + 1) / 2 % MOD) * ((n + 1) / 2 % MOD) % MOD << "\n";
}
else {
cout << (n / 2 % MOD) * ((n + 2) / 2 % MOD) % MOD << "\n";
}
}
return 0;
}