【写在前面】也是趁着五一假期前再写几篇分享类的文章给大家，希望看到我文章能给软考网络管理员备考的您带来一些帮助，5月27号也是全国计算机软件考试统一时间，也就不用去各个地方找资料和代码了。紧接着我就把我整理的一些资料分享给大家哈，主要针对全国软考网络管理员初级资料之数据通信技术
常考知识点：奇偶校验概念，海明码校验概念，CRC校验，常见编码技术（曼彻斯特编码和差分曼彻斯特编码，4B5B 编码，8B6T）及其应用场景，什么是奈奎斯特定理，什么是香农定理。

1、信道技术

1.1奈奎斯特定理

奈奎斯特推导出在理想信道（无噪声寸扰）的情况下最高码元的传输速率的公式：B=2W, 传输速度超过此上限，就会出现严重的码间串扰问题，使得接收端对码元的识别成为不 可能。波特是 码元传输的速率单位，它说明每秒传送多少个码元。码元的传输速率也称 为调制速率、波形速 率，反映信号波形变换的频繁程度。 比特是信号量的单位，信息的传输速率 bps 和波特率在数量上有一定的关系。如果一个 码元（取 2 个离散值）只携带 1 比特的信息量，贝 U 两者之间的数值相等。如果一个码元（取 4 个离散值）， 则代表携带 2 比特的信息量。 具体的换算公式为：R=Blog2N （R 为比特率 bps、B 为波特率，N 为码元种类）。

1.2香农定理

香农用信息论的理论推导出了带宽受限且有噪声干扰的信道的极限信息传输速率 R=Wlog2 （1+S/N）。在使用香农理论时由于 S/N（信噪比）的比值通常太大，因此通常 使用分贝数（dB） 来表示，即 XdB=101ogio （S/N）o 要注意的是，奈奎斯特定理和香农定理两种算法得出的结论不能够直接比较，因为其假 设条 件不同。在香农理论中实际也考虑了调制技术的影响，但由于高效的调制技术往往 会使出错 的可能性更大，因此也会有一个极限，故香农理论的计算方式忽略采用调制技术。

1.3信道复用技术

多路复用技术把多个低速信道组合成一个高速信道的技术,可以有效地提高数据链路的 利用 率。 多路复用的原理如图 2-1 所示。

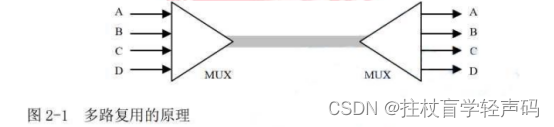
1.多路复用分类 信道多路复用技术按照实现的方式和原理可以分为空分复用、频分复用、时分复用、波 分复 用以及码分复用。表 2-1 所示为多路复用技术的特性与应用。
表 2-1 复用技术的特性与应用

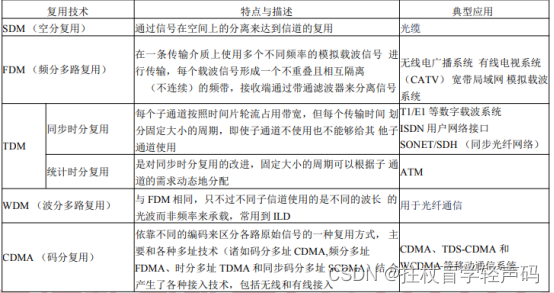
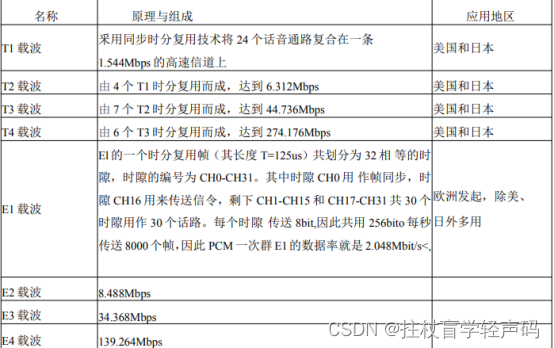
2.数字传输系统复用标准 早期通信中使用的时分多路复用传输系统主要有准同步数字系列（PDH） , PDH 数字 传输系 统的原理、组成与应用地区如表 2-2 所示。 表 2-2 常见的数字传输系统的原理、组成与应用地

2、信号技术

2.1 调制技术

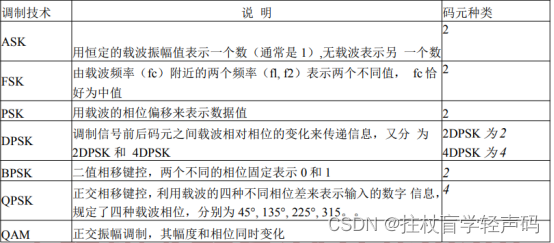
所谓调制就是进行波形变换。更严格讲，就是进行频谱变换，将基带数日信号的频谱变 换为 适合在模拟信道中传输的频谱。 最基本的调制技术包括幅移键控（ASK）、频移键控（FSK）和相移键控（PSK）等几 种。其特性如下表所示：

2.2 PCM 技术

模拟数据必须转变为数字信号，才能在数字信道上传送，这个过程称为“脉冲编码调制 PCM 技术” 。PCM

2.3 编码技术

在用数字信道中传输计算机数据时，要对计算机中的数字信号重新编码进行基带传输。 二进 制数字信息在传输过程中可采用不同的代码，这些编码的抗噪性和定时能力各不相同。 1.基本编码 基本的编码方法有极性编码如图 2-2 所示

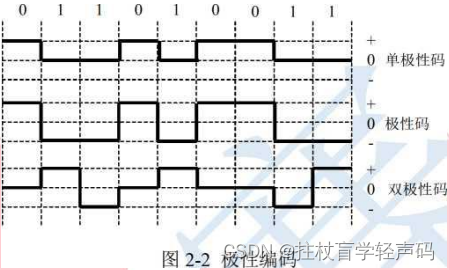
（1）极性编码（如图 2-2 所示）：极性包括正极和负极两种，单极性码只使用一个极 性， 再加零电平（正极表示 0,零电平表示 1）的编码；极性码使用了两极（正极表示 0, 负极表示 1）的 编码；双极性码则使用了正负两极和零电平（其中有一种典型的双极性码是 信号交替反转编码 AML 它用零电平表示 0, 1 则使电平在正、负极间交替翻转）的编码。 在极性编码方案中始终使用某一特定的电平来表示特定的数，因此当连续发送多个 1 或 0 时， 将无法直接从信号判断出个数。要解决这个问题就需要引入时钟信号。
（2）归零性编码 归零码就是指码元中间的信号回归到零电平。不归零码则不回归零（而是当 1 时电平翻 转，0 时不翻转），这也称之为差分机制。值得注意的是这里讲的不归零码实际是不归零反 转码，还有 一种就是常规的不归零码，就是用高电平表示 1,低电平表示 0。
（3）双相码 通过不同方向的电平翻转（低到高代表 0,高到低代表 1）,这样不仅可以提高抗干扰 性，还可 以实现自同步，它也是曼彻斯特编码的基础。 吨畚屯 m 屯 f 打扫巨主比 Z 码 t I I I I I I I ti 0 110 10 0 11 2.应用性编码 应用性编码主要有曼彻斯特编码、差分曼彻斯特编码、4B/5B 编码、8B/6T 编码和 8B/10B 编码 等。 （1）曼彻斯特编码和差分曼彻斯特编码 曼彻斯特编码和差分曼彻斯特编码如下图所示。

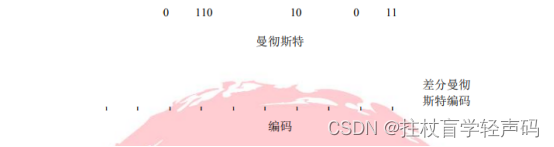
曼彻斯特编码是一种双相码，在曼彻斯特编码中，每一位的中间有一跳变，位于中间的 跳 变既作时钟信号，又作数据信号；从高到低跳变表示“0”，从低到高跳变表示“1”。（注 意：某些 教程中关于此部分内容有相反的描述，即从高到低跳变表示“1”，从低到高跳变 表示“0”，也是正 确的），因此它也可以实现自同步，常用于以太网（IEEE 802.3 10M 以 太网）。 差分曼彻斯特编码在每个时钟周期的中间都有一次电平跳变,这个跳变做同步之用。在 每个 时钟周期的起始处：跳变则说明该比特是 0,不跳变则说明该比特是 1。这里有个技巧 记忆，主要 看两个相邻的波形，如果后一个波形和前一个的波形相同，则后一个波形表示 0, 如果波形不同， 则表护 1。常用于令牌环网。 注意：曼彻斯特编码作为一种数字信号的编码是一个码元对应昴高电平或者一个低电 平的。 而曼彻斯特编码是用相邻两个电平来表示一 bit,使用曼码和差分曼码时，每传输 Ibit 的信息，就 要求线路上有 2 次电平状态变化，所以这两种编码方式的效率只有 50%。
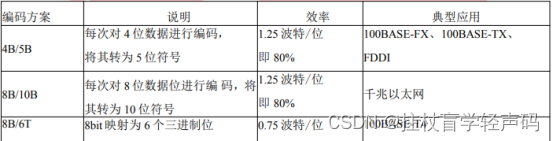
（2）4B/5B 编码、8B/6T 编码和 8B/10B 编码 正是因为曼码的编码效率不高，鬲此在带宽资源宝贵的广域网，以及速度要求更高的局 域 网中，就面临困难。因此就出现了 mBnB 编码，也就是将 m 比特位编码成为 n 波特（代 码位）。 4B/5B 编码、8B/6T 编码和 8B/10B 编码的比较如下图所示。

3、差错控制

3.1 奇偶校验

奇偶校验码是最简单的检错码，由于实现起来比较容易而被广泛采用。这种码的校验关 系 可以用一个简单的方程来表示。设要传送用户比特信息为 C1C2C3C4C5,其中校验码 Ci 取值“0” 或“1”。 经过编码以后变成六比特编码码字，其中校验位 C6 应满足下列关系： Cl + C2 + C3 + C4 + C5 + C6 = 0 （或 1） 算式中的加法是模 2 加。上式的右边等于零称为偶校验，此时等式的右边含偶数个 1； 等于 1 就是奇校验，则含奇数个 lo 在接收端，将收到 Cl, C2, C6 比特进行累加，检查其是否符合式的关系。如果收 到的码组符合奇偶校验关系，则认为传输没有错。实际上，它是可能错的。因为，如果偶数 位 发生错误，则接收端根据奇偶校验关系仍然认为没有错误。奇偶校验码可以发现所有奇数个错误。

3.2 海明校验

海明校验是在数据中间加入几个校验码，码距均匀拉大，将数据的每个二进制位分配在几个奇偶校验组里，当某一位出错，会引起几个校验位的值发生变化。 海明校验码个数为 K, 2 的 K 次方种校验信息，1 个校验信息用来指出“没有错误”， 其余 2 匕 1 个指出错误发生在哪一位，所以满足 E 奸 1W2A 对于海明码校验位存放位置：一般情况海明码是放置在二的冨次位上的，即 “1,2,4,8,16…” o 例如：
例如：以信息码101101100,并采用偶校验

海明码的监督关系式有：

Bl®B3®B5®B7®B9®BllffiB13=0 
B2®B3®B6®B7®B10®Bll=0 
B4®B5®B6®B7®B12®B13=0 
B8®B9®B1O®B11®B12®B13=O 

由监督式可以看出，信息位 B3 受校验位 Bl、B2 的监督，信息位 B5 受校验位 Bl、B4 的监督，信息位 B6 受校验位 B2、B4 的监督，信息位 B7 受校验位 Bl、B2、B4 的监督， 依此类推， 假设有 14 位，那么第 14 位应该受 B2、B4、B8 校验位监督。所以可以算出 B1、 B2、B4、B8 的 值。 然后将结果填入，得到我们经过差错编码的数据串如图 2-8 所示：

如果给出一个加入了校验码的信息，并说明有一位错误，则可以采用基本相同的方法找 出 这个错误的位。 例如监督关系式目前为：

Bl©B3©B5©B7©B9©Bl 1©B13 = 1©1©0©1©0©0©0 =1 
B2©B3©B6©B7©BIO©Bl 1 = 1©1©1©1©1©0 =1 
B4©B5©B6©B7©B12©B13 = 0©0© 1©1 ©0©0=0 
B8©B9©B1O©B11©B12SB13 =0©0©1©0©0©0=1 

我们可以判断出只有 B11 出错，才会导致第一个、第二个、第四个监督关系式出错， 我们 只需要把第 11位恢复即可。

3.3 CRC 校验

海明校验过于复杂，而 CRC 的实现原理十分易于用硬件实现，因此广泛地应用于计算 机网 络上的差错控制。 计算 CRC 校验码基于 CRC 生成多项式，如原始报文为 11001010101,其生成多项式为 x 4+x 3+x+lo 计算时在原始报文的后面添加若干个 0（等于校验码的位数，而生成多项式的 最高幕 次就是校验位的位数，本题中使用该生成多项式产生的校验码为 4 位）作为被除数, 除以生成多 项式所对应的二进制数（根据其幕次的值决定，得到 11011,因为生成多项式中 除了没有 x2 之外， 其他位都有）。使用模 2 除，得到的商就是校验码。然后将 0011 添加到 原始报文的后面就是结 果，即 110010101010011c 将 0011 添加到原始报文的后面就是结果 110010101010011c 如图 2.9 所示。 检查信息码是否出现了 CRC 错误的计算很简单，只需用待检查的信息码做被除数，除 以生 成多项式。如果能够整除说明没有错误；否则出错。另外要注意当 CRC 检查出现错误 时，它不 会纠错，通常是让信息的发送方重发一遍；

4.片尾彩蛋

倾心打造佳作，愿解君之惑，如若有幸，盼君上榜助阵，特此敬谢！
皇榜入口点击此处