2023-04-29 动态规划介绍

动态规划是运筹学课程的一部分

多阶段决策问题

有一类活动的过程，可以分成若干个互相联系的阶段，在它的每一阶段都需要作出决策，从而使整个过程达到最好的活动效果

当然，每个阶段的决策的选取不是任意确定的，它依赖于当前的状态，又会影响以后的发展

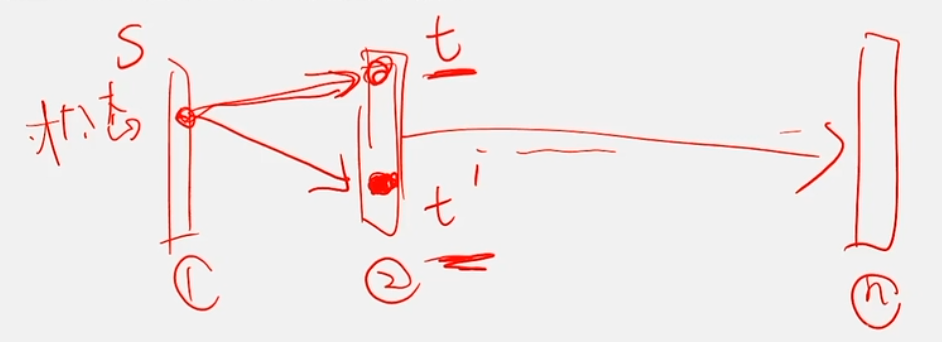
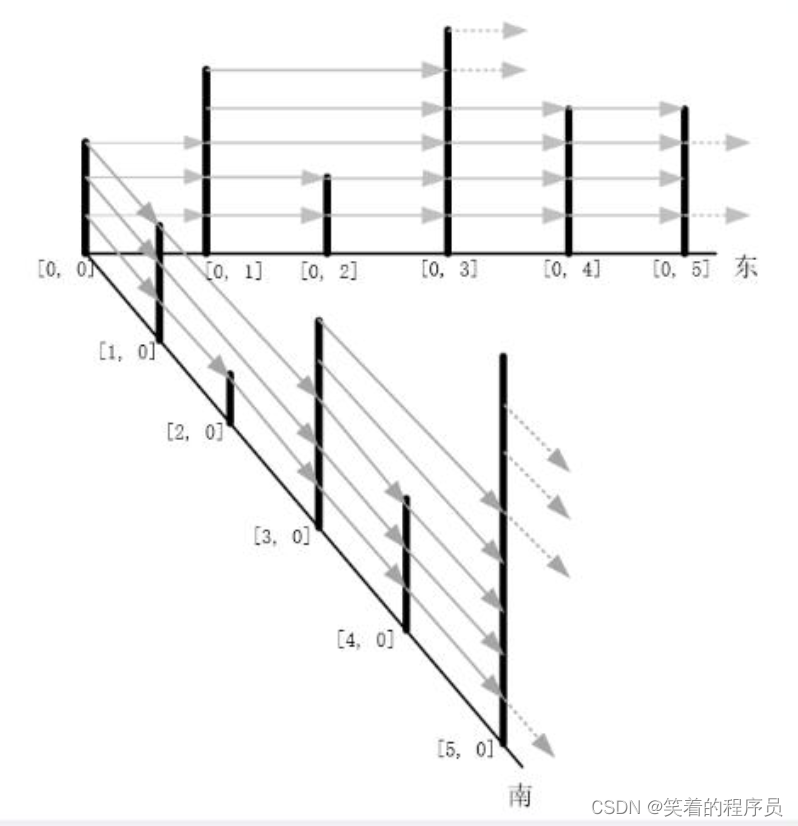
如下图，①、②...n这些长条代表整体过程按指定条件划分的阶段，$s、t、t_1$代表阶段中对象的状态，$s-->t$或$s-->t_1$的箭头线代表阶段的转移即决策，可以看出一个阶段到下一个阶段的决策是可能有多种的，所以称为多阶段决策问题

当各个阶段决策决定以后，就组成一个决策序列，因而也就确定了整个过程的一个活动路线。

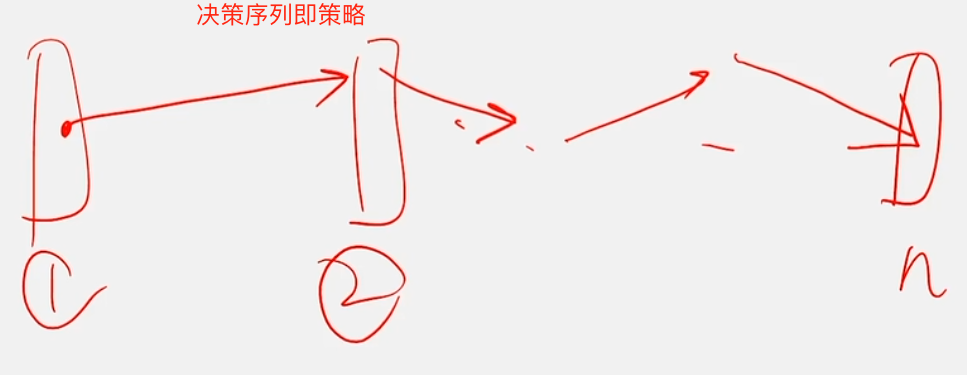
这种把一个问题看做事一个前后关联、具有链状结构的多阶段过程就称为多阶段决策过程，这种问题就称为多阶段决策问题

动态规划问题

寻找上述多阶段决策过程中最优策略(即最优链路)的过程就是动态规划

各个阶段采取的决策，一般来说是与阶段有关的。

决策依赖于当前的状态，又随即引起状态的转移。

一个决策序列就是在变化的状态中产生出来的。

称这种解决多阶段决策最优化的过程为动态规划(Dynamic Programming，即DP)

动态规划是对解最优化问题的一种途径、一种方法，而不是一种特殊方法

由于各种问题的性质不同，确定最优解的条件也各不相同，因此不存在一种万能的动态规划算法可以解决各类最优化问题

在学习动态规划问题时，除了要对基本概念和方法正确理解之外，还必须要对具体问题具体分析，以丰富的想象力去建立模型，用创造性的技巧去求解

我们将通过对若干有代表性的问题的动态规划算法进行分析、讨论，逐渐学会并掌握这一设计方法

进一步地，还会介绍一些常见的优化动态规划的时空复杂度的做法，从而冲刺高分，希望他同学们最好能够掌握

常见的DP问题类型

参考博客：基本DP模型总结

• 线性DP：在一个序列上划分n个阶段求最佳策略
• 区间DP：以区间为状态，即$f[l][r]$表示区间$[l,r]$的答案.
• 背包DP：固定体积的背包，如何装不同价值的物品来达到价值最大
• 数位DP：统计满足一定条件的数的数量

  数位：把一个数字按照个、十、百、千等等一位一位地拆开，关注它每一位上的数字。如果拆的是十进制数，那么每一位数字都是 0~9，其他进制可类比十进制。

• 状态压缩DP：记录DP中简单状态(能用0和1表示)，一个最简单的方法是记录n个0/1，但这样子太麻烦了，可以把这n个0/1压成一个数，进而利用计算机中方便的二进制操作进行转移.
• 树状DP：简单的树形DP通常是设f[i]表示以i为根的子树，然后直接把所有儿子合并到父亲身上.

常见的DP优化方法

• 节省时间的优化方法
  • 矩阵乘法优化
  • 斜率优化
  • 四边形不等式优化
  • 决策单调性优化
• 节省空间的优化方法
  • 滚动数组优化

    滚动数组实际就是滑动窗口

• 同时优化时间和空间的方法
  • 数据结构优化