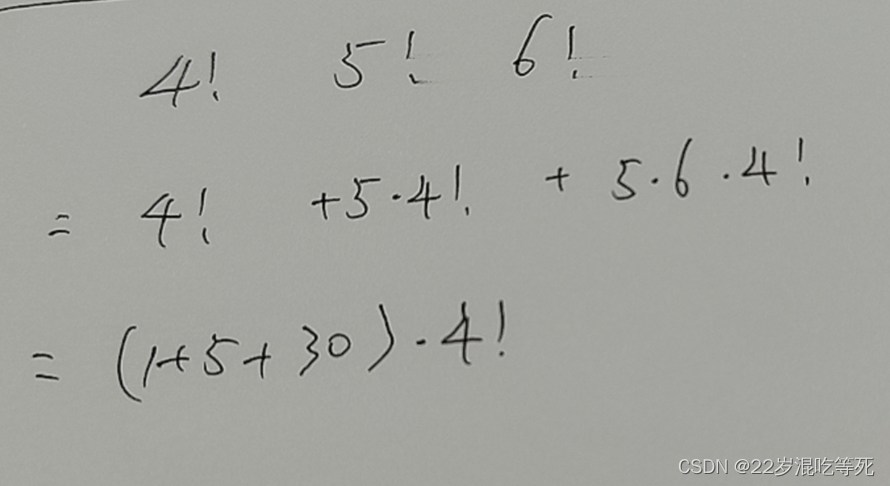数据科学基础数学:线性代数简介 了解标量、向量和点积
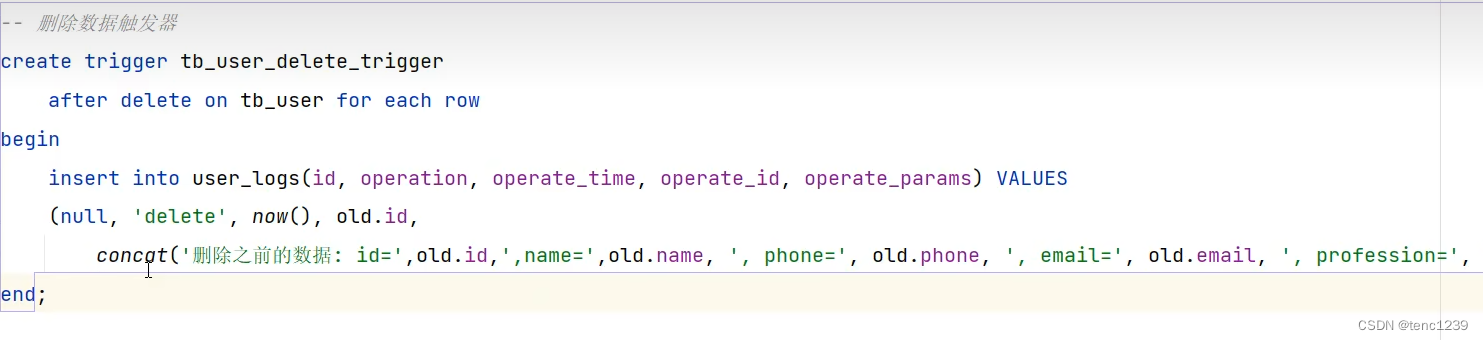
机器只能按着算法理解和处理数据结构存储的数字.
例如创建垃圾邮件检测器,则首先必须将文本数据转换为数字(通过单词嵌入)。
两个句子之间的余弦相似性 两个句子之间的余弦相似性可以通过它们的向量表示法的点积来找到。有多种方法可以将句子/段落表示为向量。
similarity
= cos(a,b)
= dotproduct(a,b) / ( norm(a) * norm(b) )
= a.b / ||a|| * ||b||
这里有两个非常短的文本可以比较:
Julie loves me more than Linda loves me
Jane likes me more than Julie loves me
我们想知道这些文本的相似程度,纯粹从字数上看(而忽略了字数顺序)。我们首先列出两篇文章中的单词:
me Julie loves Linda than more likes Jane
现在我们计算这些词在每个文本中出现的次数:
me 2 2
Jane 0 1
Julie 1 1
Linda 1 0
likes 0 1
loves 2 1
more 1 1
than 1 1
对这两个垂直向量的计数感兴趣。例如,每个文本中都有两个 "我 "的例子。我们将通过计算这两个向量的一个函数,即它们之间的角度的余弦,来决定这两个文本之间的距离。
这两个向量也是如此:
a: [2, 1, 0, 2, 0, 1, 1, 1]
b: [2, 1, 1, 1, 1, 0, 1, 1]
它们之间的角度的余弦约为0.822。
这些向量是8维的。使用余弦相似性的一个优点显然是,它将问题转化为可视化。在这种情况下,你可以把它看作是大约35度的角度,这与零或完全一致有一些 "距离"。
在我们的下一篇文章中,我们将看到实时的实现。
然后可以将数据存储在向量、矩阵和张量中。图色彩表示为 0 到 255 之间的值矩阵,表示每个像素的每种颜色的亮度。可以利用线性代数领域的工具和概念来操作这些向量、矩阵和张量。
问题描述:数学求解不在我讨论的重点,转向使用 python 求 2D 平面空间的3个点所决定的三角形三边之间的角度。
矢量分析中的点积将用于计算3点之间的角度。
我们使用了多个维度数据,如 1D、2D、3D 和更高维度,而不仅仅是 2D。但我用2D数据点解释。
点积,可以用代数或几何方式定义。几何定义基于角度和距离,矢量的大小的概念。这两个定义的等价性依赖于欧几里得空间的笛卡尔坐标系。
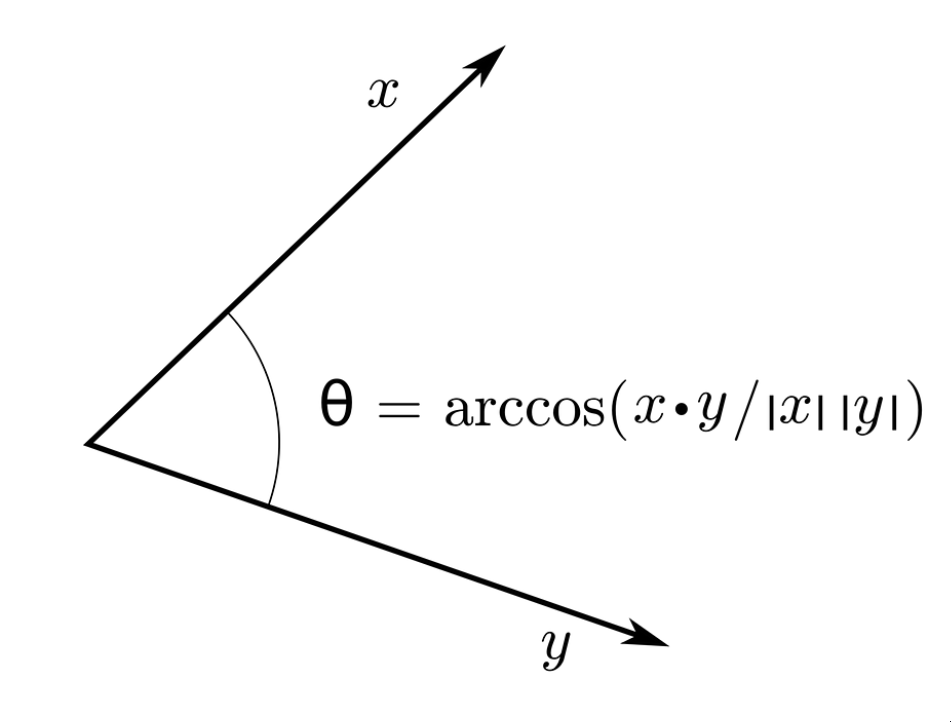
几何定义:
同时具有大小和方向的几何对象。矢量可以描绘成箭头,大小是它的长度,它的方向是箭头指向的方向。
向量 a 的大小用 a 表示|a|
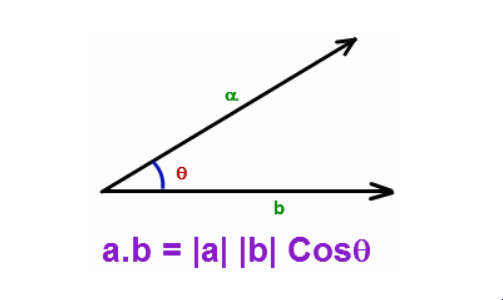
两个欧几里得向量 a 和 b 的点积由下式定义。其中 θ 是 a 和 b 之间的角度。
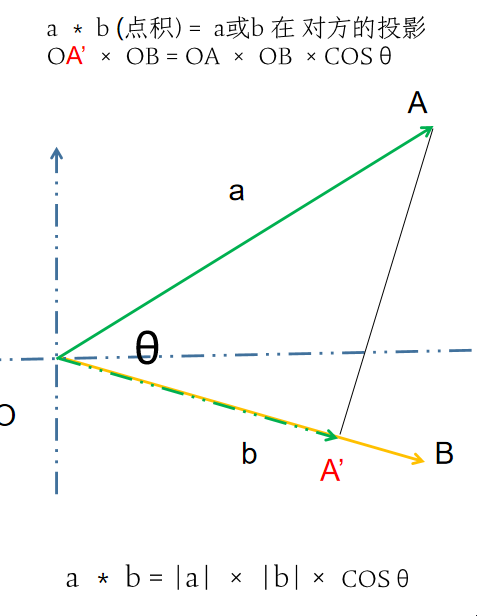
解释:

Linear Algebra
使用Math库的写法不是今天讨论的重点。因为写法1只照顾到我们熟知的数学思路,仅在最后一步调用对应的python函数求解。
换句话话说,写法1人理解起来比较容易,但在机器看来并不是它的菜。
import math
def getAngle(a, b, c):
y_ca,x_ca = c[1] - a[1], c[0] - a[0]
y_ba,x_ba = b[1] - a[1], b[0] - a[0]
ang = math.degrees(math.atan2(y_ca,x_ca) - math.atan2(y_ba,x_ba))
return ang + 360 if ang < 0 else ang
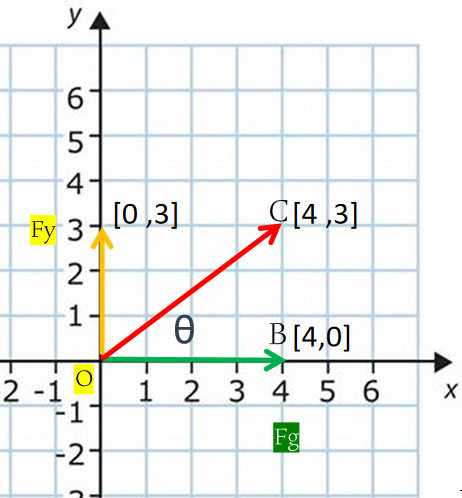
a,b,c = (0,0),(4,0),(4,3)
print(getAngle(a, b, c))
36.86989764584402
今天的重点是在第2种思路:Numpy
a ∗ b (点积) = (a 或 b 在b或a方向上的投影) × (b 或 a)
OA’ × OB = OA × OB ×COSθ
a ∗ b = |a| × |b|× COSθ
numpy.dot() #计算 a ∗ b = 9
numpy.linalg.norm() #|a| × |b|
导入上一篇的任务链接在此👇,继续深入求解斜拉的两根绳索与水平呈的角度是多少?
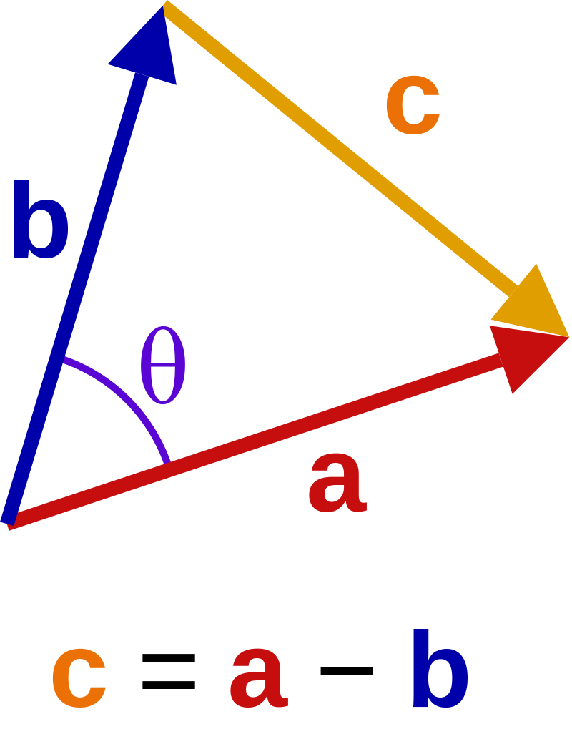
上期课程直观向量相加的概念:
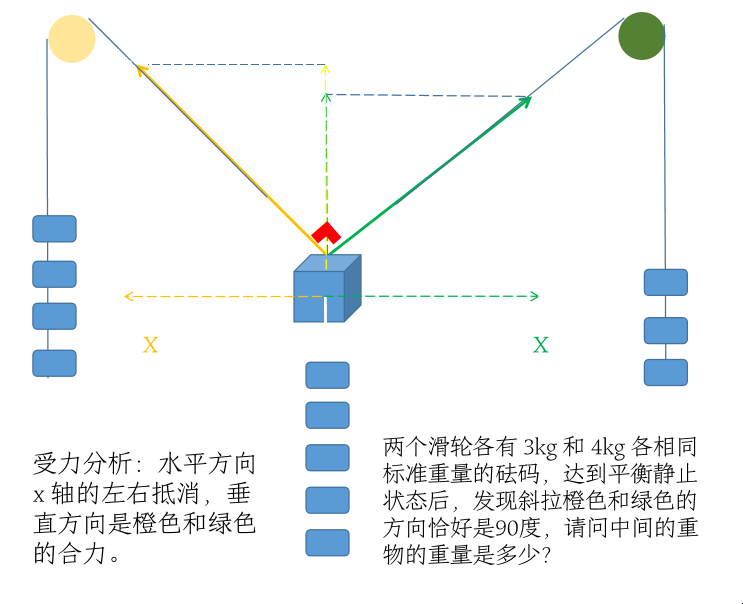
OC = OA + OB #合力
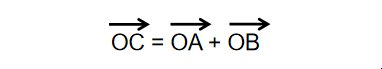
代码解释:
1、点积 运算
numpy求点积:np.dot的函数
2、范式 运算
numpy求范数:np.linalg.norm

图示的过程代码实现如下:
import numpy as np
# c a = angle
#a,b,c = (0,0,0),(1,0,1),(1,1,1)
a,b,c = list(map(list,(a,b,c)))
a = np.array(a)
b = np.array(b)
c = np.array(c)
# O
ba = b - a
ca = c - a
print(ba,ca) #[ 0 -3] [ 4 -3]
cosine_angle = np.dot(ba, ca) / (np.linalg.norm(ba) * np.linalg.norm(ca))
angle = np.arccos(cosine_angle)
#a,b,c = (0,0),(0,3),(4,0)
print('c与b 的夹角',np.degrees(angle))
c与b 的夹角 36.86989764584401
如何推而广之?
在四面体分子的几何结构中,一个中心原子位于中心位置,四个取代基位于四面体的四角。当所有四个取代基都相同时:
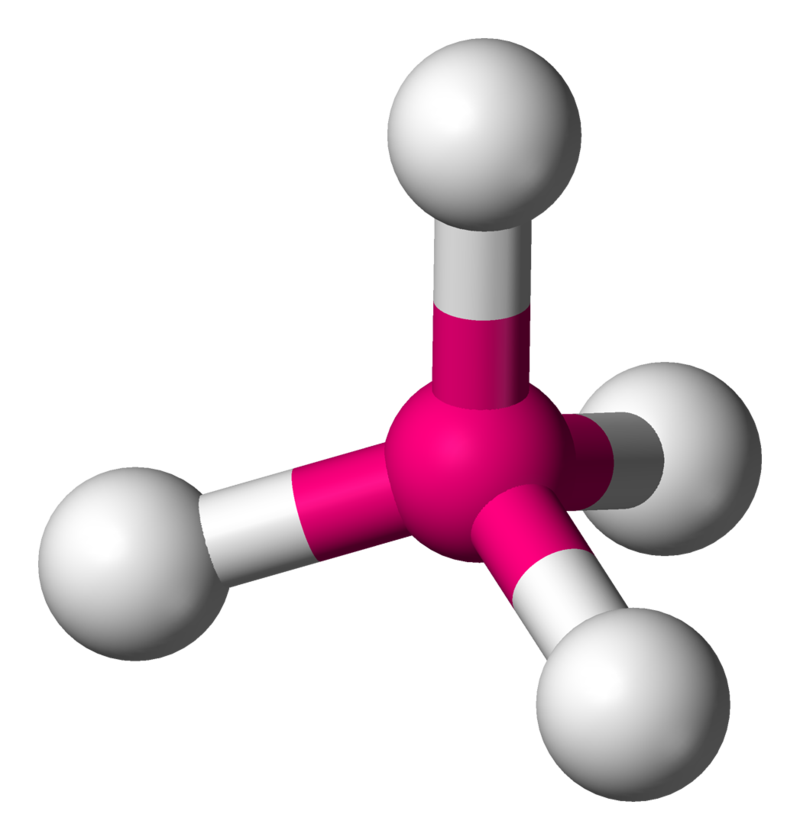
四面体的键角
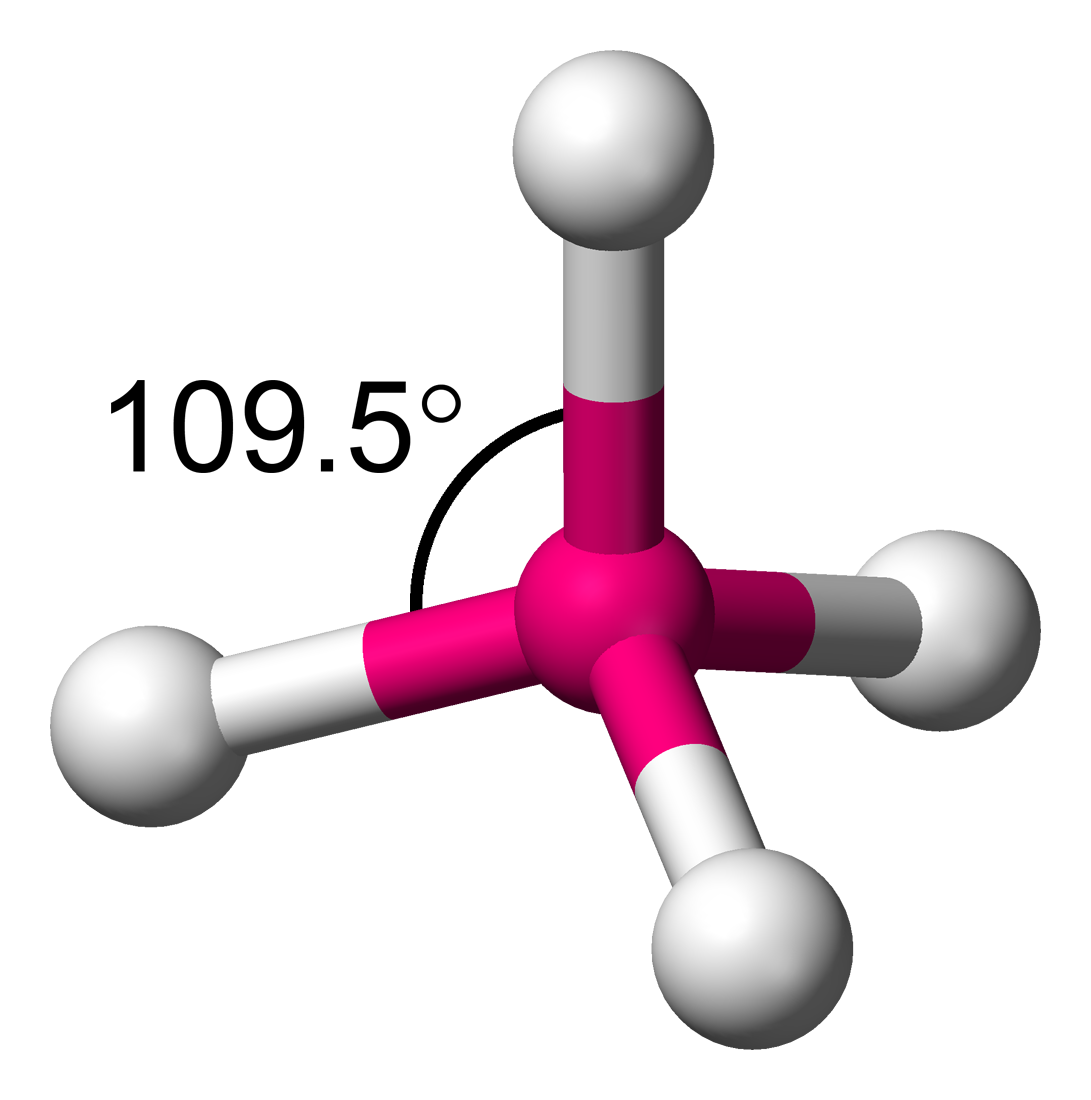
cos-1(-1⁄3)=109.4712206°≈109.5°
如甲烷CH4以及其较重的类似物。甲烷和其他完全对称的四面体分子属于点群Td,但大多数四面体分子的对称性较低。
四面体的键角用点乘法计算对称四面体分子的键角。 对称的四面体分子如CH4的键角可以用两个向量的点积来计算。
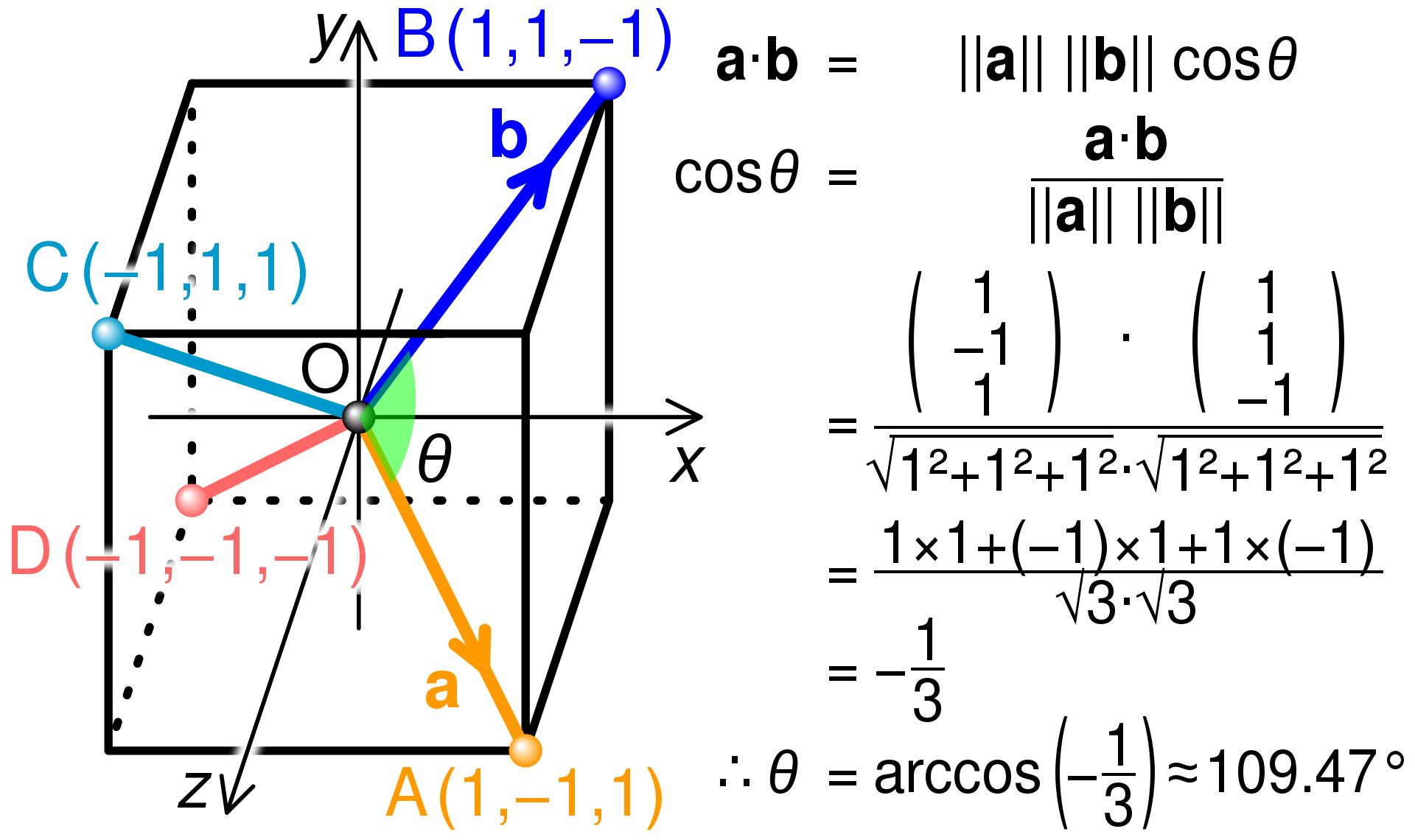
如图所示,分子可以被刻在一个立方体中,四价原子如碳位于立方体中心,也就是坐标的原点O。
四个单价原子,如氢位于立方体的四个角A、B、C、D,选择这些角时,没有两个原子位于相邻的角,
只由一条立方体边连接。如果立方体的边长选择为2个单位,那么两个键OA和OB对应于矢量:
a = (1,-1,1)和
b = (1,1,-1),而键角θ是这两个矢量之间的角度。
这个角度可以通过这两个矢量的点积来计算,定义为
a-b=||a||||b||cos θ
其中|a|表示矢量a的长度。如图所示,这里的点积为-1,每个矢量的长度为√3,所以cos θ=-1/3,四面体的键角θ = arccos(-1/3) ≃ 109.47°
(0,0,0),(1,-1,1),(1,1,-1)
import numpy as np
# c a = angle
a,b,c = (0,0,0),(1,-1,1),(1,1,-1)
a,b,c = list(map(list,(a,b,c)))
a = np.array(a)
b = np.array(b)
c = np.array(c)
# c 与 b 的夹角 b-a , c-a
ba = b - a
ca = c - a
cosine_angle = np.dot(ba, ca) / (np.linalg.norm(ba) * np.linalg.norm(ca))
angle = np.arccos(cosine_angle)
print('np-c与b 的夹角',np.degrees(angle)) #,math.cos()
c与b的夹角 109.47122063449069
立方体键角
第 3 步 数学工具
线性代数中的一个基本运算符。它被称为点积或两个向量的内积。你们中的大多数人已经熟悉这个运算符,实际上它很容易解释。
两个向量之间的点积可以解释为向量 vec{v}上的向量 vec{w}的投影。然后,我们将投影向量 vec{w}的长度乘以vec{v}的长度。
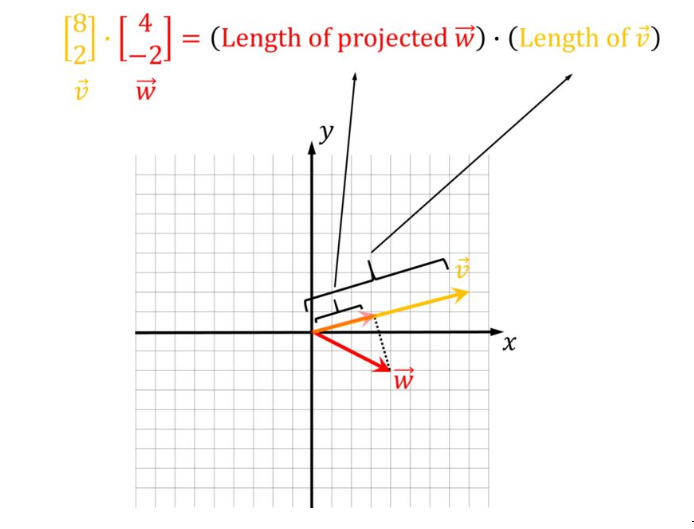
然而,我们将提供一些额外的见解以及如何在 Python 中使用它的一些基本信息。
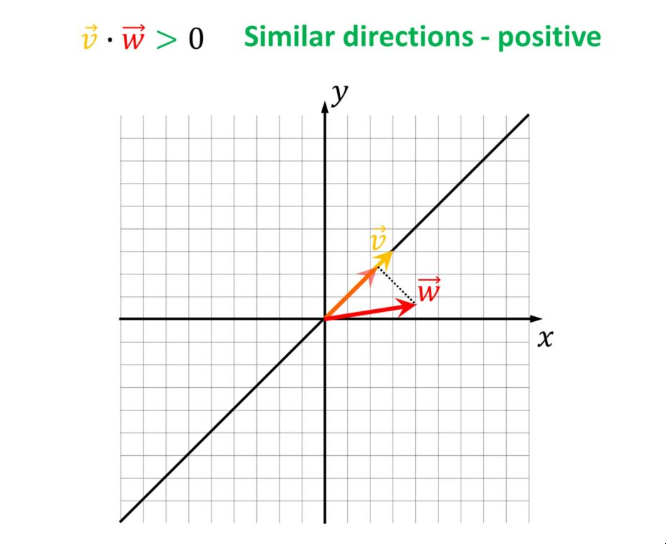
因此,根据两个向量之间的角度,我们可以有以下情况。
例如,如果内积为正,则两个向量之间的角度小于锐角。
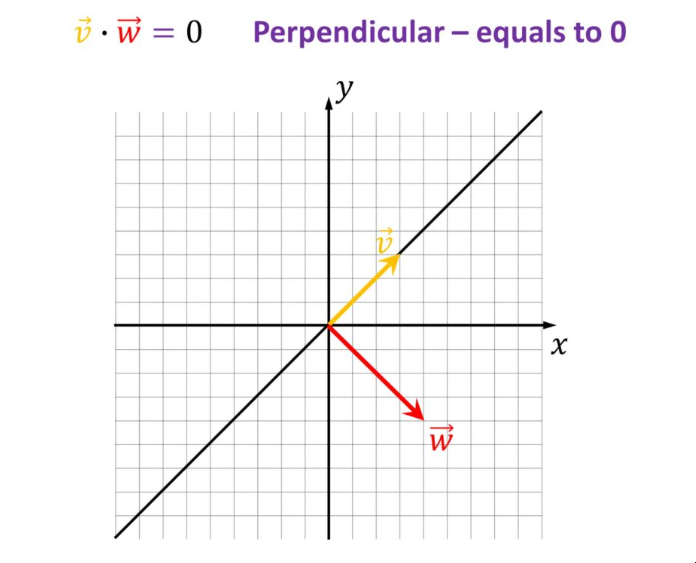
如果向量垂直,则内积为零。这是一个重要的结论!对于这样的向量,我们说它们是正交的。
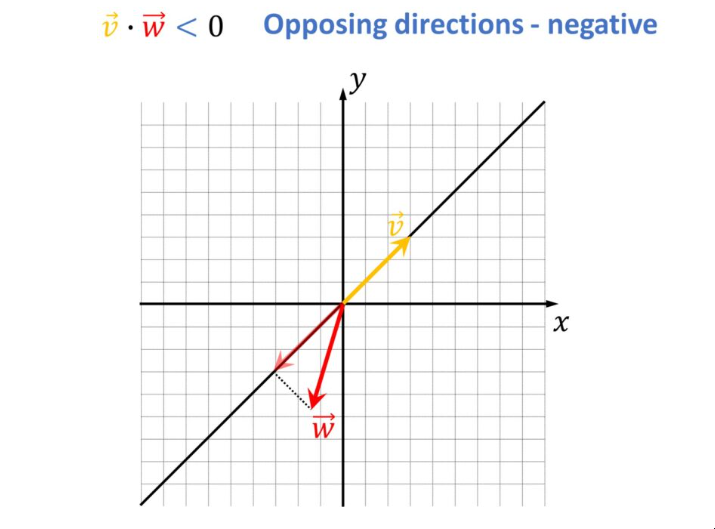
如果向量产生钝角,则内积将为负数。
内积还有一个技巧。内积是一个交换向量运算。基本上,这意味着我们可以在vec{w}上投影vec{v},在这种情况下,我们将有一个投影 vec{v}的长度乘以 vec{w}的长度,因此我们将获得相同的结果。
让我们进一步探讨内积的交换性质。
如果 vec{v} 和 vec{w} 碰巧具有相同的长度,我们可以利用对称性。好吧,我们可以看到 vec{w} 到 vec{v}上的投影长度与投影到 vec{w}上的长度相同。这样,很明显,两种计算方法的内积是相同的。
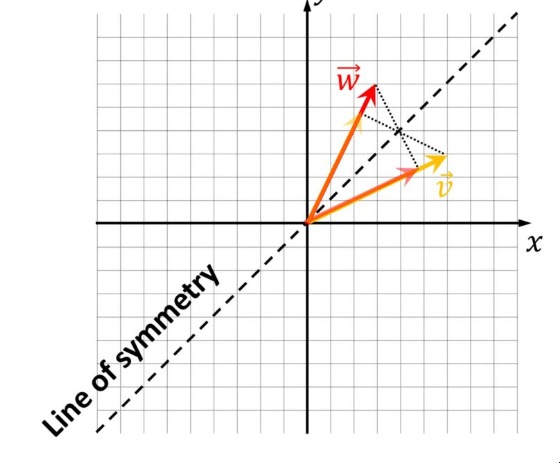
此外,我们可以假设其中一个向量,假设vec{v},比vec{w}长3倍。现在,我们看到我们不能有相同长度的投影。
但是,我们可以将其解释为 3 vec{v}向量的简单缩放vec{v}
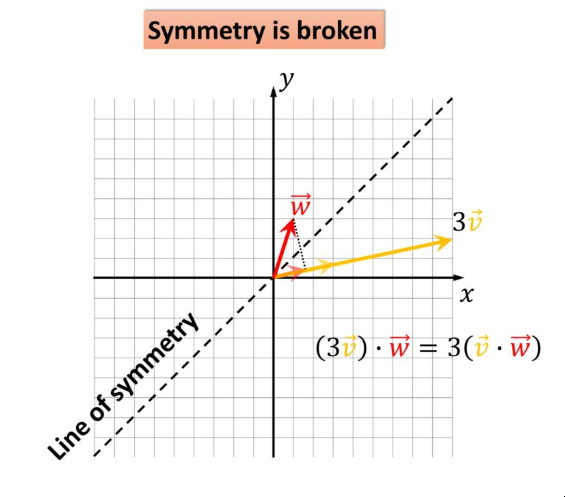
线性代数,对称线 让我们回想一下,使用标量缩放向量实际上是缩放其长度。
因此,我们可以观察到向量的大小与标量缩放的 vec{w} 相同。
现在,我们有一个标量乘以向量 vec{v},取 vec{w} 的内积与将 3 乘以 vec{v} 和 vec{w}相同。这说明内积确实是一种交换运算。
线性函数
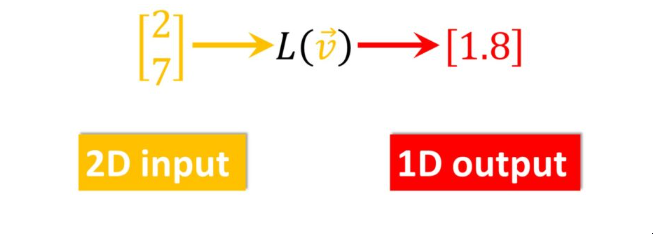
现在,我们将再次讨论线性函数。但是现在,我们将观察输入和输出维度不同的函数。例如,我们有一个 2D 输入向量,使用函数 L 它将为 1D 输出向量。
对于线性变换,以下属性确实成立:
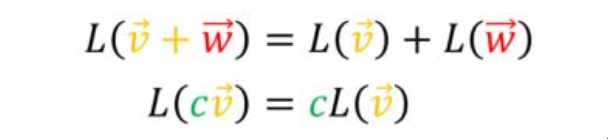
例如,一条带有均匀分布的点的线将被映射到一条 1D 线。在这里,请注意,实际上是将坐标为(x, y)的点映射到单个坐标在某条线上 z重要的是,映射线上的点之间的距离是等距的。这是线性变换的属性。
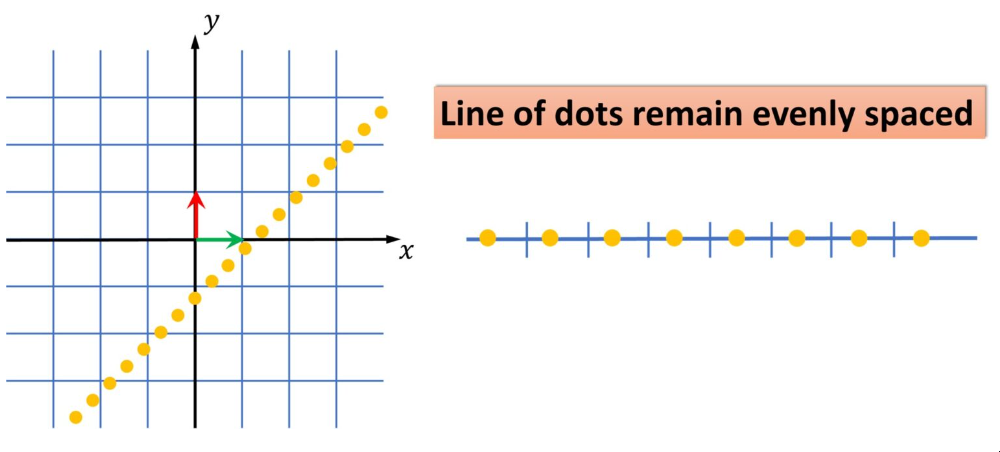
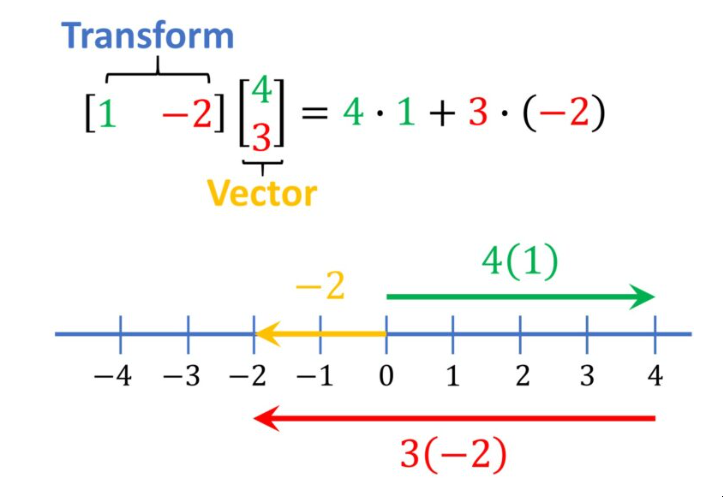
现在,观察在vec{w}向量上应用线性变换 [1 -2] 会发生什么?
它被映射,使其值为 -2, 转换将 2D 空间映射到一条线的一维空间。变换显示了如何映射单个基向量。
因此,-2 不改变 hat{i}向量(保持不变),但它会改变我们的 hat{j}向量。因此,使用任何向量都可以分解为基向量组合的想法,我们可以得到以下公式。
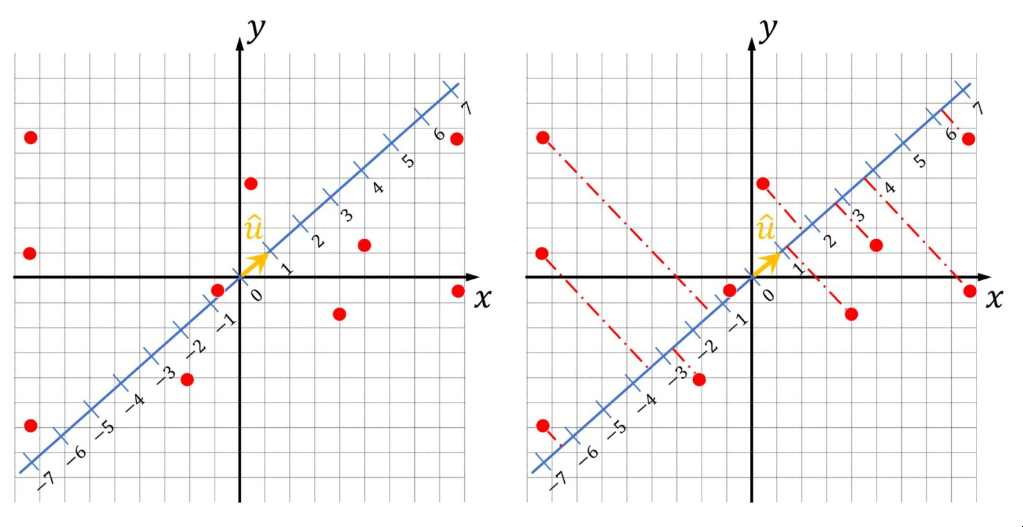
所有这些都可以在这个例子中澄清。你可以这样想:如何将二维点投影到一条线上。
我们有一个从 0 到 hat{u}的向量。
此外,我们还有很多 2D 点。我们感兴趣的是这些二维点(向量)将投影在一条线上的什么位置?
让我们看看hat{i}向量将落在定义这条线的单位向量hat{u}上。如果我们使用所谓的对称线,我们将得出结论,u_{x}将是一个投影 hat{i}。这也是向量hat{u}的 x–坐标。
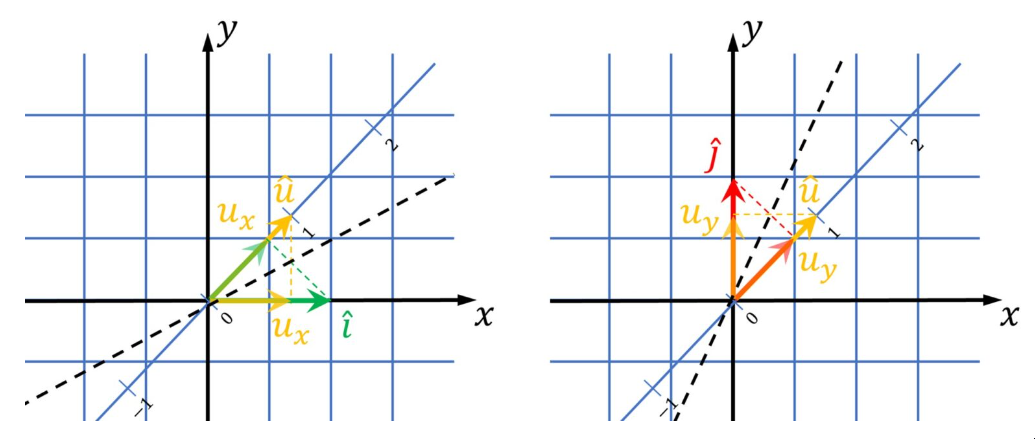
同样的情况也适用于向量hat{i}。它将被投影到一个长度为u_{y}的向量。所以,什么将是一个具有两个非零(x,y)坐标的任意矢量的投影。
我们看到u_{x} 和 u_{y} 定义了我们的投影矩阵。它们将告诉我们基向量的着陆点:u_{x}和 u_{y}
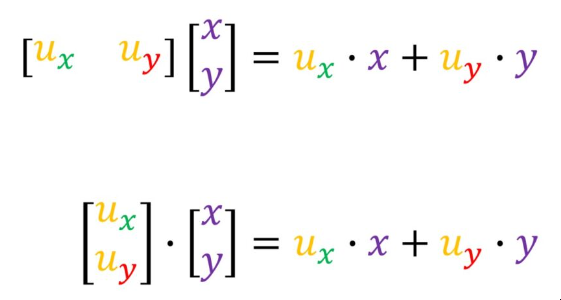
换句话说,如果我们用基向量表示我们的向量,我们会得到坐标(x, y)。
当我们将这些坐标分别与 u_{x} 和 u_{y} 相乘,然后将这两个乘积相加,我们将得到一个位置,在这个位置上,我们的原始(x, y)矢量将落在一条由矢量 hat{u} 定义的直线上。
这个位置,将是我们的新坐标,对于一个一维坐标系来说,就是 hat{u}。
第 3 步 编程工具
NumPy 的线性代数模块提供了多种方法将线性代数应用于任何 numpy 数组。 人们可以找到:
秩、行列式、跟踪等的数组
矩阵的特征值
矩阵和向量积(点积、内积、外积等)、矩阵幂
求解线性或张量方程等等!
线性代数是研究向量空间的数学分支。您将看到向量如何构成向量空间以及线性代数如何将线性变换应用于这些空间。
您还将学习线性方程组和矢量方程组之间的强大关系,这些关系与重要的数据科学概念,如最小二乘近似相关。
您最终将学习重要的矩阵分解方法:特征分解和奇异值分解 SVD,这对于理解主成分分析 PCA 等无监督学习方法非常重要。
本文由 mdnice 多平台发布