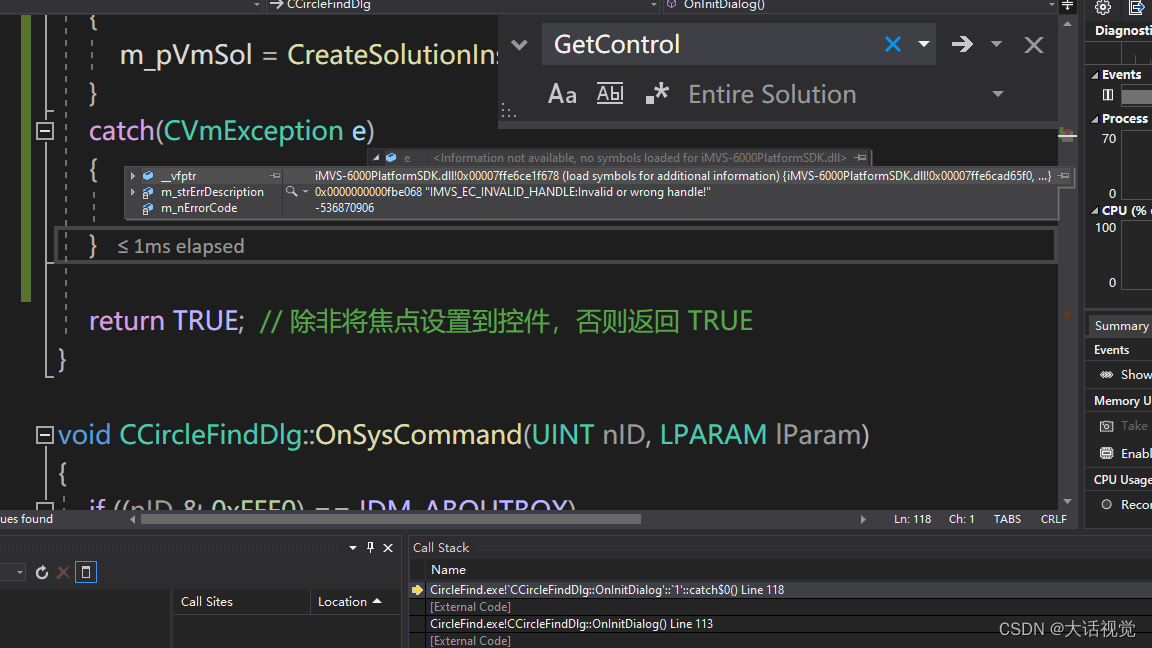
你还记得那条风靡全球的贪吃蛇吗？

我们在一个 n*n 的网格上构建了新的迷宫地图，蛇的长度为 2，也就是说它会占去两个单元格。蛇会从左上角（(0, 0) 和 (0, 1)）开始移动。我们用 0 表示空单元格，用 1 表示障碍物。蛇需要移动到迷宫的右下角（(n-1, n-2) 和 (n-1, n-1)）。

每次移动，蛇可以这样走：

• 如果没有障碍，则向右移动一个单元格。并仍然保持身体的水平／竖直状态。
• 如果没有障碍，则向下移动一个单元格。并仍然保持身体的水平／竖直状态。
• 如果它处于水平状态并且其下面的两个单元都是空的，就顺时针旋转 90 度。蛇从（(r, c)、(r, c+1)）移动到 （(r, c)、(r+1, c)）。

  

• 如果它处于竖直状态并且其右面的两个单元都是空的，就逆时针旋转 90 度。蛇从（(r, c)、(r+1, c)）移动到（(r, c)、(r, c+1)）。

  

返回蛇抵达目的地所需的最少移动次数。

如果无法到达目的地，请返回 -1。

示例 1：

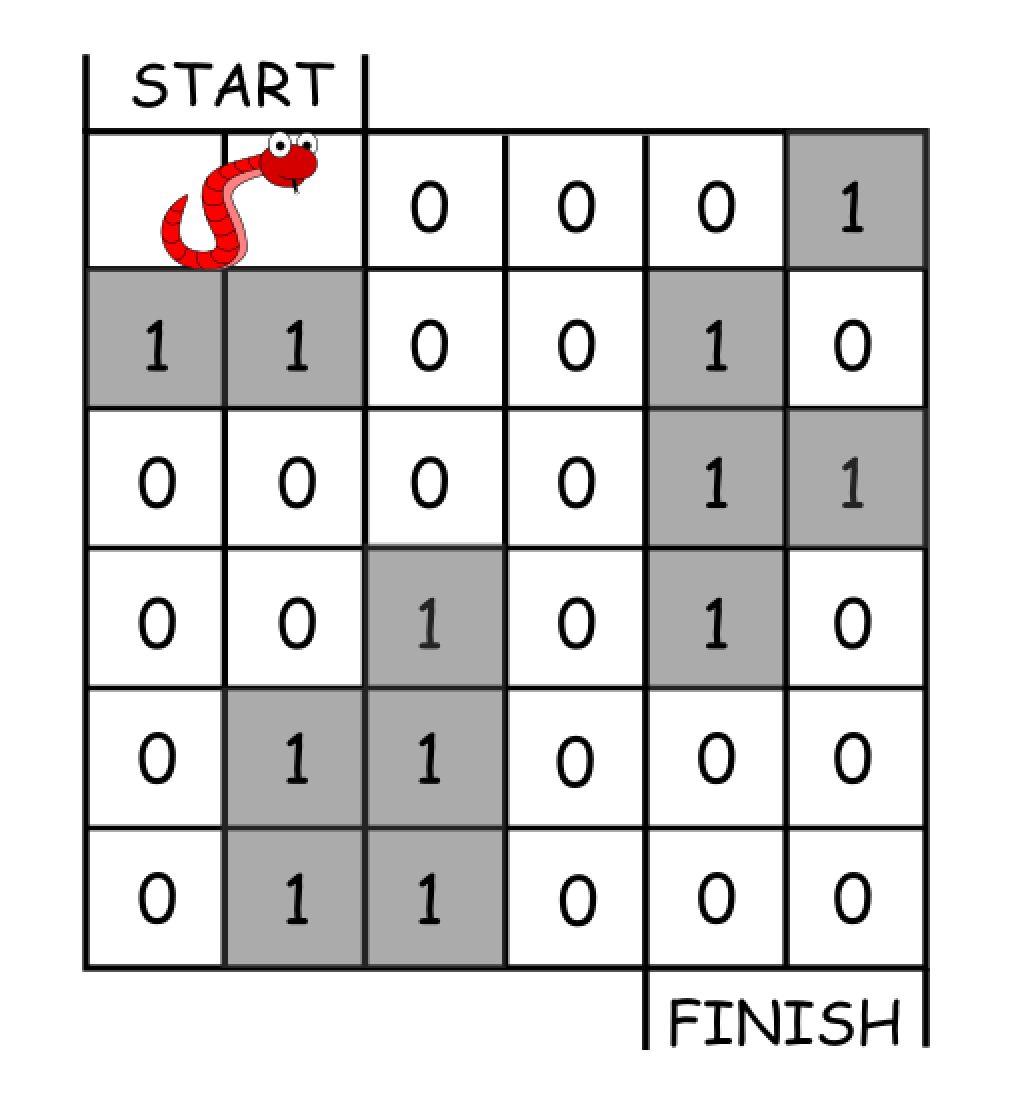
输入：grid = [[0,0,0,0,0,1],
               [1,1,0,0,1,0],
               [0,0,0,0,1,1],
               [0,0,1,0,1,0],
               [0,1,1,0,0,0],
               [0,1,1,0,0,0]]
输出：11
解释：
一种可能的解决方案是 [右, 右, 顺时针旋转, 右, 下, 下, 下, 下, 逆时针旋转, 右, 下]。

示例 2：

输入：grid = [[0,0,1,1,1,1],
               [0,0,0,0,1,1],
               [1,1,0,0,0,1],
               [1,1,1,0,0,1],
               [1,1,1,0,0,1],
               [1,1,1,0,0,0]]
输出：9

提示：

• 2 <= n <= 100
• 0 <= grid[i][j] <= 1
• 蛇保证从空单元格开始出发。

类似于走迷宫，运动人物从占一个格变成占两个格，运动方向从上下左右变成左右旋转，使用广度优先遍历解决此类问题，在同一个位置有三种方式行动，每次行动又会有新的位置生成，生成新的位置就会有新的运动路径(即三种方式)。使用队列将每次的三种方式都走一遍后将新的位置结点放入队列，并记录当前运动次数。直到循环结束，返回结果。

class Solution {
    public int minimumMoves(int[][] grid) {
        int n = grid.length;
        //记录每个结点的运动次数
        int[][][] dist = new int[n][n][2];
        for (int i = 0;i < n;i++){
            for (int j = 0;j < n;j++){
                //初始化数组
                Arrays.fill(dist[i][j],-1);
            }
        }
        ArrayDeque<int[]> queue = new ArrayDeque<>();
        dist[0][0][0] = 0;
        //队列中放入位置和当前横竖状态
        queue.offer(new int[]{0,0,0});
        while (!queue.isEmpty()){
            int[] arr = queue.poll();
            //位置参数
            int x = arr[0],y = arr[1],status = arr[2];
            //根据当前状态以及是否有空格位置判断下一步走向
            if (status == 0) {
                // 向右移动一个单元格
                if (y + 2 < n && dist[x][y + 1][0] == -1 && grid[x][y + 2] == 0) {
                    //运动次数++
                    dist[x][y + 1][0] = dist[x][y][0] + 1;
                    //将下一步的可执行路径放入到队列中
                    queue.offer(new int[]{x, y + 1, 0});
                }
                // 向下移动一个单元格
                if (x + 1 < n && dist[x + 1][y][0] == -1 && grid[x + 1][y] == 0 && grid[x + 1][y + 1] == 0) {
                    dist[x + 1][y][0] = dist[x][y][0] + 1;
                    queue.offer(new int[]{x + 1, y, 0});
                }
                // 顺时针旋转 90 度
                if (x + 1 < n && y + 1 < n && dist[x][y][1] == -1 && grid[x + 1][y] == 0 && grid[x + 1][y + 1] == 0) {
                    dist[x][y][1] = dist[x][y][0] + 1;
                    queue.offer(new int[]{x, y, 1});
                }
            } else {
                // 向右移动一个单元格
                if (y + 1 < n && dist[x][y + 1][1] == -1 && grid[x][y + 1] == 0 && grid[x + 1][y + 1] == 0) {
                    dist[x][y + 1][1] = dist[x][y][1] + 1;
                    queue.offer(new int[]{x, y + 1, 1});
                }
                // 向下移动一个单元格
                if (x + 2 < n && dist[x + 1][y][1] == -1 && grid[x + 2][y] == 0) {
                    dist[x + 1][y][1] = dist[x][y][1] + 1;
                    queue.offer(new int[]{x + 1, y, 1});
                }
                // 逆时针旋转 90 度
                if (x + 1 < n && y + 1 < n && dist[x][y][0] == -1 && grid[x][y + 1] == 0 && grid[x + 1][y + 1] == 0) {
                    dist[x][y][0] = dist[x][y][1] + 1;
                    queue.offer(new int[]{x, y, 0});
                }
            }
        }
        //返回移动次数，如果没有到达则会返回一个数组的初始化值-1
        return dist[n-1][n-2][0];
    }
}

 动态规划

力扣