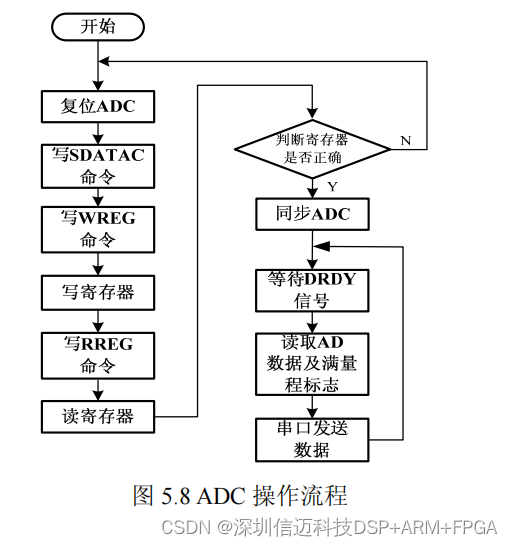
1 回归

             预测年薪  =   0.5 * 工作年限  +  0.7 * 学历数值

    回归的目的就是预测 数值型的目标值。         求解回归方程式 系数 （0.5 ，0.7）的过程就是 回归。  

2 简单线性回归

      样本特征只有一个的线性回归 ，称为简单线性回归。

     

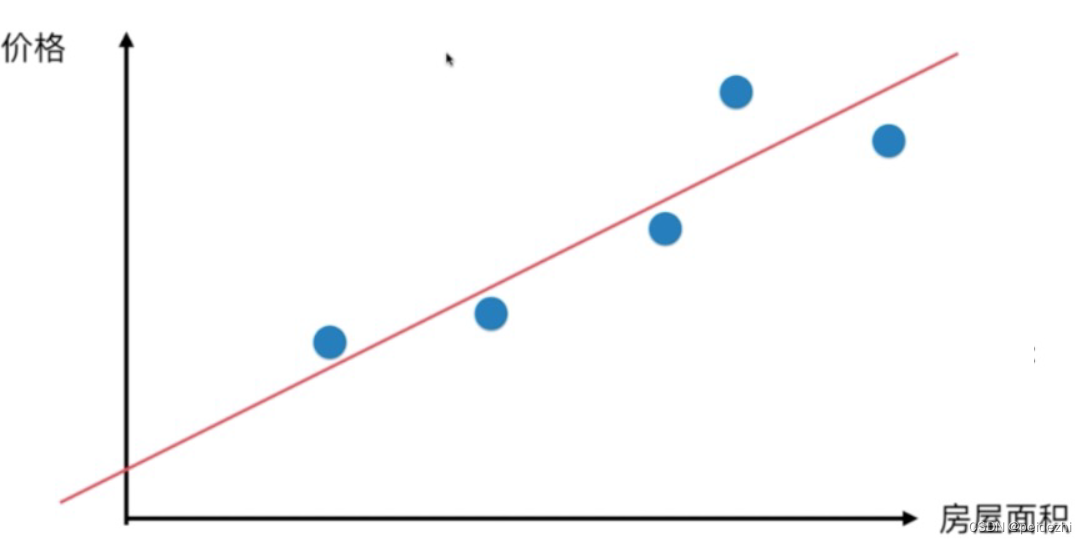
      举例： 房屋面积与价格的关系           y =   a x + b

  

   3 最小二乘法  

 第一个距离度量值可能为0 

第二个 非连续不可导，求解麻烦。

第三个 可导可度量。适合！！！

简单线性回归，  就是要找到参数a, b，  使y = ax +b ，对所有样本的误差的总和最小。

4 最小二乘法推导（台湾叫最小平方法法）

Loss= Σ (a𝑥i + 𝑏 − 𝑦i) ^2     

 Loss对b求导 （求b）

2 Σ (a𝑥i + 𝑏 − 𝑦i)  = 0       =>       

         同时除以N 

 即 

 

Loss对 a求导 （求a)

2 Σ (a𝑥i + 𝑏 − 𝑦i) * xi = 0         将 上一步得到的b带入       得到a       =>  

    

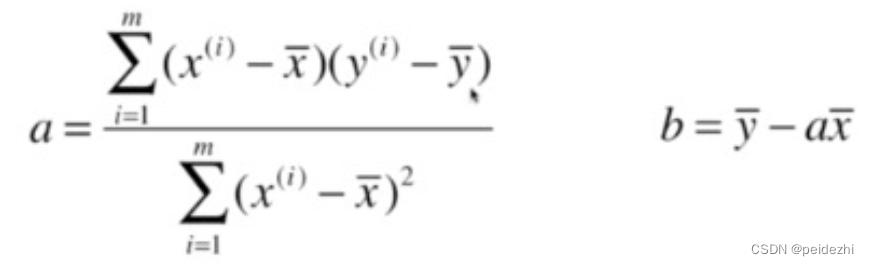
具体推导可参考：最小二乘法详细推导 - 知乎 

二、 多元线性回归

  1）概念

       多元线性回归如下图。（往往一个模型由多个变量来决定，而不是单个简单线性回归）

 

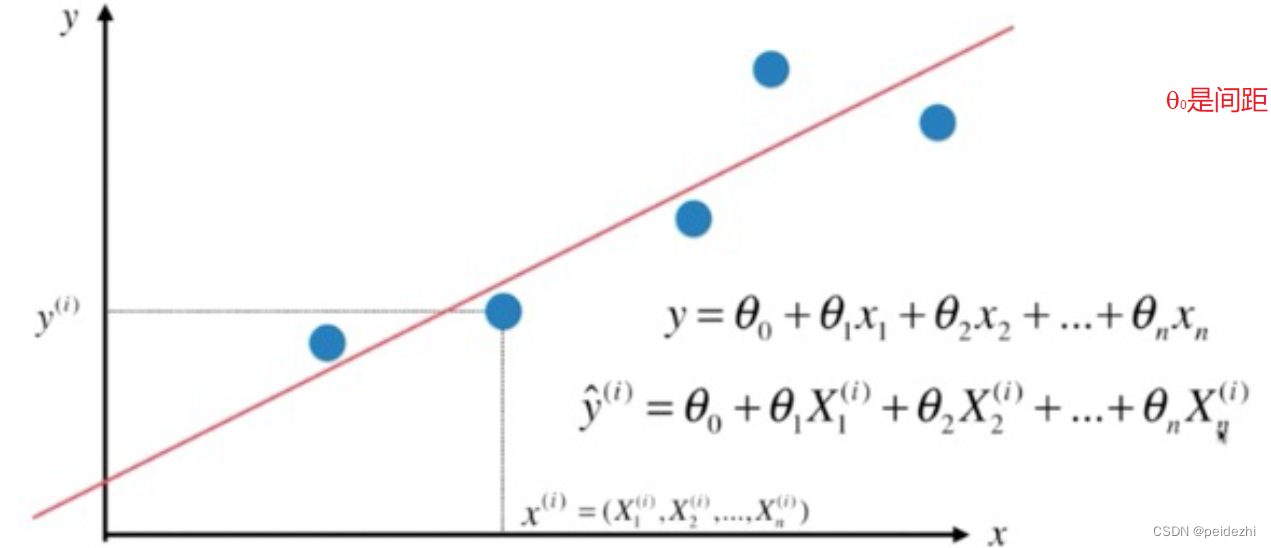
2 目标 

      目标即是找到一组参数。   所有样本的 误差平方和最小。即     

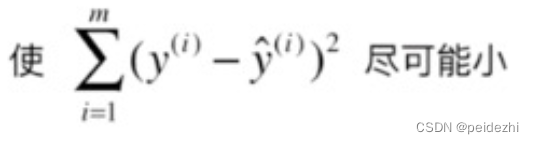
  其中：

                           

 

 3   推导：

      

 

 

       

 

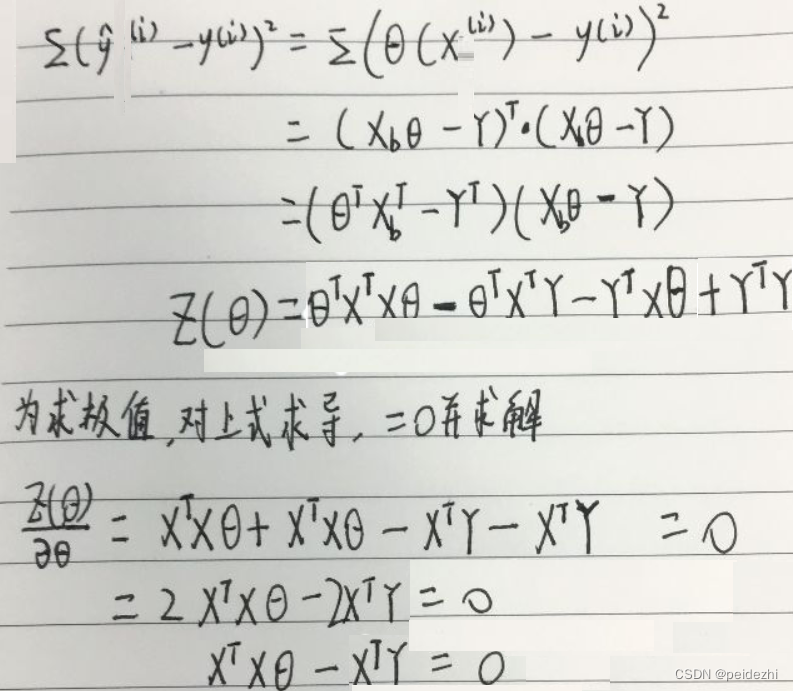
      最终得到： 

三、 回归算法 度量

 对于分类算法，我们可以使用 准确率acuracy和recall和f1-score来度量模型。

对于回归算法，怎么度量呢？

1 ）均方误差MSE( mean squared error)

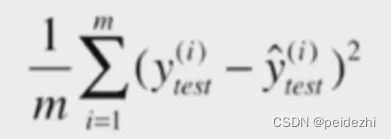
上述公式即为线性回归求解的损失函数（此处使用测试集，而非回归训练集），除以 总数m。

除以m， 表示平均。 避免同一模型，因测试数据数量差异导致上述结果 相差太大。

2）均方根误差RMSE( root mean squared error)

 

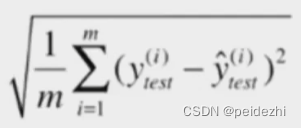
均方误差，会将数据值放大。比如房价预测，数值是万级别， 结果误差值会放大到 百万级别，同原始值没有可比性。

所以使用均方根误差RMSE 来将误差还原为同一数值级别。

3） 平均绝对误差MAE(mean absolute error)

MAE同 均方根误差比较类似。

4） R 方（R squared error) 。

 上面几个衡量标准对不同的模型，可能有不同的值范围。比如收入是几万，   预测身高可能是0.5 到2.0 米。    这怎么衡量模型到底好和坏呢？

分类模型，我们度量都是在0-1 的范围。 那么 回归模型是否有类似的衡量标准呢。

       答案是肯定的，   即是R方度量。

 

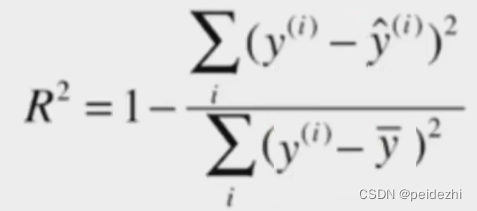
可以设想下： 

分母： 为 预测值 - 平均值，  平均值相当于一个不经过模型随便猜测都能得到的一个结果。

分子： 预测试 - 真实值  ，

             模型越好， 预测值越接近真实值，右边被减数 这个值越接近0.  则R方值 越接近 1

              模型越差，这个值越大， 则右边被减数越接近 1，  则R方值 越接近 0

因此 R方值【0，1】，可以按值大小评估回归模型。 越大越好。

5）SKLearn 使用R2

    from sklearn.metrics import r2_score

    r2_score(y_true ， y_predict）

     y_true, 标签值       y_predict模型预测值

注：

R2 =1.   表明， 我们的模型结果都与真实值一样。可能发生了过拟合。

R2 < 0,           说明我们的模型，还不如基准平均模型，很可能数据没有线性关系。

到这里标准线性回归就讲完了。  但是实际应用使用标准线性回归一般很少，都会使用Lasso\Ridge\ElasticNet

四、 Ridge 岭回归

     

 

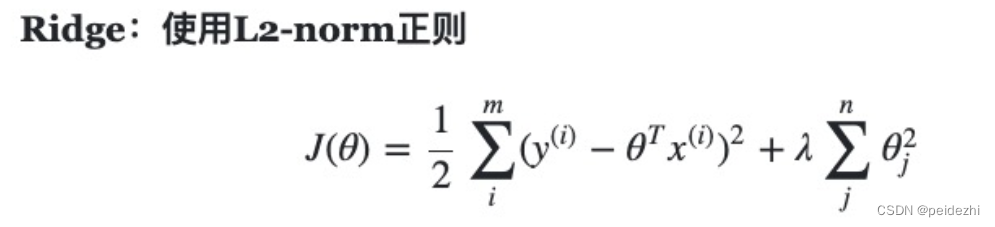
           岭回归最早用于解决特征数多于样本， ,    左侧不可逆，导致无解。        

注： 从数学上来看，  添加惩罚项，求解结果还是跟原来保持一致，只是求解范围更小了。

        数学上可以证明上式的等价形式如

          

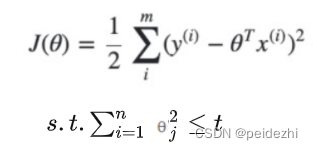
             损失函数跟线性回归还是一样， 只是参数的取值变的更小（求解空间平方和<=t）。

           标准线性回归，在使用普通最小二乘法回归的时候，当两个变量具有相关性的时候，可能会使得其中一个系数是个很大正数，另一个系数是很大的负数。通过岭回归的 参数平方和<=t限制，可以避免这个问题。

五、 LASSO回归

1） LASSO回归求解

              也称 L1-norm ，即1-范式

        

 

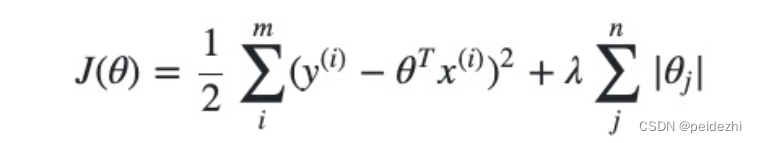
LASSO回归 使用了绝对值的一阶惩罚函数代替了Ridge岭回归 平方和的二阶函数。

LASSO回归求解结果如下：

  （坐标下降法求解过程参考：LASSO回归求解 - 知乎 ）视频：02-11-LASSO回归求解_哔哩哔哩_bilibili

            

  

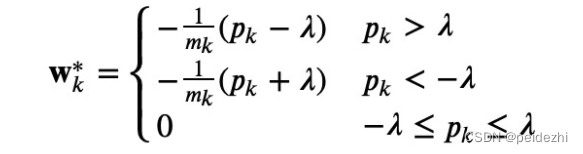
      m: 为特征维度         n为样本数 ， 其中

   

   

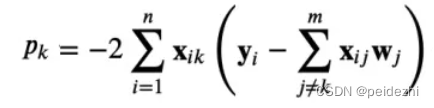
注： 上述求解时，可以先给定一个 值， 和一组 初始参数值 W = （0, 0, 0,..0)   [随机任意值，一般给0即可]

         求Wk  ：    先求Pk值,  Mk值，   看Pk取值范围，得到 具体的Wk

         遍历m次，即得到最终的m个参数 W* 

对Lasso回归，   值越大， 越来越多的参数越趋近于0。

2） Lasso回归优化：

可以看到上面Lasso回归求解时，  都是给定了一个，求得得参数基本能满足要求。

最终取多少，模型能得到W*最优呢？

可以使用交叉验证方法， 给定一组值，拿测试数据来校验误差得分，根据评价得分指标来得到最优。

i) 模型求解：

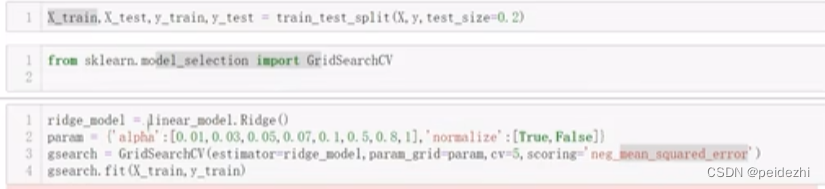
如下截图： GridSearchCV。 交叉验证各个 ,  将训练数据分成5折， 1折用来计算模型的均方误差值。误差最小的参数即为最佳参数。

ii) 模型评价：  

对于上述步骤求得的最佳参数（假如lamda=0.01，  normalize=True), 则最终模型如下图第一行，咱们可以把模型对训练数据和 测试数据（上述步骤预留20%）分别计算MSE值。

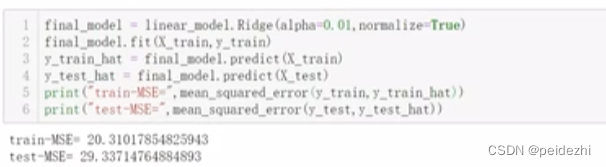
test集得到的MSE 29， 相比训练集得到的MSE 20, 相差比较大 。 咱们可能会认为模型过拟合，考虑优化。  重新选定 lamda=0.01为中心，给定一组 lamda的值，重新开始步骤 i） ii)， 反复迭代优化模型。