引言
EM算法是一种迭代算法,用于含有隐变量的概率模型参数的极大似然估计。
理解EM算法需要很多概率论的知识,所以下面先贴出所需要的知识。便于对后文的理解。
补充知识
期望
对于离散型随机变量
X
X
X的概率分布为
p
i
=
p
{
X
=
x
i
}
p_i=p\{X=x_i\}
pi=p{X=xi},期望
E
(
X
)
E(X)
E(X)为:
E
(
X
)
=
∑
i
x
i
p
i
E(X) = \sum_i x_i p_i
E(X)=i∑xipi
其中
p
i
p_i
pi是概率,满足两个条件
1
≤
p
i
≤
0
1 \leq p_i \leq 0
1≤pi≤0且
∑
i
p
i
=
1
\sum_i p_i =1
∑ipi=1。
若连续型随机变量
X
X
X的概率密度函数为
f
(
x
)
f(x)
f(x),则期望
E
(
X
)
E(X)
E(X)为:
E
(
X
)
=
∫
−
∞
+
∞
x
f
(
x
)
d
x
E(X) = \int_{-\infty}^{+\infty} xf(x)dx
E(X)=∫−∞+∞xf(x)dx
设
Y
=
g
(
X
)
Y=g(X)
Y=g(X),若
X
X
X是离散型随机变量,则:
E
(
Y
)
=
∑
i
g
(
x
i
)
p
i
E(Y)=\sum_i g(x_i)p_i
E(Y)=i∑g(xi)pi
若
X
X
X是连续型随机变量,则:
E
(
X
)
=
∫
−
∞
+
∞
g
(
x
)
f
(
x
)
d
x
E(X) = \int_{-\infty}^{+\infty} g(x)f(x)dx
E(X)=∫−∞+∞g(x)f(x)dx
C C C为常数, X X X和 Y Y Y是两个随机变量,以下是期望的性质:
- E ( C ) = C E(C) =C E(C)=C
- E ( C X ) = C E ( X ) E(CX) = CE(X) E(CX)=CE(X)
- E ( X + Y ) = E ( X ) + E ( Y ) E(X+Y) = E(X) + E(Y) E(X+Y)=E(X)+E(Y)
联合概率与边缘概率
假设有离散型随机变量X与Y
- P ( X = a , Y = b ) P(X=a,Y=b) P(X=a,Y=b)用于表示 X = a X=a X=a且 Y = b Y=b Y=b的概率,这种包含多个条件且所有条件同时成立的概率称为联合概率。
- 与之对应地, P ( X = a ) P(X=a) P(X=a)或 P ( Y = b ) P(Y=b) P(Y=b)这种只与单个随机变量有关的概率称为边缘概率。
联合概率一览表称为联合分布,边缘概率一览表称为边缘分布。
联合概率与边缘概率的关系如下:
P
(
X
=
a
)
=
∑
b
P
(
X
=
a
,
Y
=
b
)
P(X=a) = \sum_b P(X=a,Y=b)
P(X=a)=b∑P(X=a,Y=b)
上式相当于是固定
X
X
X,
Y
Y
Y取所有的取值(
Y
Y
Y跑一圈)。也可以固定
Y
Y
Y,让
X
X
X取所有的值:
P
(
Y
=
b
)
=
∑
a
P
(
X
=
a
,
Y
=
b
)
P(Y=b) = \sum_a P(X=a,Y=b)
P(Y=b)=a∑P(X=a,Y=b)
来看一下简单的题理解一下。
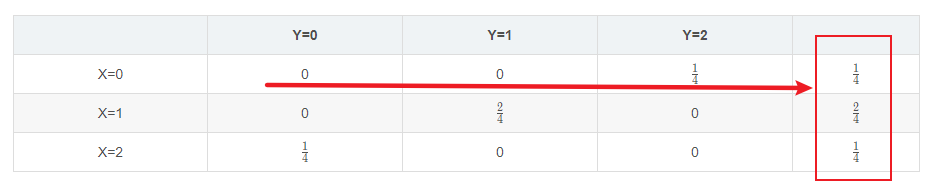
例题1.抛两枚硬币(出现正反面的概率皆为50%),且随机变量X,Y分别表示正面及反面出现的次数,求X与Y的联合概率及X的边缘概率。
这是离散型的,我们可以写出所有可能:(正,正)、(正,反)、(反,正)、(反,反)
然后画一个表格,写出所有可能的概率。
| Y=0 | Y=1 | Y=2 | |
|---|---|---|---|
| X=0 | 0 | 0 | 1 4 \frac{1}{4} 41 |
| X=1 | 0 | 2 4 \frac{2}{4} 42 | 0 |
| X=2 | 1 4 \frac{1}{4} 41 | 0 | 0 |
这个就是X与Y的联合分布。
X的边缘分布则为:
其中
P
(
X
=
0
)
=
P
(
X
=
0
,
Y
=
0
)
+
P
(
X
=
0
,
Y
=
1
)
+
P
(
X
=
0
,
Y
=
2
)
=
0
+
0
+
1
4
=
1
4
P(X=0)=P(X=0,Y=0)+P(X=0,Y=1)+P(X=0,Y=2)=0+0+\frac{1}{4}=\frac{1}{4}
P(X=0)=P(X=0,Y=0)+P(X=0,Y=1)+P(X=0,Y=2)=0+0+41=41
我们可以像上面这样通过联合分布计算边缘分布。
联合分布还有一条性质就是:
∑
a
∑
b
P
(
X
=
a
,
Y
=
b
)
=
1
\sum_a\sum_b P(X=a,Y=b)=1
a∑b∑P(X=a,Y=b)=1
条件概率
条件概率的定义为:
P
(
Y
=
b
∣
X
=
a
)
=
P
(
X
=
a
,
Y
=
b
)
P
(
X
=
a
)
P(Y=b|X=a) = \frac{P(X=a,Y=b)}{P(X=a)}
P(Y=b∣X=a)=P(X=a)P(X=a,Y=b)
条件概率有如下性质:
在条件
Y
=
b
Y=b
Y=b下
X
X
X的条件分布也是一种"X的概率分布",因此穷举
X
X
X可取的值后,所有这些值对应的概率之和为
1
1
1。即:
∑
a
P
(
X
=
a
∣
Y
=
b
)
=
1
\sum_a P(X=a|Y=b) = 1
a∑P(X=a∣Y=b)=1
要看清楚 X X X和 Y Y Y哪个是条件,如果是 ∑ a P ( Y = b ∣ X = a ) \sum_a P(Y=b|X=a) ∑aP(Y=b∣X=a)的值,则不一定是1。
下面简单地证明下上式:
∑
a
P
(
X
=
a
∣
Y
=
b
)
=
∑
a
P
(
X
=
a
,
Y
=
b
)
P
(
Y
=
b
)
=
P
(
Y
=
b
)
P
(
Y
=
b
)
=
1
\sum_a P(X=a|Y=b) = \frac{ \sum_a P(X=a,Y=b)}{P(Y=b)} = \frac{P(Y=b)}{P(Y=b)} = 1
a∑P(X=a∣Y=b)=P(Y=b)∑aP(X=a,Y=b)=P(Y=b)P(Y=b)=1
三个或更多的随机变量
含有三个或更多的随机变量时,条件概率的定义依然与之前相同。
- Y = b Y=b Y=b且 Z = c Z=c Z=c时, X = a X=a X=a的条件概率
P ( X = a ∣ Y = b , Z = c ) = P ( X = a , Y = b , Z = c ) P ( Y = b , Z = c ) P(X=a|Y=b,Z=c) = \frac{P(X=a,Y=b,Z=c)}{P(Y=b,Z=c)} P(X=a∣Y=b,Z=c)=P(Y=b,Z=c)P(X=a,Y=b,Z=c)
- Z = c Z=c Z=c时, X = a X=a X=a且 Y = b Y=b Y=b的条件概率
P ( X = a , Y = b ∣ Z = c ) = P ( X = a , Y = b , Z = c ) P ( Z = c ) P(X=a,Y=b|Z=c) = \frac{P(X=a,Y=b,Z=c)}{P(Z=c)} P(X=a,Y=b∣Z=c)=P(Z=c)P(X=a,Y=b,Z=c)
通常,我们可以像下面这样分解联合概率。
P
(
X
=
a
,
Y
=
b
,
Z
=
c
)
=
P
(
X
=
a
∣
Y
=
b
,
Z
=
c
)
P
(
Y
=
b
∣
Z
=
c
)
P
(
Z
=
c
)
P(X=a,Y=b,Z=c)=P(X=a|Y=b,Z=c)P(Y=b|Z=c)P(Z=c)
P(X=a,Y=b,Z=c)=P(X=a∣Y=b,Z=c)P(Y=b∣Z=c)P(Z=c)
☆条件联合分布的分解☆
标了☆表示这个是重点,上面说了这么多,就是为了引入这一小节。
P
(
X
=
a
,
Y
=
b
∣
Z
=
c
)
=
P
(
X
=
a
∣
Y
=
b
,
Z
=
c
)
P
(
Y
=
b
∣
Z
=
c
)
(p1)
P(X=a,Y=b|Z=c) = P(X=a|Y=b,Z=c)P(Y=b|Z=c) \tag{p1}
P(X=a,Y=b∣Z=c)=P(X=a∣Y=b,Z=c)P(Y=b∣Z=c)(p1)
乍一看好像两边不相等,但是看完这一小节后,保证你乍一看,两边就是相等的。
上式
(
p
1
)
(p1)
(p1)左侧为
P
(
X
=
a
,
Y
=
b
,
Z
=
c
)
P
(
Z
=
c
)
\frac{P(X=a,Y=b,Z=c)}{P(Z=c)}
P(Z=c)P(X=a,Y=b,Z=c)
(
p
1
)
(p1)
(p1)右侧可以写为(为右侧两项分别应用条件概率的定义):
P
(
X
=
a
,
Y
=
b
,
Z
=
c
)
P
(
Y
=
b
,
Z
=
c
)
⋅
P
(
Y
=
b
,
Z
=
c
)
P
(
Z
=
c
)
=
P
(
X
=
a
,
Y
=
b
,
Z
=
c
)
P
(
Z
=
c
)
\frac{P(X=a,Y=b,Z=c)}{P(Y=b,Z=c)}\cdot \frac{P(Y=b,Z=c)}{P(Z=c)} = \frac{P(X=a,Y=b,Z=c)}{P(Z=c)}
P(Y=b,Z=c)P(X=a,Y=b,Z=c)⋅P(Z=c)P(Y=b,Z=c)=P(Z=c)P(X=a,Y=b,Z=c)
这样就证明了等式
(
p
1
)
(p1)
(p1)的成立,也可以把等式两边同乘以
P
(
Z
=
c
)
P(Z=c)
P(Z=c)来证明。
还可以换一种方式来理解, ( p 1 ) (p1) (p1)式中每一个 P P P都附有 Z = c Z=c Z=c的条件。即条件 Z = c Z=c Z=c是整个式子的大前提。因此,我们可以先声明这一前提,表示之后将基于这一大前提分解概率,而不必每次强调 Z = c Z=c Z=c。
于是,就转化为了以下式子:
P
(
X
=
a
,
Y
=
b
)
=
P
(
X
=
a
∣
Y
=
b
)
P
(
Y
=
b
)
P(X=a,Y=b) = P(X=a|Y=b) P(Y=b)
P(X=a,Y=b)=P(X=a∣Y=b)P(Y=b)
好了,下面正式进入EM算法的理解。
Jensen不等式
Jensen不等式和凸函数的定义有关。首先看凸函数的定义。
设
C
C
C是非空凸集,
f
f
f是定义在
C
C
C上的函数,如果对任意的
x
1
,
x
2
∈
C
,
λ
∈
(
0
,
1
)
x_1,x_2 \in C, \lambda\in (0,1)
x1,x2∈C,λ∈(0,1),均有:
f
(
λ
x
1
+
(
1
−
λ
)
x
2
)
≤
λ
f
(
x
1
)
+
(
1
−
λ
)
f
(
x
2
)
(p2)
f(\lambda x_1 + (1-\lambda)x_2) \leq \lambda f(x_1) + (1-\lambda) f(x_2) \tag{p2}
f(λx1+(1−λ)x2)≤λf(x1)+(1−λ)f(x2)(p2)
则称
f
f
f为
C
C
C上的凸函数;
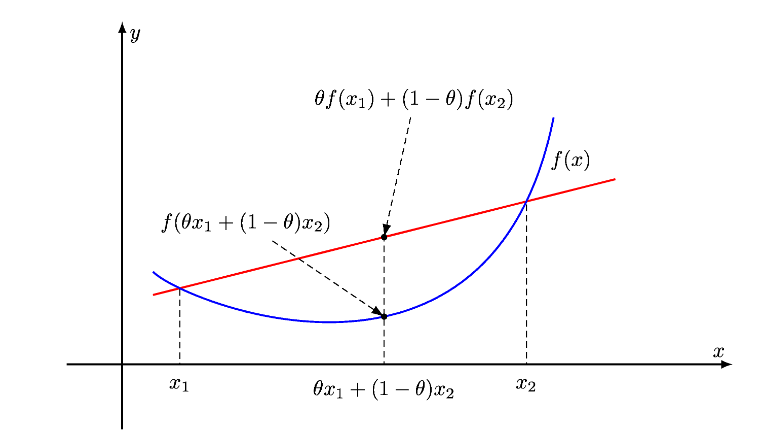
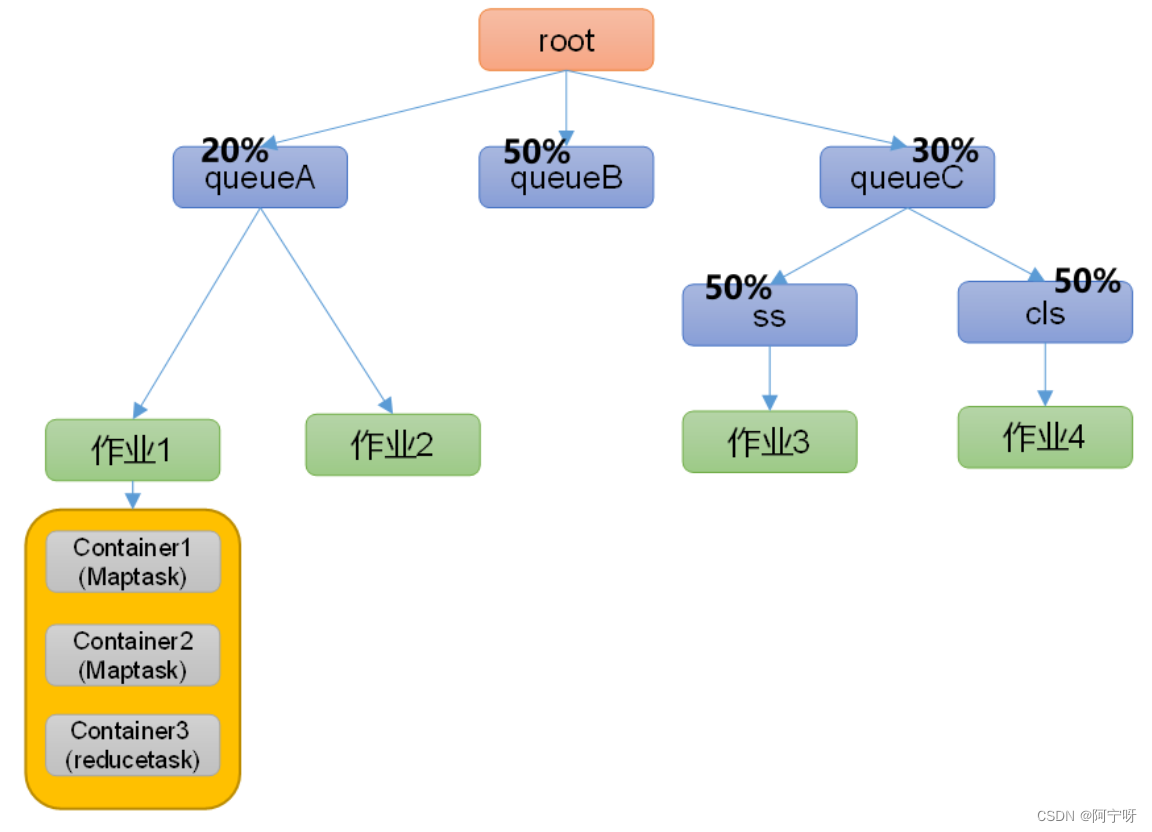
如上图所示( θ \theta θ即 λ \lambda λ),即凸函数任意两点之间直线位于两点之间曲线的上方。
这也是Jensen不等式的两点形式,我们可以将其推广到一般的情况,即:
f
(
∑
i
=
1
n
λ
i
x
i
)
≤
∑
i
=
1
n
λ
i
f
(
x
i
)
)
f(\sum_{i=1}^n \lambda_i x_i) \leq \sum_{i=1}^n \lambda_i f(x_i))
f(i=1∑nλixi)≤i=1∑nλif(xi))
其中
∑
i
=
1
n
λ
i
=
1
\sum_{i=1}^n \lambda_i=1
∑i=1nλi=1。
如果为凹函数,则不等式符号取反,有:
f
(
∑
i
=
1
n
λ
i
x
i
)
≥
∑
i
=
1
n
λ
i
f
(
x
i
)
)
f(\sum_{i=1}^n \lambda_i x_i) \geq \sum_{i=1}^n \lambda_i f(x_i))
f(i=1∑nλixi)≥i=1∑nλif(xi))
下面我们来证明一下。对于 n = 2 n=2 n=2的情况,由凸函数的定义,已经成立了。
下面,我们通过数学归纳法的思想来证明。
假设在
n
=
k
n=k
n=k的情况下,不等式成立,即
f
(
∑
i
=
1
k
λ
i
x
i
)
≤
∑
i
=
1
k
λ
i
f
(
x
i
)
(p3)
f(\sum_{i=1}^k \lambda_i x_i) \leq \sum_{i=1}^k \lambda_i f(x_i) \tag{p3}
f(i=1∑kλixi)≤i=1∑kλif(xi)(p3)
成立。
下面我们来证明当
n
=
k
+
1
n=k+1
n=k+1时,公式仍然成立,即
f
(
∑
i
=
1
k
+
1
λ
i
x
i
)
≤
∑
i
=
1
k
+
1
λ
i
f
(
x
i
)
)
f(\sum_{i=1}^{k+1} \lambda_i x_i) \leq \sum_{i=1}^{k+1} \lambda_i f(x_i))
f(i=1∑k+1λixi)≤i=1∑k+1λif(xi))
首先把函数里面
k
+
1
k+1
k+1个数分成两部分,
∑
i
=
1
k
+
1
λ
i
x
i
=
∑
i
=
1
k
λ
i
x
i
+
λ
k
+
1
x
k
+
1
=
(
1
−
λ
k
+
1
)
∑
i
=
1
k
λ
i
1
−
λ
k
+
1
x
i
+
λ
k
+
1
x
k
+
1
\begin{aligned} \sum_{i=1}^{k+1} \lambda_i x_i &= \sum_{i=1}^k \lambda_i x_i + \lambda_{k+1} x_{k+1} \\ &= (1-\lambda_{k+1}) \sum_{i=1}^k \frac{\lambda_i}{1-\lambda_{k+1}} x_i + \lambda_{k+1} x_{k+1} \end{aligned}
i=1∑k+1λixi=i=1∑kλixi+λk+1xk+1=(1−λk+1)i=1∑k1−λk+1λixi+λk+1xk+1
令
x
∗
=
∑
i
=
1
k
λ
i
1
−
λ
k
+
1
x
i
x^* = \sum_{i=1}^k \frac{\lambda_i}{1 - \lambda_{k+1}} x_i
x∗=∑i=1k1−λk+1λixi,则:
f
(
∑
i
=
1
k
+
1
λ
i
x
i
)
=
f
(
(
1
−
λ
k
+
1
)
x
∗
+
λ
k
+
1
x
k
+
1
)
f\left( \sum_{i=1}^{k+1} \lambda_i x_i \right) = f( (1-\lambda_{k+1})x^* + \lambda_{k+1}x_{k+1} )
f(i=1∑k+1λixi)=f((1−λk+1)x∗+λk+1xk+1)
x
∗
x^*
x∗相当于一个新的点,而
1
−
λ
k
+
1
+
λ
k
+
1
=
1
1-\lambda_{k+1} + \lambda_{k+1}=1
1−λk+1+λk+1=1,变成了满足公式
(
p
2
)
(p2)
(p2)的形式,因此代入得:
f
(
∑
i
=
1
k
+
1
λ
i
x
i
)
=
f
(
(
1
−
λ
k
+
1
)
x
∗
+
λ
k
+
1
x
k
+
1
)
≤
(
1
−
λ
k
+
1
)
f
(
x
∗
)
+
λ
k
+
1
f
(
x
k
+
1
)
=
(
1
−
λ
k
+
1
)
f
(
∑
i
=
1
k
λ
i
1
−
λ
k
+
1
x
i
)
+
λ
k
+
1
f
(
x
k
+
1
)
(p4)
\begin{aligned} f\left( \sum_{i=1}^{k+1} \lambda_i x_i \right) &= f( (1-\lambda_{k+1})x^* + \lambda_{k+1}x_{k+1} ) \\ &\leq (1-\lambda_{k+1}) f(x^*) +\lambda_{k+1} f(x_{k+1}) \\ &= (1-\lambda_{k+1}) f\left( \sum_{i=1}^k \frac{\lambda_i}{1 - \lambda_{k+1}} x_i \right) +\lambda_{k+1} f(x_{k+1}) \end{aligned} \tag{p4}
f(i=1∑k+1λixi)=f((1−λk+1)x∗+λk+1xk+1)≤(1−λk+1)f(x∗)+λk+1f(xk+1)=(1−λk+1)f(i=1∑k1−λk+1λixi)+λk+1f(xk+1)(p4)
下面我们针对函数中求和这一项,我们假设
n
=
k
+
1
n=k+1
n=k+1,因此有
∑
i
=
1
k
λ
i
+
λ
k
+
1
=
1
\sum_{i=1}^k \lambda_i + \lambda_{k+1}=1
∑i=1kλi+λk+1=1,即有
∑
i
=
1
k
λ
i
1
−
λ
k
+
1
=
1
\sum_{i=1}^k \frac{\lambda_i}{1-\lambda_{k+1}}=1
∑i=1k1−λk+1λi=1成立,根据公式
(
p
3
)
(p3)
(p3),有:
f
(
∑
i
=
1
k
λ
i
1
−
λ
k
+
1
x
i
)
≤
∑
i
=
1
k
λ
i
1
−
λ
k
+
1
f
(
x
i
)
f\left( \sum_{i=1}^k \frac{\lambda_i}{1 - \lambda_{k+1}} x_i \right) \leq \sum_{i=1}^k \frac{\lambda_i}{1 - \lambda_{k+1}} f(x_i)
f(i=1∑k1−λk+1λixi)≤i=1∑k1−λk+1λif(xi)
把该结果代入
(
p
4
)
(p4)
(p4),则有:
f
(
∑
i
=
1
k
+
1
λ
i
x
i
)
≤
(
1
−
λ
k
+
1
)
(
∑
i
=
1
k
λ
i
1
−
λ
k
+
1
f
(
x
i
)
)
+
λ
k
+
1
f
(
x
k
+
1
)
=
∑
i
=
1
k
λ
i
f
(
x
i
)
+
λ
k
+
1
f
(
x
k
+
1
)
=
∑
i
=
1
k
+
1
λ
i
f
(
x
i
)
\begin{aligned} f\left( \sum_{i=1}^{k+1} \lambda_i x_i \right) &\leq (1-\lambda_{k+1})\left( \sum_{i=1}^k \frac{\lambda_i}{1 - \lambda_{k+1}} f(x_i)\right) +\lambda_{k+1} f(x_{k+1}) \\ &= \sum_{i=1} ^k \lambda_i f(x_i) + \lambda_{k+1} f(x_{k+1}) \\ &= \sum_{i=1} ^{k+1} \lambda_i f(x_i) \end{aligned}
f(i=1∑k+1λixi)≤(1−λk+1)(i=1∑k1−λk+1λif(xi))+λk+1f(xk+1)=i=1∑kλif(xi)+λk+1f(xk+1)=i=1∑k+1λif(xi)
上面
1
1
−
λ
k
+
1
\frac{1}{1-\lambda_{k+1}}
1−λk+11与求和中的
i
i
i无关,可以提到求和符号外面,刚好与外面的
1
−
λ
k
+
1
1-\lambda_{k+1}
1−λk+1相乘得1。证毕。
对于对数函数,即
f
(
⋅
)
f(\cdot)
f(⋅)为
log
(
⋅
)
\log(\cdot)
log(⋅),注意
log
\log
log函数为凹函数,因此我们可以写成对应的Jensen不等式:
log
(
∑
i
=
1
n
λ
i
x
i
)
≥
∑
i
=
1
n
λ
i
log
(
x
i
)
\log (\sum_{i=1}^n \lambda_i x_i) \geq \sum_{i=1}^n \lambda_i \log (x_i)
log(i=1∑nλixi)≥i=1∑nλilog(xi)
EM算法的引入
EM算法是含有隐变量的概率模型参数的极大似然估计法。
EM算法
首先介绍一个使用EM算法的例子。
例9.1
假设有3 枚硬币,分别记作A,B,C。这些硬币正面出现的概率分别是
π
\pi
π,
p
p
p 和
q
q
q。进行如下掷硬币试验: 先掷硬币A ,根据其结果选出硬币B或硬币C ,正面选硬币B ,反面边硬币C; 然后掷选出的硬币,掷硬币的结果,出现正面记作1,出现反面记作0; 独立地重复n 次试验(这里, n= 10) ,观测结果如下:
1
,
1
,
0
,
1
,
0
,
0
,
1
,
0
,
1
,
1
1,1,0,1,0,0,1,0,1,1
1,1,0,1,0,0,1,0,1,1
假设只能观测到掷硬币的结果,不能观测掷硬币的过程。问如何估计三硬币正面出现的概率,即三硬币模型的参数(即 π , p , q \pi,p,q π,p,q)。
三硬币模型可以写作
P
(
y
∣
θ
)
=
∑
z
P
(
y
,
z
∣
θ
)
=
∑
z
P
(
z
∣
θ
)
P
(
y
∣
z
,
θ
)
=
π
p
y
(
1
−
p
)
1
−
y
+
(
1
−
π
)
q
y
(
1
−
q
)
1
−
y
(9.1)
\begin{aligned} P(y|\theta) &= \sum_z P(y,z|\theta) = \sum_z P(z|\theta) P(y|z,\theta) \\ &= \pi p^y (1-p)^{1-y} + (1-\pi)q^y (1-q)^{1-y} \end{aligned} \tag{9.1}
P(y∣θ)=z∑P(y,z∣θ)=z∑P(z∣θ)P(y∣z,θ)=πpy(1−p)1−y+(1−π)qy(1−q)1−y(9.1)
这里,随机变量
y
y
y是观测变量,表示一次试验观测的结果是1 或0; 随机变量
z
z
z是隐变量,表示未观测到的掷硬币A 的结果;
θ
=
(
π
,
p
,
q
)
\theta =(\pi,p,q)
θ=(π,p,q)是模型参数。这一模型是以上数据的生成模型。注意,随机变量
y
y
y的数据可以观测,随机变量
z
z
z 的数据不可观测。
第一次看到这个式子,半天没明白,然后只能跑回去补概率论的知识。下面写出本人的理解,如有误,请斧正。
首先
P
(
y
∣
θ
)
=
∑
z
P
(
y
,
z
∣
θ
)
P(y|\theta) = \sum_z P(y,z|\theta)
P(y∣θ)=∑zP(y,z∣θ)。这个式子左右两边条件中都有一个
θ
\theta
θ,我们可以去掉它,就是联合概率和边缘概率关系的式子。也可以进行简单的证明。
P
(
y
∣
θ
)
=
∑
z
P
(
y
,
z
∣
θ
)
P
(
y
,
θ
)
P
(
θ
)
=
∑
z
P
(
y
,
z
,
θ
)
P
(
θ
)
P
(
y
,
θ
)
P
(
θ
)
=
P
(
y
,
θ
)
P
(
θ
)
\begin{aligned} & P(y|\theta) = \sum_z P(y,z|\theta) \\ & \frac{P(y,\theta)}{P(\theta)} = \frac{ \sum_z P(y,z,\theta)}{P(\theta)}\\ & \frac{P(y,\theta)}{P(\theta)} = \frac{P(y,\theta)}{P(\theta)} \\ \end{aligned}
P(y∣θ)=z∑P(y,z∣θ)P(θ)P(y,θ)=P(θ)∑zP(y,z,θ)P(θ)P(y,θ)=P(θ)P(y,θ)
而对于
∑
z
P
(
y
,
z
∣
θ
)
=
∑
z
P
(
z
∣
θ
)
P
(
y
∣
z
,
θ
)
\sum_z P(y,z|\theta) = \sum_z P(z|\theta) P(y|z,\theta)
∑zP(y,z∣θ)=∑zP(z∣θ)P(y∣z,θ)则是补充知识中条件联合分布的分解这一小节介绍的内容。条件中都有
θ
\theta
θ,我们直接去掉它,就好理解了,这里就不证明了。
下面来看式
(
9.1
)
(9.1)
(9.1)最后一个等式是怎么来的。
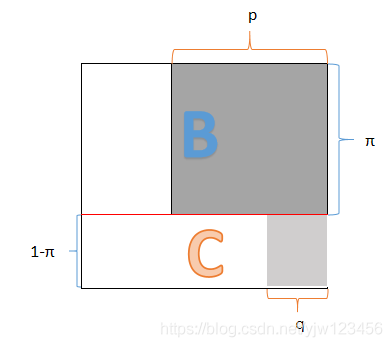
(上图参考了程序员的数学2 概率论)
我们可以画一个类似上面的正方形来理解,把概率转换为面积的思想来理解,整个正方形的面积为1。首先在该正方形中间画一条红线,分成了两个矩阵。
A硬币出现正面的概率为
π
\pi
π(这只是一个符号,所有的概率都是
[
0
,
1
]
[0,1]
[0,1]之间,不是圆周率那个
π
\pi
π),它就占了红线上方的那个矩形。A硬币出现反面的概率就是
1
−
π
1-\pi
1−π,即线色下面那个矩形。
在A正的情况下,硬币B正面概率为
p
p
p,就是上图深灰色区域。在A反的情况下,C正的概率为
q
q
q,为上图浅灰色区域。
式
(
9.1
)
(9.1)
(9.1)是一次试验的结果。
y
y
y为观测结果,
y
y
y要么为0要么为1。
- 当y=1时,这次实验的概率就是上图灰色面积之和:
π p + ( 1 − π ) q \pi p + (1-\pi)q πp+(1−π)q
- 当y=0时,这次实验的概率就是上图白色面积之和:
π ( 1 − p ) + ( 1 − π ) ( 1 − q ) \pi (1-p) + (1-\pi)(1-q) π(1−p)+(1−π)(1−q)
写到一起就是最终的等式。
也可以直接根据
∑
z
P
(
z
∣
θ
)
P
(
y
∣
z
,
θ
)
\sum_z P(z|\theta) P(y|z,\theta)
∑zP(z∣θ)P(y∣z,θ)写出最终结果,这里
θ
\theta
θ是固定的,可以先不看。
P
(
z
=
1
)
P(z=1)
P(z=1)就是
π
\pi
π,
P
(
z
=
0
)
=
1
−
π
P(z=0) = 1- \pi
P(z=0)=1−π。
乘以
P
(
y
∣
z
)
P(y|z)
P(y∣z),若
z
=
1
z=1
z=1,则考虑硬币B。根据
y
y
y的观测结果,则乘以硬币B相应的概率
p
p
p或
1
−
p
1-p
1−p。写到一起也可以得到
π
p
y
(
1
−
p
)
1
−
y
\pi p^y(1-p)^{1-y}
πpy(1−p)1−y。
当y=1时, π p y ( 1 − p ) 1 − y \pi p^y(1-p)^{1-y} πpy(1−p)1−y就是 π p \pi p πp;当y=0时,就是 π ( 1 − p ) \pi (1-p) π(1−p)。虽然写到了一起,但是根据实际结果只会出现一个。
所以将观测数据表示为 Y = ( Y 1 , Y 2 , ⋯ , Y n ) T Y=(Y_1,Y_2,\cdots,Y_n)^T Y=(Y1,Y2,⋯,Yn)T ,未观测数据表示为 Z = ( Z 1 , Z 2 , ⋯ , Z n ) T Z=(Z_1,Z_2,\cdots,Z_n)^T Z=(Z1,Z2,⋯,Zn)T则观测数据的似然函数为
P
(
Y
∣
θ
)
=
∑
Z
P
(
Z
∣
θ
)
P
(
Y
∣
Z
,
θ
)
(9.2)
P(Y|\theta) = \sum_Z P(Z|\theta) P(Y|Z,\theta) \tag{9.2}
P(Y∣θ)=Z∑P(Z∣θ)P(Y∣Z,θ)(9.2)
因为每次试验结果都是独立的,出现
Y
Y
Y的概率就可以写成每次试验概率连乘:
P
(
Y
∣
θ
)
=
∏
j
=
1
n
[
π
p
y
j
(
1
−
p
)
1
−
y
j
+
(
1
−
π
)
q
y
j
(
1
−
q
)
1
−
y
j
]
(9.3)
P(Y|\theta) = \prod_{j=1}^n [\pi p^{y_j}(1-p)^{1-y_j} +(1-\pi)q^{y_j}(1-q)^{1-y_j}] \tag{9.3}
P(Y∣θ)=j=1∏n[πpyj(1−p)1−yj+(1−π)qyj(1−q)1−yj](9.3)
考虑求模型参数
θ
=
(
π
,
p
,
q
)
\theta =(\pi,p,q)
θ=(π,p,q)的极大似然估计,即
θ
^
=
arg
max
θ
log
P
(
Y
∣
θ
)
(9.4)
\hat \theta = \arg\,\max_\theta \,\log P(Y|\theta) \tag{9.4}
θ^=argθmaxlogP(Y∣θ)(9.4)
就是求得使得式
(
9.3
)
(9.3)
(9.3)概率最大的参数
θ
\theta
θ。加了对数使连乘变成连加。
EM算法就是可以用于求解这个问题的一种迭代算法。下面给出针对以上问题的EM算法。
这里先给出EM算法的一个计算过程,其推导可见下文。
EM算法首先选取参数的初始值,记作
θ
(
0
)
=
(
π
(
0
)
,
p
(
0
)
,
q
(
0
)
)
\theta^{(0)}=(\pi^{(0)},p^{(0)},q^{(0)})
θ(0)=(π(0),p(0),q(0)),然后通过下面的步骤迭代计算参数的估计值,直到收敛为止。
所谓迭代,就是第 i + 1 i+1 i+1次的参数值可以通过第 i i i次来写出。第 i + 1 i+1 i+1次迭代过程如下:
- E步:计算在模型参数 π ( i ) , p ( i ) , q ( i ) \pi^{(i)},p^{(i)},q^{(i)} π(i),p(i),q(i)下观测数据 y j y_j yj来自掷硬币B的概率
μ j ( i + 1 ) = π ( i ) ( p ( i ) ) y j ( 1 − p ( i ) ) 1 − y j π ( i ) ( p ( i ) ) y j ( 1 − p ( i ) ) 1 − y j + ( 1 − π ( i ) ) ( q ( i ) ) y j ( 1 − q ( i ) ) 1 − y j (9.5) \mu_j^{(i+1)} = \frac{\pi^{(i)} (p^{(i)}) ^{y_j} (1-p^{(i)})^{1-y_j} }{\pi^{(i)} (p^{(i)}) ^{y_j} (1-p^{(i)})^{1-y_j} +(1- \pi^{(i)} )(q^{(i)}) ^{y_j} (1-q^{(i)})^{1-y_j} } \tag{9.5} μj(i+1)=π(i)(p(i))yj(1−p(i))1−yj+(1−π(i))(q(i))yj(1−q(i))1−yjπ(i)(p(i))yj(1−p(i))1−yj(9.5)
不要被这个式子吓到了,其实就是第 j j j份观测数据 y j y_j yj下,分母是公式 ( 9.1 ) (9.1) (9.1)的式子。
再啰嗦一下,上标 ( i ) (i) (i)表示第 i i i次迭代得到的参数值。而分子是来自硬币B的概率,根据 y j y_j yj的结果把正面和反面的式子写到了一起。再来看分母,分母就是来自硬币B的概率加上来自硬币C的概率。
- M步:计算模型参数的新估计量
π ( i + 1 ) = 1 n ∑ j = 1 n μ j ( i + 1 ) (9.6) \pi^{(i+1)} = \frac{1}{n} \sum_{j=1}^n \mu_j^{(i+1)} \tag{9.6} π(i+1)=n1j=1∑nμj(i+1)(9.6)
重点来了,我们说
π
\pi
π是硬币A正面朝上的概率,即得到的结果
y
y
y来自硬币B的概率,所以我们对E步计算出来的来自硬币B的概率求一个均值,就得到了更新后的
π
\pi
π。
p
(
i
+
1
)
=
∑
j
=
1
n
μ
j
(
i
+
1
)
y
j
∑
j
=
1
n
μ
j
(
i
+
1
)
(9.7)
p^{(i+1)} = \frac{ \sum_{j=1}^n \mu_j ^{(i+1)} y_j }{\sum_{j=1}^n \mu_j^{(i+1)} } \tag{9.7}
p(i+1)=∑j=1nμj(i+1)∑j=1nμj(i+1)yj(9.7)
结合面积图的话,就是计算深灰色区域。这里更新的是B正面朝上的概率。因为
y
∈
{
0
,
1
}
y \in \{0,1\}
y∈{0,1},所以可以这么写。B正面向上的概率除以B出现的总概率(加上B反面朝上的概率)。
q
(
i
+
1
)
=
∑
j
=
1
n
(
1
−
μ
j
(
i
+
1
)
)
y
j
∑
j
=
1
n
(
1
−
μ
j
(
i
+
1
)
)
(9.8)
q^{(i+1)} = \frac{ \sum_{j=1}^n (1-\mu_j ^{(i+1)} )y_j }{\sum_{j=1}^n (1-\mu_j^{(i+1)}) } \tag{9.8}
q(i+1)=∑j=1n(1−μj(i+1))∑j=1n(1−μj(i+1))yj(9.8)
这个就很容易理解了,
μ
\mu
μ是来自硬币B的概率,那么
(
1
−
μ
)
(1-\mu)
(1−μ)就是来自硬币C的概率。剩下的和公式
(
9.7
)
(9.7)
(9.7)类似。
下面通过程序来实现上面的公式,并赋予不同的初值,看得到的结果会怎样。
import numpy as np
Y = np.array([1,1,0,1,0,0,1,0,1,1])
pi,p,q = 0.5,0.5,0.5 #初始值,可变
count = 2 #简单实现,先固定迭代次数
pis,ps,qs = [pi],[p],[q] #保存历史计算结果
u = np.zeros(len(Y),dtype=np.float)
for c in range(count):
for i,y in enumerate(Y):
B = pis[c] * ps[c]**y * (1-ps[c])**(1-y)
C = (1-pis[c]) * qs[c]**y * (1-qs[c])**(1-y)
u[i] = B / (B +C)
pi = np.mean(u) #π
p = np.sum(u * Y) / np.sum(u)
q = np.sum((1-u) * Y) / np.sum(1-u)
pis.append(pi)
ps.append(p)
qs.append(q)
print('after iteration %d,pi=%2.4f,p=%2.4f,q=%2.4f' %(c+1,pi,p,q))
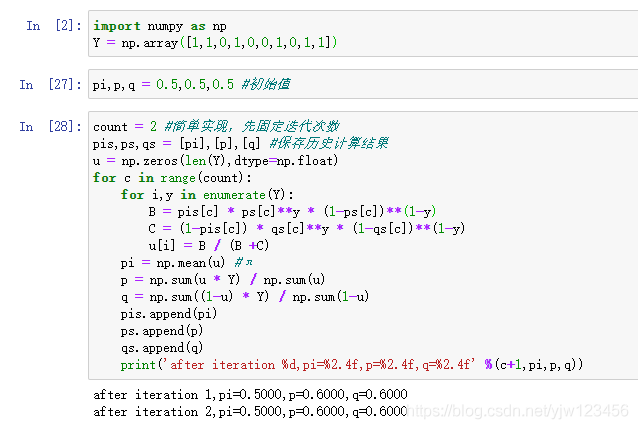
可以看到得到的结果和书上的是一样的。在给定不同的初始值,看得到的结果。
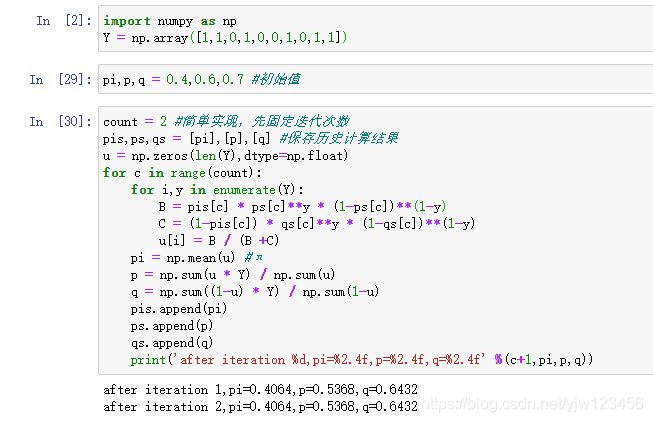
可以看到,EM算法与初值的选择有关,选择不同的初值可能得到不同的参数估计值。
一般地,用Y表示观测随机变量的数据,Z表示隐随机变量的数据。Y和Z连在一起成为完全数据,观测数据Y又称为不完全数据。假设给定观测数据Y,其概率分布是 P ( Y ∣ θ ) P(Y|\theta) P(Y∣θ),其中 θ \theta θ是需要估计的模型参数,那么不完全数据 Y Y Y的似然函数是 P ( Y ∣ θ ) P(Y|\theta) P(Y∣θ),对数似然函数 L ( θ ) = log P ( Y ∣ θ ) L(\theta) = \log P(Y|\theta) L(θ)=logP(Y∣θ);假设Y和Z的联合概率分布是 P ( Y , Z ∣ θ ) P(Y,Z|\theta) P(Y,Z∣θ),那么完全数据的对数似然函数是 log P ( Y , Z ∣ θ ) \log P(Y,Z|\theta) logP(Y,Z∣θ)。
EM算法通过迭代求 L ( θ ) = log P ( Y ∣ θ ) L(\theta) = \log P(Y|\theta) L(θ)=logP(Y∣θ)的极大似然顾及。每次迭代包含两步:E步,求期望;M步,求极大化。下面来介绍EM算法。
算法9.1 (EM算法)
输入:观测变量数据Y,隐变量数据Z,联合分布
P
(
Y
,
Z
∣
θ
)
P(Y,Z|\theta)
P(Y,Z∣θ),条件分布
P
(
Z
∣
Y
,
θ
)
P(Z|Y,\theta)
P(Z∣Y,θ);
输出:模型参数
θ
\theta
θ。
(1) 选择参数的初始值 θ ( 0 ) \theta^{(0)} θ(0),开始迭代;
(2) E步:记
θ
(
i
)
\theta^{(i)}
θ(i)为第
i
i
i次迭代参数
θ
\theta
θ的估计值,在第
i
+
1
i+1
i+1次迭代的E步,计算
Q
(
θ
,
θ
(
i
)
)
=
E
Z
[
log
P
(
Y
,
Z
∣
θ
)
∣
Y
,
θ
(
i
)
]
=
∑
Z
log
P
(
Y
,
Z
∣
θ
)
P
(
Z
∣
Y
,
θ
(
i
)
)
(9.9)
\begin{aligned} Q(\theta,\theta^{(i)}) &= E_Z[\log P(Y,Z|\theta)|Y,\theta^{(i)}] \\ &= \sum_Z \log P(Y,Z|\theta) P(Z|Y,\theta^{(i)}) \\ \end{aligned} \tag{9.9}
Q(θ,θ(i))=EZ[logP(Y,Z∣θ)∣Y,θ(i)]=Z∑logP(Y,Z∣θ)P(Z∣Y,θ(i))(9.9)
这里, P ( Z ∣ Y , θ ( i ) ) P(Z|Y,\theta^{(i)}) P(Z∣Y,θ(i))是在给定观测数据 Y Y Y和当前的参数估计 θ ( i ) \theta^{(i)} θ(i)下隐变量数据 Z Z Z的条件概率分布;
Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i))是条件分布 P ( Z ∣ Y , θ ( i ) ) P(Z|Y,\theta^{(i)}) P(Z∣Y,θ(i))下的期望。
(3) M步:求使
Q
(
θ
,
θ
(
i
)
)
Q(\theta,\theta^{(i)})
Q(θ,θ(i))极大化的
θ
\theta
θ,确定第
i
+
1
i+1
i+1次迭代的参数的估计值
θ
(
i
+
1
)
\theta^{(i+1)}
θ(i+1)
θ
(
i
+
1
)
=
arg
max
θ
Q
(
θ
,
θ
(
i
)
)
(9.10)
\theta^{(i+1)} = \arg \,\max _\theta Q(\theta,\theta^{(i)}) \tag{9.10}
θ(i+1)=argθmaxQ(θ,θ(i))(9.10)
(4) 重复第(2)步和第(3)步,直到收敛。
式
(
9.9
)
(9.9)
(9.9)的函数
Q
(
θ
,
θ
(
i
)
)
Q(\theta,\theta^{(i)})
Q(θ,θ(i))是EM算法的核心,称为
Q
Q
Q函数(Q function)。
定义 9.1(Q函数) 完全数据的对数似然函数
log
P
(
Y
,
Z
∣
θ
)
\log P(Y,Z|\theta)
logP(Y,Z∣θ)关于在给定观测数据
Y
Y
Y和当前参数
θ
(
i
)
\theta^{(i)}
θ(i)下对未观测数据
Z
Z
Z的条件概率分布
P
(
Z
∣
Y
,
θ
(
i
)
)
P(Z|Y,\theta^{(i)})
P(Z∣Y,θ(i))的期望称为
Q
Q
Q函数,即
Q
(
θ
,
θ
(
i
)
)
=
E
Z
[
log
P
(
Y
,
Z
∣
θ
)
∣
Y
,
θ
(
i
)
]
(9.11)
Q(\theta,\theta^{(i)}) = E_Z[\log P(Y,Z|\theta)|Y,\theta^{(i)}] \tag{9.11}
Q(θ,θ(i))=EZ[logP(Y,Z∣θ)∣Y,θ(i)](9.11)
对EM算法的几个步骤进行说明:
步骤(1) 参数的初值可以任意选择,但EM算法对初值是敏感的。
步骤(2) E步求 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i))。 Q Q Q函数式中 Z Z Z是未观测数据, Y Y Y是观测数据。 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i))中的第一个参数表示要极大化的参数,第二个参数是当前的估计值,即是一个确定的值。每次迭代实际在求 Q Q Q函数及其极大。
步骤(3) M步求 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i))的极大化,得到 θ ( i + 1 ) \theta^{(i+1)} θ(i+1),完成一次 θ ( i ) → θ ( i + 1 ) \theta^{(i)}\rightarrow \theta^{(i+1)} θ(i)→θ(i+1)的迭代。
步骤(4) 给出停止迭代的条件,一般是对较小的正数
ϵ
1
,
ϵ
2
\epsilon_1,\epsilon_2
ϵ1,ϵ2,若满足
∣
∣
θ
(
i
+
1
)
−
θ
(
i
)
∣
∣
≤
ϵ
1
或
∣
∣
Q
(
θ
(
i
+
1
)
,
θ
(
i
)
)
−
Q
(
θ
(
i
)
,
θ
(
i
)
)
∣
∣
≤
ϵ
2
||\theta^{(i+1)} - \theta^{(i)}|| \leq \epsilon_1 \quad \text{或} \quad ||Q(\theta^{(i+1)},\theta^{(i)}) - Q(\theta^{(i)},\theta^{(i)}) || \leq \epsilon_2
∣∣θ(i+1)−θ(i)∣∣≤ϵ1或∣∣Q(θ(i+1),θ(i))−Q(θ(i),θ(i))∣∣≤ϵ2
则停止迭代。
EM算法的导出
本节推导出式 ( 9.9 ) (9.9) (9.9)的 Q Q Q函数。
我们面对一个含有隐变量的概率模型,目标是极大化观测数据(不完全数据)
Y
Y
Y关于参数
θ
\theta
θ的对数似然函数,即极大化式
(
9.2
)
(9.2)
(9.2)的似然函数,取对数:
L
(
θ
)
=
log
P
(
Y
∣
θ
)
=
log
∑
Z
P
(
Z
∣
θ
)
P
(
Y
∣
Z
,
θ
)
(9.12)
L(\theta) = \log P(Y|\theta) = \log \sum_Z P(Z|\theta) P(Y|Z,\theta) \tag{9.12}
L(θ)=logP(Y∣θ)=logZ∑P(Z∣θ)P(Y∣Z,θ)(9.12)
这一极大化的主要难点在于其中包含未观测数据(
Z
Z
Z),并且包含和的对数
log
∑
\log \sum
log∑形式。
EM算法是通过迭代逐步近似极大化
L
(
θ
)
L(\theta)
L(θ)的。假设在第
i
i
i次迭代后
θ
\theta
θ的估计值是
θ
(
i
)
\theta^{(i)}
θ(i)。我们希望新估计值
θ
\theta
θ能使
L
(
θ
)
>
L
(
θ
(
i
)
)
L(\theta) > L(\theta^{(i)})
L(θ)>L(θ(i)),并逐步达到极大值。因此,可以考虑两者的差:
L
(
θ
)
−
L
(
θ
(
i
)
)
=
log
(
∑
Z
P
(
Y
∣
Z
,
θ
)
P
(
Z
∣
θ
)
)
−
log
P
(
Y
∣
θ
(
i
)
)
L(\theta) - L(\theta^{(i)}) = \log \left(\sum_Z P(Y|Z,\theta)P(Z|\theta) \right) - \log P(Y|\theta^{(i)})
L(θ)−L(θ(i))=log(Z∑P(Y∣Z,θ)P(Z∣θ))−logP(Y∣θ(i))
上式中的第二项 log P ( Y ∣ θ ( i ) ) \log P(Y|\theta^{(i)}) logP(Y∣θ(i))中的 Y Y Y和 θ ( i ) \theta^{(i)} θ(i)都是确定的值,因此不展开。根据我们上面补充知识中介绍的Jessen不等式,对上式中的 log ∑ \log \sum log∑转换为 ∑ log \sum \log ∑log的形式:
L
(
θ
)
−
L
(
θ
(
i
)
)
=
log
(
∑
Z
P
(
Y
∣
Z
,
θ
)
P
(
Z
∣
θ
)
)
−
log
P
(
Y
∣
θ
(
i
)
)
=
log
(
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
P
(
Z
∣
Y
,
θ
(
i
)
)
⋅
P
(
Y
∣
Z
,
θ
)
P
(
Z
∣
θ
)
)
−
log
P
(
Y
∣
θ
(
i
)
)
=
log
(
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
⋅
P
(
Y
∣
Z
,
θ
)
P
(
Z
∣
θ
)
P
(
Z
∣
Y
,
θ
(
i
)
)
)
−
log
P
(
Y
∣
θ
(
i
)
)
≥
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
log
P
(
Y
∣
Z
,
θ
)
P
(
Z
∣
θ
)
P
(
Z
∣
Y
,
θ
(
i
)
)
−
log
P
(
Y
∣
θ
(
i
)
)
=
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
log
P
(
Y
∣
Z
,
θ
)
P
(
Z
∣
θ
)
P
(
Z
∣
Y
,
θ
(
i
)
)
−
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
log
P
(
Y
∣
θ
(
i
)
)
... 因为
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
=
1
=
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
log
P
(
Y
∣
Z
,
θ
)
P
(
Z
∣
θ
)
P
(
Z
∣
Y
,
θ
(
i
)
)
P
(
Y
∣
θ
(
i
)
)
\begin{aligned} L(\theta) - L(\theta^{(i)}) &= \log \left(\sum_Z P(Y|Z,\theta)P(Z|\theta) \right) - \log P(Y|\theta^{(i)}) \\ &= \log \left(\sum_Z \frac{P(Z|Y,\theta^{(i)})}{P(Z|Y,\theta^{(i)})}\cdot P(Y|Z,\theta) P(Z|\theta)\right) -\log P(Y|\theta^{(i)}) \\ &= \log \left(\sum_Z P(Z|Y,\theta^{(i)}) \cdot \frac{P(Y|Z,\theta) P(Z|\theta)}{P(Z|Y,\theta^{(i)})}\right) -\log P(Y|\theta^{(i)}) \\ &\geq \sum_Z P(Z|Y,\theta^{(i)}) \log \frac{ P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})} - \log P(Y|\theta^{(i)}) \\ &= \sum_Z P(Z|Y,\theta^{(i)}) \log \frac{ P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})} - \sum_Z P(Z|Y,\theta^{(i)})\log P(Y|\theta^{(i)}) & \text{... 因为}\sum_Z P(Z|Y,\theta^{(i)})=1\\ &= \sum_Z P(Z|Y,\theta^{(i)}) \log \frac{ P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})P(Y|\theta^{(i)})} \end{aligned}
L(θ)−L(θ(i))=log(Z∑P(Y∣Z,θ)P(Z∣θ))−logP(Y∣θ(i))=log(Z∑P(Z∣Y,θ(i))P(Z∣Y,θ(i))⋅P(Y∣Z,θ)P(Z∣θ))−logP(Y∣θ(i))=log(Z∑P(Z∣Y,θ(i))⋅P(Z∣Y,θ(i))P(Y∣Z,θ)P(Z∣θ))−logP(Y∣θ(i))≥Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ(i))P(Y∣Z,θ)P(Z∣θ)−logP(Y∣θ(i))=Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ(i))P(Y∣Z,θ)P(Z∣θ)−Z∑P(Z∣Y,θ(i))logP(Y∣θ(i))=Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ(i))P(Y∣θ(i))P(Y∣Z,θ)P(Z∣θ)... 因为Z∑P(Z∣Y,θ(i))=1
这里引入
p
(
Z
∣
Y
,
θ
(
i
)
)
p(Z|Y,\theta^{(i)})
p(Z∣Y,θ(i)),给定
Y
,
θ
(
i
)
Y,\theta^{(i)}
Y,θ(i)下
Z
Z
Z的条件概率分布,也是一个概率分布,所以
∑
Z
p
(
Z
∣
Y
,
θ
(
i
)
)
=
1
\sum_Z p(Z|Y,\theta^{(i)}) =1
∑Zp(Z∣Y,θ(i))=1。符合Jesson不等式的要求。
令
B
(
θ
,
θ
(
i
)
)
=
^
L
(
θ
(
i
)
)
+
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
log
P
(
Y
∣
Z
,
θ
)
P
(
Z
∣
θ
)
P
(
Z
∣
Y
,
θ
(
i
)
)
P
(
Y
∣
θ
(
i
)
)
(9.13)
B(\theta,\theta^{(i)}) \hat{=} L(\theta^{(i)}) + \sum_Z P(Z|Y,\theta^{(i)}) \log \frac{ P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})P(Y|\theta^{(i)})} \tag{9.13}
B(θ,θ(i))=^L(θ(i))+Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ(i))P(Y∣θ(i))P(Y∣Z,θ)P(Z∣θ)(9.13)
相当于把前面的
L
(
θ
(
i
)
)
L(\theta^{(i)})
L(θ(i))移到等式右边,则
L
(
θ
)
≥
B
(
θ
,
θ
(
i
)
)
(9.14)
L(\theta) \geq B(\theta,\theta^{(i)}) \tag{9.14}
L(θ)≥B(θ,θ(i))(9.14)
这样就求得
L
(
θ
)
L(\theta)
L(θ)的一个下界,即
L
(
θ
)
L(\theta)
L(θ)最小值为
B
(
θ
,
θ
(
i
)
)
B(\theta,\theta^{(i)})
B(θ,θ(i))。将
θ
(
i
)
\theta^{(i)}
θ(i)代入式
(
9.13
)
(9.13)
(9.13),有
B
(
θ
(
i
)
,
θ
(
i
)
)
=
^
L
(
θ
(
i
)
)
+
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
log
P
(
Y
,
Z
∣
θ
(
i
)
)
P
(
Y
,
Z
∣
θ
(
i
)
)
=
L
(
θ
(
i
)
)
+
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
log
1
=
L
(
θ
(
i
)
)
B(\theta^{(i)},\theta^{(i)}) \hat{=} L(\theta^{(i)}) + \sum_Z P(Z|Y,\theta^{(i)}) \log \frac{ P(Y,Z|\theta^{(i)})}{P(Y,Z|\theta^{(i)})} = L(\theta^{(i)}) + \sum_Z P(Z|Y,\theta^{(i)}) \log 1= L(\theta^{(i)})
B(θ(i),θ(i))=^L(θ(i))+Z∑P(Z∣Y,θ(i))logP(Y,Z∣θ(i))P(Y,Z∣θ(i))=L(θ(i))+Z∑P(Z∣Y,θ(i))log1=L(θ(i))
即
L
(
θ
(
i
)
)
=
B
(
θ
(
i
)
,
θ
(
i
)
)
(9.15)
L(\theta^{(i)}) = B(\theta^{(i)},\theta^{(i)}) \tag{9.15}
L(θ(i))=B(θ(i),θ(i))(9.15)
说明
B
(
θ
,
θ
(
i
)
)
B(\theta,\theta^{(i)})
B(θ,θ(i))与
L
(
θ
)
L(\theta)
L(θ)在
θ
=
θ
(
i
)
\theta=\theta^{(i)}
θ=θ(i)处相交,
θ
(
i
)
\theta^{(i)}
θ(i)作为一个新的起点,任何可以使
B
(
θ
,
θ
(
i
)
)
B(\theta,\theta^{(i)})
B(θ,θ(i))增大的
θ
\theta
θ,也可以使
L
(
θ
)
L(\theta)
L(θ)增大。即为了
L
(
θ
)
L(\theta)
L(θ)尽可能大地增长,选择使
B
(
θ
,
θ
(
i
)
)
B(\theta,\theta^{(i)})
B(θ,θ(i))达到极大
θ
(
i
+
1
)
\theta^{(i+1)}
θ(i+1),即
θ
(
i
+
1
)
=
arg
max
θ
B
(
θ
,
θ
(
i
)
)
(9.16)
\theta^{(i+1)} =\arg\max_\theta B(\theta,\theta^{(i)}) \tag{9.16}
θ(i+1)=argθmaxB(θ,θ(i))(9.16)
现在求
θ
(
i
+
1
)
\theta^{(i+1)}
θ(i+1)的表达式,省去对
θ
\theta
θ极大化来说是常数的项,由式
(
9.16
)
(9.16)
(9.16)、
(
9.13
)
(9.13)
(9.13)及
(
9.10
)
(9.10)
(9.10)有
θ
(
i
+
1
)
=
arg
max
θ
(
L
(
θ
(
i
)
)
+
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
log
P
(
Y
∣
Z
,
θ
)
P
(
Z
∣
θ
)
P
(
Z
∣
Y
,
θ
(
i
)
)
P
(
Y
∣
θ
(
i
)
)
)
=
arg
max
θ
L
(
θ
(
i
)
)
⏟
L
(
θ
(
i
)
)
是常数
+
arg
max
θ
(
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
log
(
P
(
Y
∣
Z
,
θ
)
P
(
Z
∣
θ
)
)
)
−
arg
max
θ
(
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
log
(
P
(
Z
,
Y
∣
θ
(
i
)
)
)
)
⏟
Y
,
θ
(
i
)
已知,且对所有
Z
进行求和后也是常数
=
arg
max
θ
(
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
log
(
P
(
Y
∣
Z
,
θ
)
P
(
Z
∣
θ
)
)
)
=
arg
max
θ
(
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
log
P
(
Y
,
Z
∣
θ
)
)
=
arg
max
θ
Q
(
θ
,
θ
(
i
)
)
(9.17)
\begin{aligned} \theta^{(i+1)} &=\arg\max_\theta \left( L(\theta^{(i)}) + \sum_Z P(Z|Y,\theta^{(i)}) \log \frac{ P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})P(Y|\theta^{(i)})} \right) \\ &= \underbrace{\cancel{\arg\max_\theta L(\theta^{(i)})}}_{L(\theta^{(i)})是常数} + \arg\max_\theta \left( \sum_Z P(Z|Y,\theta^{(i)}) \log (P(Y|Z,\theta)P(Z|\theta)) \right) - \underbrace{\cancel{\arg\max_\theta \left(\sum_Z P(Z|Y,\theta^{(i)}) \log(P(Z,Y|\theta^{(i)})) \right)}}_{Y,\theta^{(i)}已知,且对所有Z进行求和后也是常数} \\ &= \arg\max_\theta \left( \sum_Z P(Z|Y,\theta^{(i)}) \log (P(Y|Z,\theta)P(Z|\theta)) \right) \\ &= \arg\max_\theta \left( \sum_Z P(Z|Y,\theta^{(i)}) \log P(Y,Z| \theta) \right) \\ &= \arg\max_\theta Q(\theta,\theta^{(i)}) \end{aligned} \tag{9.17}
θ(i+1)=argθmax(L(θ(i))+Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ(i))P(Y∣θ(i))P(Y∣Z,θ)P(Z∣θ))=L(θ(i))是常数
argθmaxL(θ(i))
+argθmax(Z∑P(Z∣Y,θ(i))log(P(Y∣Z,θ)P(Z∣θ)))−Y,θ(i)已知,且对所有Z进行求和后也是常数
argθmax(Z∑P(Z∣Y,θ(i))log(P(Z,Y∣θ(i))))
=argθmax(Z∑P(Z∣Y,θ(i))log(P(Y∣Z,θ)P(Z∣θ)))=argθmax(Z∑P(Z∣Y,θ(i))logP(Y,Z∣θ))=argθmaxQ(θ,θ(i))(9.17)
这就得到了
Q
Q
Q函数的表达式。上式等价于EM算法包含E步和M步的一次迭代,即求
Q
Q
Q函数及其极大化。
可以看到,EM算法是通过不断求解下界的极大化来逼近求解对数似然函数极大化的算法。
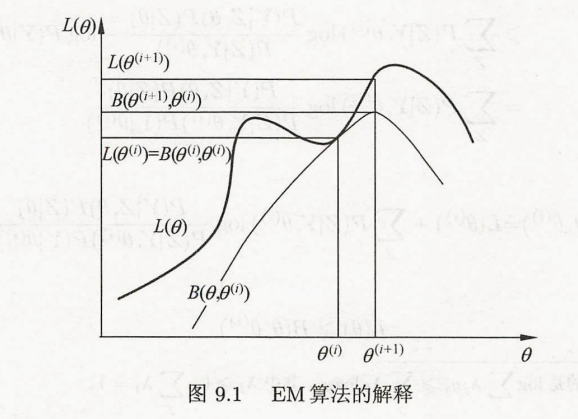
图9.1给出了EM算法的直观解释,来自原书。图中加粗上方曲线为 L ( θ ) L(\theta) L(θ),下方曲线为 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i))。 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i))为对数似然函数 L ( θ ) L(\theta) L(θ)的下界。由式 ( 9.15 ) (9.15) (9.15),两个函数在点 θ = θ ( i ) \theta=\theta^{(i)} θ=θ(i)处相等。EM算法找到下一个点 θ ( i + 1 ) \theta^{(i+1)} θ(i+1)使函数 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i))极大化,也是函数 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i))极大化。由于 L ( θ ) ≥ B ( θ , θ ( i ) ) L(\theta) \geq B(\theta,\theta^{(i)}) L(θ)≥B(θ,θ(i)),函数 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i))的增加,保证对数似然函数 L ( θ ) L(\theta) L(θ)在每次迭代中也是增加的。
EM算法在点 θ ( i + 1 ) \theta^{(i+1)} θ(i+1)处重新计算 Q Q Q函数值,进行下一次迭代。在此过程中,对数似然函数 L ( θ ) L(\theta) L(θ)不断增大,从图可以看出EM算法不能保证找到全局最优值。
EM算法的收敛性
EM算法提供一种近似计算含有隐变量概率模型的极大似然估计的方法。那么EM算法得到的估计序列是否收敛?下面给出EM算法收敛性的两个定理。
定理 9.1 设
P
(
Y
∣
θ
)
P(Y|\theta)
P(Y∣θ)为观测数据的似然函数,
θ
(
i
)
(
i
=
1
,
2
,
⋯
)
\theta^{(i)}(i=1,2,\cdots)
θ(i)(i=1,2,⋯)为EM算法得到的参数估计序列,
P
(
Y
∣
θ
(
i
)
)
(
i
=
1
,
2
,
⋯
)
P(Y|\theta^{(i)})(i=1,2,\cdots)
P(Y∣θ(i))(i=1,2,⋯)为对应的似然函数序列,则
P
(
Y
∣
θ
(
i
)
)
P(Y|\theta^{(i)})
P(Y∣θ(i))是单调递增的,即
P
(
Y
∣
θ
(
i
+
1
)
)
≥
P
(
Y
∣
θ
(
i
)
)
(9.18)
P(Y|\theta^{(i+1)}) \geq P(Y|\theta^{(i)}) \tag{9.18}
P(Y∣θ(i+1))≥P(Y∣θ(i))(9.18)
证明 由于
P
(
Y
∣
θ
)
=
P
(
Y
,
Z
∣
θ
)
P
(
Z
∣
Y
,
θ
)
P(Y|\theta) = \frac{P(Y,Z|\theta)}{P(Z|Y,\theta)}
P(Y∣θ)=P(Z∣Y,θ)P(Y,Z∣θ)
取对数有
log
P
(
Y
∣
θ
)
=
log
P
(
Y
,
Z
∣
θ
)
−
log
P
(
Z
∣
Y
,
θ
)
\log P(Y|\theta) = \log P(Y,Z|\theta) - \log P(Z|Y,\theta)
logP(Y∣θ)=logP(Y,Z∣θ)−logP(Z∣Y,θ)
上述等式两边在条件分布
P
(
Z
∣
Y
,
θ
(
i
)
)
P(Z|Y,\theta^{(i)})
P(Z∣Y,θ(i))下求期望,得:
E
Z
∣
Y
,
θ
(
i
)
[
log
P
(
Y
∣
θ
)
]
=
E
Z
∣
Y
,
θ
(
i
)
[
log
P
(
Y
,
Z
∣
θ
)
−
log
P
(
Z
∣
Y
,
θ
)
]
E_{Z|Y,\theta^{(i)}} [\log P(Y|\theta) ] = E_{Z|Y,\theta^{(i)}}[\log P(Y,Z|\theta) - \log P(Z|Y,\theta)]
EZ∣Y,θ(i)[logP(Y∣θ)]=EZ∣Y,θ(i)[logP(Y,Z∣θ)−logP(Z∣Y,θ)]
等式左边有:
E
Z
∣
Y
,
θ
(
i
)
[
log
P
(
Y
∣
θ
)
]
=
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
log
P
(
Y
∣
θ
)
=
log
P
(
Y
∣
θ
)
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
=
log
P
(
Y
∣
θ
)
\begin{aligned} E_{Z|Y,\theta^{(i)}} [\log P(Y|\theta) ] &= \sum_Z P(Z|Y,\theta^{(i)}) \log P(Y|\theta) \\ &= \log P(Y|\theta) \sum_Z P(Z|Y,\theta^{(i)}) \\ &= \log P(Y|\theta) \end{aligned}
EZ∣Y,θ(i)[logP(Y∣θ)]=Z∑P(Z∣Y,θ(i))logP(Y∣θ)=logP(Y∣θ)Z∑P(Z∣Y,θ(i))=logP(Y∣θ)
等式右边有:
E
Z
∣
Y
,
θ
(
i
)
[
log
P
(
Y
,
Z
∣
θ
)
−
log
P
(
Z
∣
Y
,
θ
)
]
=
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
log
P
(
Y
,
Z
∣
θ
)
−
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
log
P
(
Z
∣
Y
,
θ
)
E_{Z|Y,\theta^{(i)}}[\log P(Y,Z|\theta) - \log P(Z|Y,\theta)] = \sum_Z P(Z|Y,\theta^{(i)}) \log P(Y,Z|\theta) - \sum_Z P(Z|Y,\theta^{(i)}) \log P(Z|Y,\theta)
EZ∣Y,θ(i)[logP(Y,Z∣θ)−logP(Z∣Y,θ)]=Z∑P(Z∣Y,θ(i))logP(Y,Z∣θ)−Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ)
由式
(
9.11
)
(9.11)
(9.11)
Q
(
θ
,
θ
(
i
)
)
=
∑
Z
log
P
(
Y
,
Z
∣
θ
)
P
(
Z
∣
Y
,
θ
(
i
)
)
Q(\theta,\theta^{(i)}) = \sum_Z \log P(Y,Z|\theta) P(Z|Y,\theta^{(i)})
Q(θ,θ(i))=Z∑logP(Y,Z∣θ)P(Z∣Y,θ(i))
可知上述等式右边第一项就是
Q
(
θ
,
θ
(
i
)
)
Q(\theta,\theta^{(i)})
Q(θ,θ(i))。
令
H
(
θ
,
θ
(
i
)
)
=
∑
Z
log
P
(
Z
∣
Y
,
θ
)
P
(
Z
∣
Y
,
θ
(
i
)
)
(9.19)
H(\theta,\theta^{(i)}) = \sum_Z \log P(Z|Y,\theta) P(Z|Y,\theta^{(i)}) \tag{9.19}
H(θ,θ(i))=Z∑logP(Z∣Y,θ)P(Z∣Y,θ(i))(9.19)
上述等式左边等于右边,于是对数似然函数可以写成
log
P
(
Y
∣
θ
)
=
Q
(
θ
,
θ
(
i
)
)
−
H
(
θ
,
θ
(
i
)
)
(9.20)
\log P(Y|\theta) =Q(\theta,\theta^{(i)}) - H(\theta,\theta^{(i)}) \tag{9.20}
logP(Y∣θ)=Q(θ,θ(i))−H(θ,θ(i))(9.20)
为了证明式
(
9.18
)
(9.18)
(9.18),在式
(
9.20
)
(9.20)
(9.20)中分别取
θ
\theta
θ为
θ
(
i
+
1
)
\theta^{(i+1)}
θ(i+1)和
θ
(
i
)
\theta^{(i)}
θ(i)并相减,有
log
P
(
Y
∣
θ
(
i
+
1
)
)
−
log
P
(
Y
∣
θ
(
i
)
)
=
Q
(
θ
(
i
+
1
)
,
θ
(
i
)
)
−
H
(
θ
(
i
+
1
)
,
θ
(
i
)
)
−
[
Q
(
θ
(
i
)
,
θ
(
i
)
)
−
H
(
θ
(
i
)
,
θ
(
i
)
)
]
=
[
Q
(
θ
(
i
+
1
)
,
θ
(
i
)
)
−
Q
(
θ
(
i
)
,
θ
(
i
)
)
]
−
[
H
(
θ
(
i
+
1
)
,
θ
(
i
)
)
−
H
(
θ
(
i
)
,
θ
(
i
)
)
]
(9.21)
\begin{aligned} \log P &(Y|\theta^{(i+1)}) - \log P(Y|\theta^{(i)}) \\ &= Q(\theta^{(i+1)},\theta^{(i)}) - H(\theta^{(i+1)},\theta^{(i)}) - [Q(\theta^{(i)},\theta^{(i)}) - H(\theta^{(i)},\theta^{(i)})]\\ &= [Q(\theta^{(i+1)},\theta^{(i)}) - Q(\theta^{(i)},\theta^{(i)})] - [H(\theta^{(i+1)},\theta^{(i)}) - H(\theta^{(i)},\theta^{(i)})] \end{aligned} \tag{9.21}
logP(Y∣θ(i+1))−logP(Y∣θ(i))=Q(θ(i+1),θ(i))−H(θ(i+1),θ(i))−[Q(θ(i),θ(i))−H(θ(i),θ(i))]=[Q(θ(i+1),θ(i))−Q(θ(i),θ(i))]−[H(θ(i+1),θ(i))−H(θ(i),θ(i))](9.21)
我们只要证明式
(
9.21
)
(9.21)
(9.21)两端是非负的,就能。式
(
9.21
)
(9.21)
(9.21)右端的第1项,由于
θ
(
i
+
1
)
\theta^{(i+1)}
θ(i+1)使
Q
(
θ
,
θ
(
i
)
)
Q(\theta,\theta^{(i)})
Q(θ,θ(i))达到极大,所以有
Q
(
θ
(
i
+
1
)
,
θ
(
i
)
)
−
Q
(
θ
(
i
)
,
θ
(
i
)
)
≥
0
(9.22)
Q(\theta^{(i+1)},\theta^{(i)}) - Q(\theta^{(i)},\theta^{(i)}) \geq 0 \tag{9.22}
Q(θ(i+1),θ(i))−Q(θ(i),θ(i))≥0(9.22)
其第2项,由式
(
9.19
)
(9.19)
(9.19)可得:
H
(
θ
(
i
+
1
)
,
θ
(
i
)
)
−
H
(
θ
(
i
)
,
θ
(
i
)
)
=
∑
Z
log
P
(
Z
∣
Y
,
θ
(
i
+
1
)
)
P
(
Z
∣
Y
,
θ
(
i
)
)
−
∑
Z
log
P
(
Z
∣
Y
,
θ
(
i
)
)
P
(
Z
∣
Y
,
θ
(
i
)
)
=
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
(
log
P
(
Z
∣
Y
,
θ
(
i
+
1
)
)
P
(
Z
∣
Y
,
θ
(
i
)
)
)
≤
log
(
∑
Z
P
(
Z
∣
Y
,
θ
(
i
)
)
⋅
P
(
Z
∣
Y
,
θ
(
i
+
1
)
)
P
(
Z
∣
Y
,
θ
(
i
)
)
)
=
log
(
∑
Z
P
(
Z
∣
Y
,
θ
(
i
+
1
)
)
=
log
1
=
0
(9.23)
\begin{aligned} H(\theta^{(i+1)},\theta^{(i)}) - H(\theta^{(i)},\theta^{(i)}) &= \sum_Z \log P(Z|Y,\theta^{(i+1)}) P(Z|Y,\theta^{(i)}) -\sum_Z \log P(Z|Y,\theta^{(i)}) P(Z|Y,\theta^{(i)}) \\ &= \sum_Z P(Z|Y,\theta^{(i)}) \left(\log \frac{P(Z|Y,\theta^{(i+1)})}{ P(Z|Y,\theta^{(i)})} \right) \\ &\leq \log \left( \sum_Z P(Z|Y,\theta^{(i)}) \cdot \frac{P(Z|Y,\theta^{(i+1)})}{ P(Z|Y,\theta^{(i)})} \right) \\ &= \log \left( \sum_Z P(Z|Y,\theta^{(i+1)} \right) \\ &= \log 1 \\ &= 0 \end{aligned} \tag{9.23}
H(θ(i+1),θ(i))−H(θ(i),θ(i))=Z∑logP(Z∣Y,θ(i+1))P(Z∣Y,θ(i))−Z∑logP(Z∣Y,θ(i))P(Z∣Y,θ(i))=Z∑P(Z∣Y,θ(i))(logP(Z∣Y,θ(i))P(Z∣Y,θ(i+1)))≤log(Z∑P(Z∣Y,θ(i))⋅P(Z∣Y,θ(i))P(Z∣Y,θ(i+1)))=log(Z∑P(Z∣Y,θ(i+1))=log1=0(9.23)
这里再次利用了Jessen不等式,由式
(
9.22
)
(9.22)
(9.22)和式
(
9.23
)
(9.23)
(9.23)可知式
(
9.21
)
(9.21)
(9.21)右端是非负的。
定理 9.2 设 L ( θ ) = log P ( Y ∣ θ ) L(\theta)=\log P(Y|\theta) L(θ)=logP(Y∣θ)为观测数据的对数似然函数, θ ( i ) ( i = 1 , 2 , ⋯ ) \theta^{(i)}(i=1,2,\cdots) θ(i)(i=1,2,⋯)为EM算法得到的参数估计序列, L ( θ ( i ) ) ( i = 1 , 2 ⋯ ) L(\theta^{(i)})(i=1,2\cdots) L(θ(i))(i=1,2⋯)为对应的对数似然函数序列。
(1) 如果 P ( Y ∣ θ ) P(Y|\theta) P(Y∣θ)有上界,则 L ( θ ( i ) ) = log P ( Y ∣ θ ( i ) ) L(\theta^{(i)})=\log P(Y|\theta^{(i)}) L(θ(i))=logP(Y∣θ(i))收敛到某一值 L ∗ L^* L∗;
(2) 在函数 Q ( θ , θ ′ ) Q(\theta,\theta^\prime) Q(θ,θ′)与 L ( θ ) L(\theta) L(θ)满足一定条件下,由EM算法得到的参数估计序列 θ ( i ) \theta^{(i)} θ(i)的收敛值 θ ∗ \theta^* θ∗是 L ( θ ) L(\theta) L(θ)的稳定点。