作者简介:大家好,我是未央;
博客首页:未央.303
系列专栏:Java初阶数据结构
每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!!
文章目录
前言
一、向上调整来建堆
二、向下调整来建堆
三、向上建堆和向下建堆的优劣比较
总结
前言
上节内容我们介绍了优先级队列的实现方法,即通过向上调整和向下调整算法实现创建大根堆或者小根堆。本节内容我们将比较这两种算法,找出其优劣;

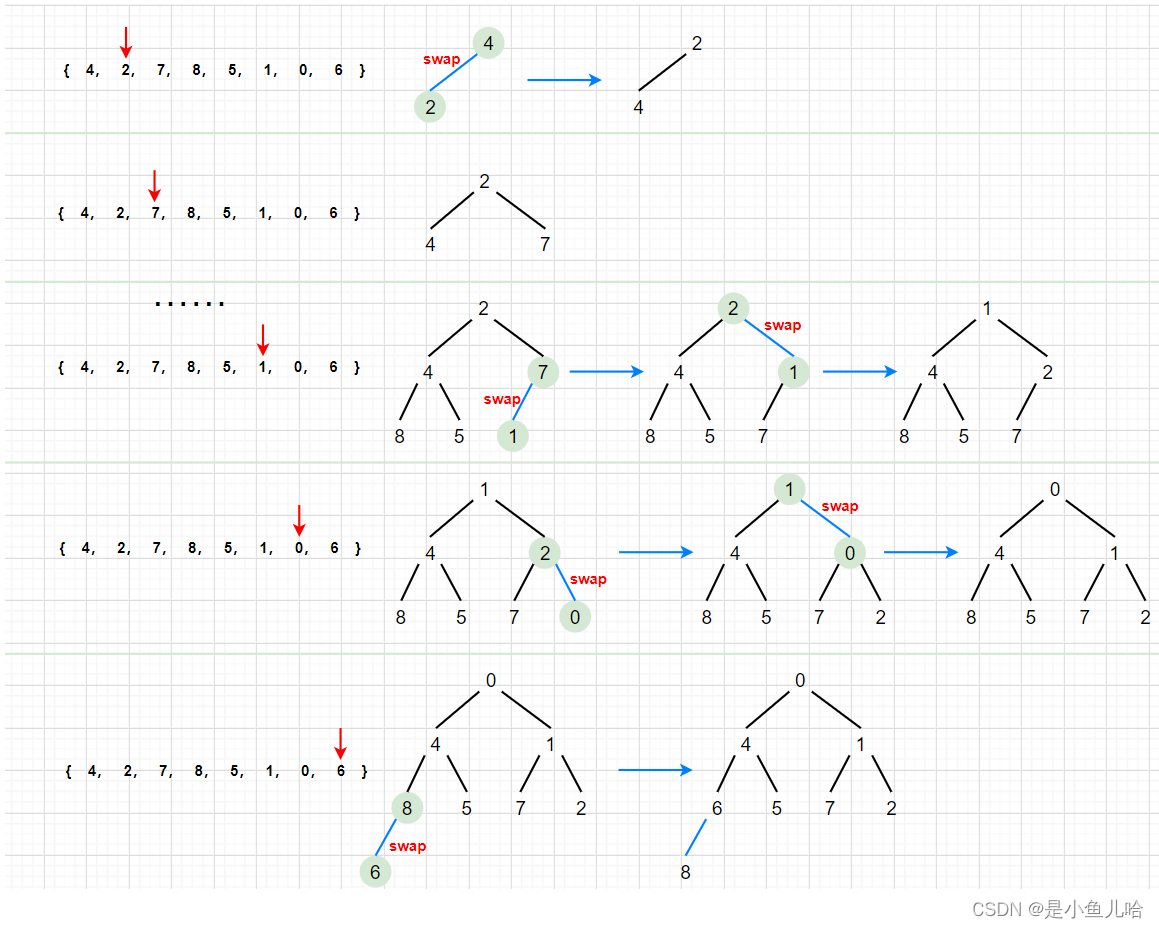
我们先举例对于这样一个数组来建立一个小根堆;

一、向上调整来建堆
思想:
首先,我们把第一个数字看成堆,也就是4,当第二个数字插入进去的时候,进行向上调整算法,使其确保为小堆;(向上调整的算法在上篇博文已详细讲解过,不过多赘述)
一个一个的插入数据的过程就是遍历数组,确保数组里每一个数进行向上调整算法;
其过程的图解:
代码实现:
????????????????具体时间
public class Test2 {
private int[] array;
private int usedSize; // 当前堆中的有效元素个数
Test2() {
array = new int[10]; // 通过构造方法给数组分配空间
}
// 向上调整保证是小根堆:时间复杂度是O(log以2为底的N)---log2N
public void shiftUp(int child) {
int parent = (child - 1) / 2;
while (parent >= 0) {
if (this.array[child] < this.array[parent]) {
int tmp = this.array[child];
this.array[child] = array[parent];
this.array[parent] = tmp;
child = parent;
parent = (child - 1) / 2;
}
else {
break;
}
}
}
// 向堆中插入元素
public void offerHeap(int val) {
if (this.usedSize >= this.array.length) {
System.out.println("数组已满,插入失败!");
}
else {
this.array[usedSize] = val;
shiftUp(usedSize); // 插入数据后进行向上调整确保为小堆
++usedSize; // 堆中有效元素加一个
}
}
// 向上调整建立小根堆,时间复杂度是O(n * log2N)
public void createHeapUp() {
int[] a = {4, 2, 7, 8, 5, 1, 0, 6};
// 遍历a数组,将a数组中的元素一个一个的插入堆中
for (int i = 0; i < a.length; i++) {
offerHeap(a[i]);
}
}
public static void main(String[] args) {
Test2 test2 = new Test2();
test2.createHeapUp();
}
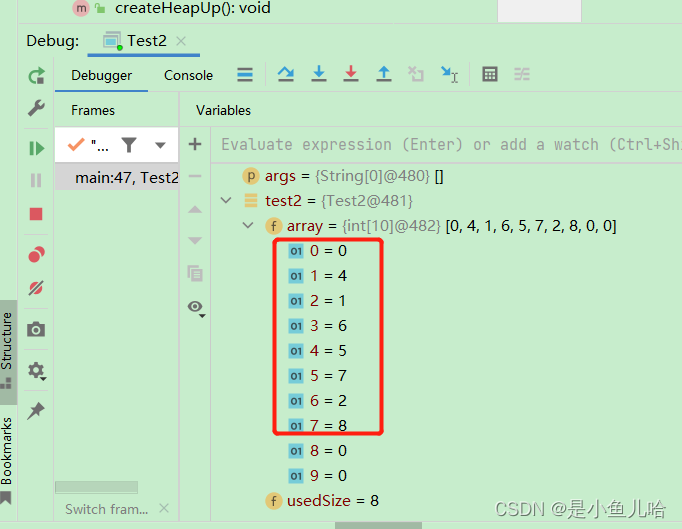
}运行结果:
上面我们是一个一个的插入来建立小根堆的,那么我们能不能直接把数组看作是一个堆,然后对数组中的元素进行向上调整——建立小根堆呢?
当然是可以的;
代码示例:
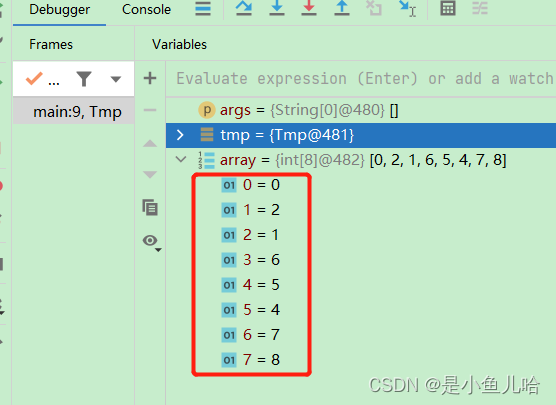
import java.util.Arrays; // 向上调整建立小根堆 public class Main { public static void main(String[] args) { Main tmp = new Main(); int[] array = {4, 2, 7, 8, 5, 1, 0, 6}; //int[] array = {4, 1, 3, 2, 0}; tmp.createHeapUp2(array); System.out.println(Arrays.toString(array)); } // 向上调整保证是小根堆:时间复杂度是O(log以2为底的N)---log2N public void shiftUp(int[] array, int child) { int parent = (child - 1) / 2; while (parent >= 0) { if (array[child] < array[parent]) { int tmp = array[child]; array[child] = array[parent]; array[parent] = tmp; child = parent; parent = (child - 1) / 2; } else { break; } } } // 建立小根堆的方法二: // 向上调整建立小根堆,时间复杂度是O(n * log2N) public void createHeapUp2(int[] array) { for (int i = 1; i < array.length; ++i) { shiftUp(array, i); // 对数组的每一个元素进行向上调整 } } // 我们向下调整来建堆时,要保证当前要调整的节点的左右子树都已经是堆后,才可以向下调整。 // 向上调整来建立堆的时候,也是相似的,要保证要调整的节点前面已经是一个合法的堆才行—— // 为了达到这个目的,我们在向上建堆的时候,就需要从数组的第二个元素开始(也可以理解为第二层的第一个节点) }运行结果:
注意:
这个建堆的结果可能和向下调整来建堆一样,但思想其实是不同的;
二、向下调整来建堆
根据该数组建立小根堆
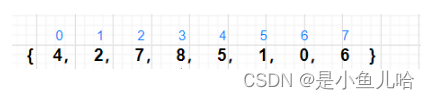
思路:
因为向下调整的前提是根结点的左右子树均为小堆或大堆才可,而这里,数组为乱序的,无法直接从根结点开始向下调整;
所以我们从倒数第一个非叶结点开始向下调整,从下往上调:
思路分析:
从该解决方案中,我们首先要找到这个倒数第一个非叶结点的数在哪?其实最后一个结点的父亲即为倒数第一个非叶结点。当我们找到这个非叶结点时,把它和它的孩子看成一个整体,进行向下调整。调整后,再将次父节点向前挪动,再次向下调整,依次循环下去。
再回顾下父亲和孩子间的关系:
- leftchild = parent*2 + 1;
- rightchild = parent*2 + 2;
- parent = (child - 1) / 2;
分析过程的图解 :
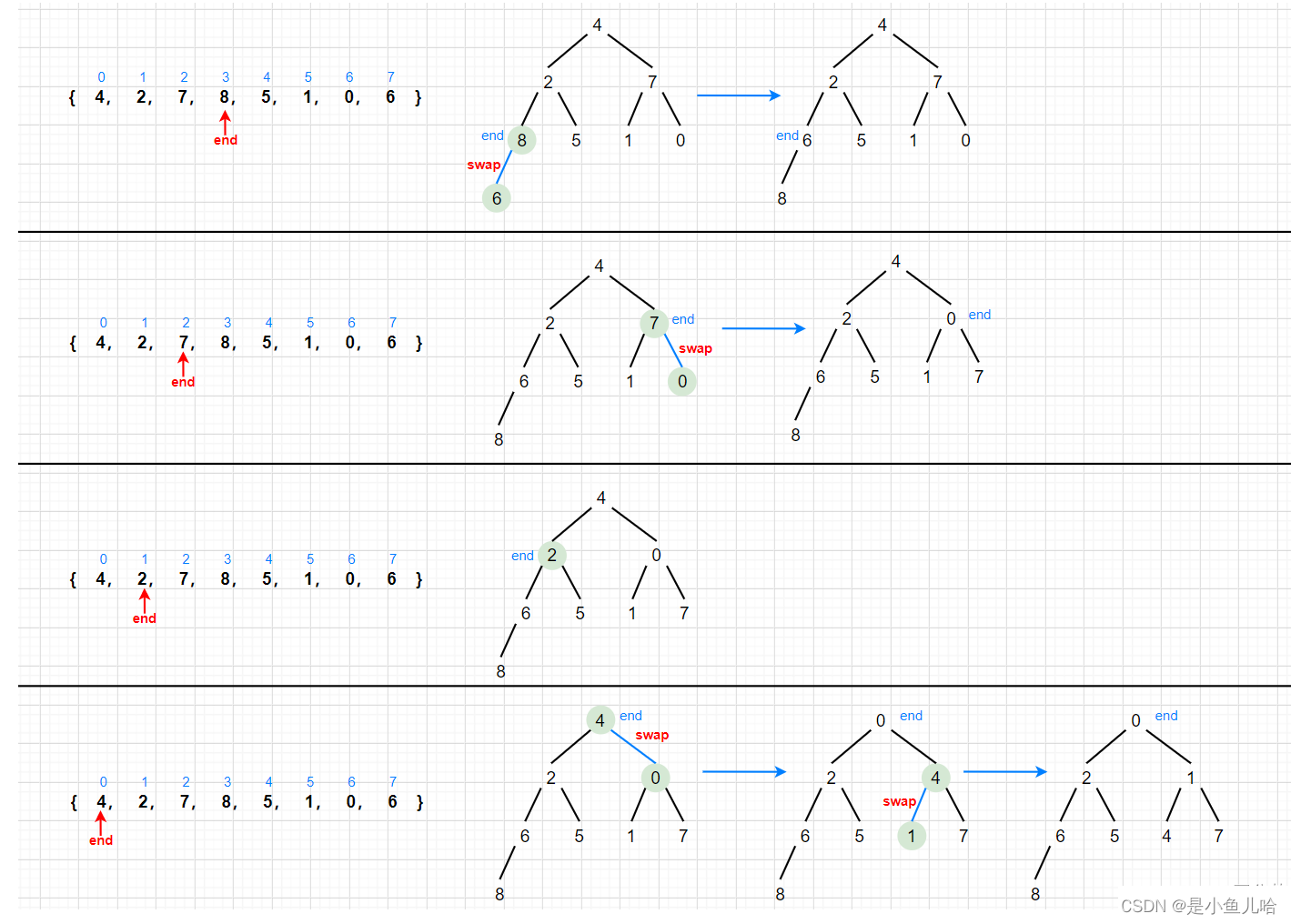
代码实现:
import java.util.Arrays; public class Test3 { public void createHeap(int[] arrays) { // 从倒数的第一个非叶子节点开始调节(调节他的左右子树),一直调节到根结点(根节点在数组中的下标为0) // 注意这里是usdSize - 1 - 1,因为父亲结点的下标 = (孩子结点的下标 - 1) / 2, // 我们是从倒数的第一个非叶子节点的子树开始调节的,而该子树的孩子结点坐标为arrays.length - 1 for (int i = (arrays.length - 1 - 1) / 2; i >= 0 ; --i) { shiftDown(arrays, i); // 从下面的子树一直调到上面的子树 } } /** * 向下调整——使得当前子树为小根堆 * @param root 是每棵子树的根结点的下标 * 向下调整的时间复杂度O(log2n)(最坏情况下就是树的高度) */ public void shiftDown(int[] arrays, int root) { int parent = root; // 父亲结点的坐标 int child = 2 * parent + 1; // 获取左孩子结点的坐标 // 为什么不能child下标要小于usedSize,因为当前数组的最大下标就是usedSize - 1,如果大于或等于usedSize就越界了 while (child < arrays.length) { // 每个子树在调整的时候,是按从上到下,当child的下标小于usedSize时候就结束 // 这一步目的是找出孩子结点最小的那个值,然后在让该值和父亲结点比较(不过先要确定孩子结点存在) if (child + 1 < arrays.length - 1 && arrays[child] > arrays[child + 1]) { child = child + 1; } if (arrays[child] < arrays[parent]) { int tmp = arrays[child]; arrays[child] = arrays[parent]; arrays[parent] = tmp; parent = child; // 从上向下调整子树,更新父亲结点的下标 child = 2 * parent + 1; // 更新左孩子孩子结点的下标 } // 因为我们是从上向下调整子树,当我们在调整上面的子树时,下面的子树一定是调整好了的,如果上面都已经满足小根堆,下面也一定满足 else { break; // 此时已经是小根堆了,不需要再次调整,直接退出循环接着调整下一个子树 } } } public static void main(String[] args) { Test3 test3 = new Test3(); int[] a = {4, 2, 7, 8, 5, 1, 0, 6}; test3.createHeap(a); // 注意我们建立的小根堆没有储存在a数组中,而是储存在Test3类中的elem数组中 System.out.println(Arrays.toString(a)); } }运行结果:
同上面向上调整算法一致;
总结:
1.向下调整来建堆时,要保证当前要调整的节点的左右子树都已经是堆后,才可以向下调整。所以我们要从倒数第一个非叶子结点开始调整
2.向上调整来建立堆的时候,也是相似的,要保证要调整的节点前面已经是一个合法的堆才行——为了达到这个目的,我们在向上建堆的时候,就需要从数组的第二个元素开始(也可以理解为第二层的第一个节点)

三、向上建堆和向下建堆的优劣比较
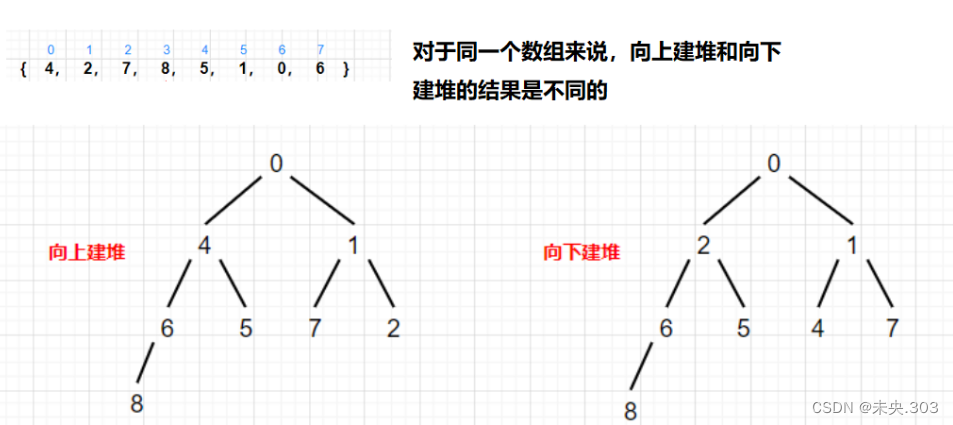
我们看一下他们各自的时间复杂度 :
举例说明:
有一棵满完全二叉树:
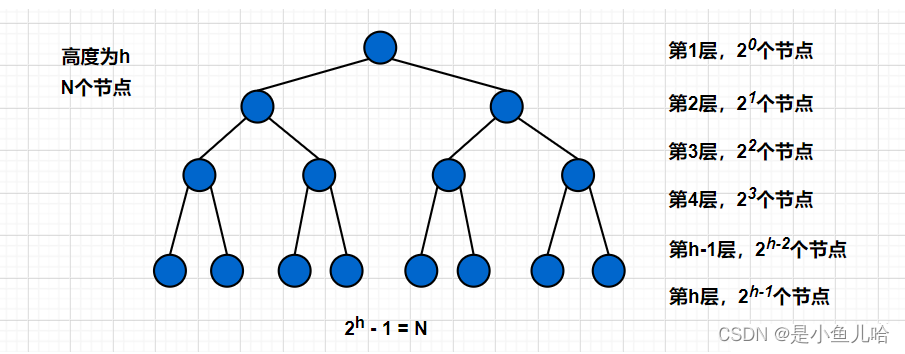
对于向上建堆计算:
思路分析:
时间复杂度计算的是其调整的次数,根据上文的知识我们已经知晓其是从数组的第二个元素开始的,也就是可以理解为第二层的第一个节点。计算的思想非常简单:计算每层有多少个节点乘以该层的高度次,然后累计相加即可;
如下:
通过计算得知:向上建堆的时间复杂度为O(N*logN);
对于向下建堆计算:
思路分析:
向下调整我们前面已经知道它是从倒数第1个非叶节点开始调整的;
每层的调整次数为:该层的节点个数*该层高度减1;
一直从倒数第2层开始调直至第1层,并将其依次累加,累加的计算过程和向上调整差不多,都是等比*等差的求和;(但不同的是:每层的调整次数不同)
如下:
通过计算得知:向下建堆的时间复杂度为O(n);
综上,向下建堆其实性能更好一定;
总结


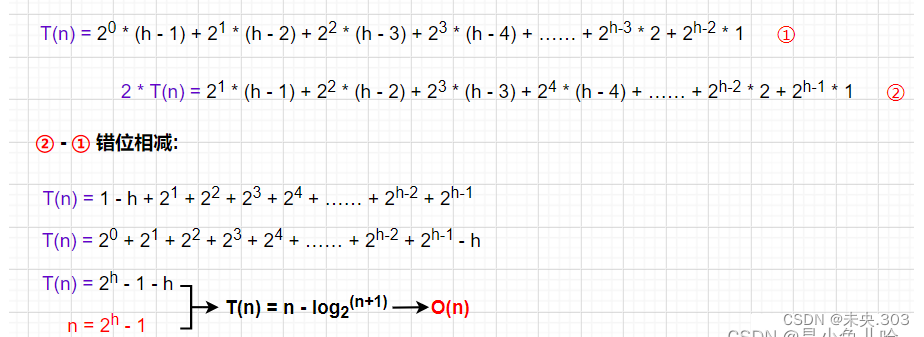










![用友T3提示,年度[UFDATA_002_2017]并不存在,导致无法备份迁移。](https://img-blog.csdnimg.cn/8cd3df4697534eb2bf5c26d15aa45b70.png#pic_center)