Key Points
1D变2D
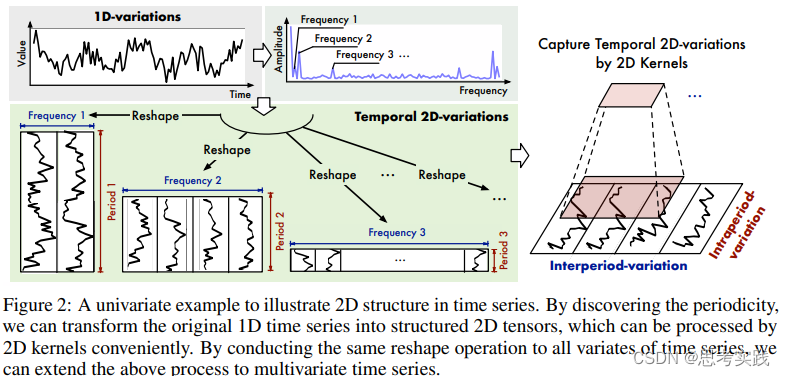
这是本文的核心。大部分现有方法都是作用于时间序列的时间维度,捕获时序依赖性。实际上,现实时间序列一般都有多种模式,比如不同的周期,各种趋势,这些模式混杂在一起。如果直接对原始序列的时间维度来建模,真正的时序关系很可能隐藏在这些混杂的模式中,无法被捕获。考虑到:现实世界的时间序列通常具有多周期性,比如每天周期、每周周期、每月周期;而且,每个周期内部的时间点是有依赖关系的(比如今天1点和2点),不同的相邻周期内的时间点也是有依赖关系的(比如今天1点和明天1点),作者提出将1D的时间维度reshape成2D的,示意图如下。下图左侧的时间序列具有三个比较显著的周期性(Period 1、Period 2、Period 3),将其reshape成三种不同的2D-variations,2D-variations的每一列包含一个时间段(周期)内的时间点,每一行包含不同时间段(周期)内同一阶段的时间点。变成2D-variations之后,就可以采用2D卷积等方式来同时捕获时间段内部依赖和相邻时间段依赖。

为了确定时间序列中的周期性,可以使用傅里叶变换来分析其频率成分。通过对时间序列进行傅里叶变换后,可以得到不同频率的复数值,并且主要周期对应的频率成分通常具有高振幅,即高幅值。因此,可以选择取最大的k个幅值对应的频率成分来确定top k个主要的周期。类似于Autoformer中的处理方式。
具体操作如下图所示。首先,从所有频率成分中选择top k个幅值最大的成分,以此确定top k个主要周期。在此只画了三个周期作为示例。然后,将原始1D时间序列reshape成三种不同的2D形式(如果不能整除,则可以使用padding),并对这三种2D形式的序列分别采用2D卷积进行处理,最后聚合处理结果即可得到时间序列的周期性特征。
需要注意的是,在实际应用中,可能需要根据具体问题对top k的值进行调整,并对选取的周期进行更深入的分析。
这一步需要看代码搞懂具体怎么变换的。
为了直观理解2D变化,我们在图9中展示了转换后的2D张量。根据可视化结果,我们可以得到以下观察结果:
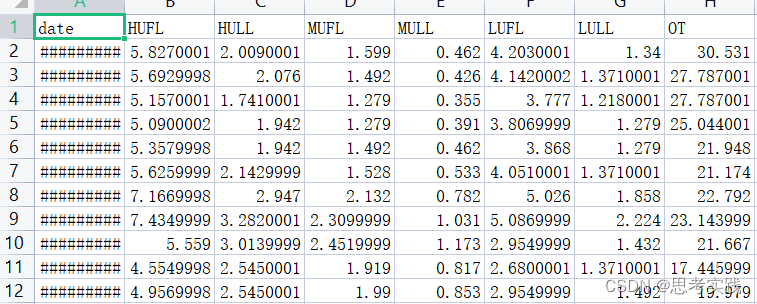
• 交替周期变化能够呈现时间序列的长期趋势。例如,在Exchange数据集的第一个例子中,每行的值从左到右递减,表明原始序列的下降趋势。而对于ETTh1数据集,每行的值相互类似,反映了原始序列的全局稳定变化。(这个ETTh1这个的说法我不太完全赞同,因为数据集Exchange与ETTh1分别如图所示,ETTh1怎么会稳定呢?)
Exchange:

ETTh1:
• 对于没有明显周期性的时间序列,时间上的2D变化仍然可以呈现有用的2D结构。如果频率为一,则交替周期变化就是原始序列的变化。此外,交替周期变化也可以呈现长期趋势,有益于时间变化建模。
• 转换后的2D变化展示了两种类型的局部性。首先,对于每一列(周期内变化),相邻的值彼此接近,呈现出相邻时间点之间的局部性。其次,对于每一行(交替周期变化),相邻的值也很接近,对应于相邻周期之间的局部性。请注意,非相邻周期之间可能差异很大,这可能是由于全局趋势造成的,例如来自Exchange数据集的情况。这些局部性的观察结果也激发了我们采用2D卷积进行表示学习的想法。

模型代码:Time-Series-Library/TimesNet.py at main · thuml/Time-Series-Library · GitHub
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.fft
from layers.Embed import DataEmbedding
from layers.Conv_Blocks import Inception_Block_V1
def FFT_for_Period(x, k=2):
# [B, T, C]
xf = torch.fft.rfft(x, dim=1)
# find period by amplitudes
frequency_list = abs(xf).mean(0).mean(-1)
'''
这行代码计算了每个频率成分在所有时间步和通道上的平均幅值,返回一个长度为T/2+1的tensor。具
体地,首先使用abs函数计算xf的绝对值,然后在dim=0上取平均值(即对所有样本取平均),再在
dim=-1上取平均值(即对所有通道取平均)。结果是一个形状为[T/2+1]的tensor,其中第一个元素代
表直流成分,即对应于0 Hz的频率成分。
'''
frequency_list[0] = 0
_, top_list = torch.topk(frequency_list, k)
top_list = top_list.detach().cpu().numpy()
period = x.shape[1] // top_list
return period, abs(xf).mean(-1)[:, top_list]
'''
这段代码使用FFT来找出时间序列中的主要周期,并返回top k个周期对应的幅值。
输入参数x是一个形状为[B, T, C]的tensor,分别表示batch size、时间步和通道数。
在该函数中,通过使用torch.fft.rfft来进行实数快速傅里叶变换,得到频域复数张量xf [B, T/2+1, C]。
然后,计算各个频率成分的平均幅值,将第一个元素设为0(代表直流成分),并使用torch.topk函数找到前k个最大幅值对应的频率成分(即top k个周期)。
对于每个找到的周期,计算其在时间轴上的长度(即时间步数)并返回周期列表。
同时,选择top k个周期对应的频率成分,并返回它们在每个样本通道上的幅值。
'''
class TimesBlock(nn.Module):
def __init__(self, configs):
super(TimesBlock, self).__init__()
self.seq_len = configs.seq_len
self.pred_len = configs.pred_len
self.k = configs.top_k
# parameter-efficient design
self.conv = nn.Sequential(
Inception_Block_V1(configs.d_model, configs.d_ff,
num_kernels=configs.num_kernels),
nn.GELU(),
Inception_Block_V1(configs.d_ff, configs.d_model,
num_kernels=configs.num_kernels)
)
def forward(self, x):
B, T, N = x.size()
period_list, period_weight = FFT_for_Period(x, self.k)
res = []
for i in range(self.k):
period = period_list[i]
# padding
if (self.seq_len + self.pred_len) % period != 0:
length = (
((self.seq_len + self.pred_len) // period) + 1) * period
padding = torch.zeros([x.shape[0], (length - (self.seq_len + self.pred_len)), x.shape[2]]).to(x.device)
out = torch.cat([x, padding], dim=1)
else:
length = (self.seq_len + self.pred_len)
out = x
# reshape
out = out.reshape(B, length // period, period,
N).permute(0, 3, 1, 2).contiguous()
# 2D conv: from 1d Variation to 2d Variation
out = self.conv(out)
# reshape back
out = out.permute(0, 2, 3, 1).reshape(B, -1, N)
res.append(out[:, :(self.seq_len + self.pred_len), :])
res = torch.stack(res, dim=-1)
# adaptive aggregation
period_weight = F.softmax(period_weight, dim=1)
period_weight = period_weight.unsqueeze(
1).unsqueeze(1).repeat(1, T, N, 1)
res = torch.sum(res * period_weight, -1)
# residual connection
res = res + x
return res
class Model(nn.Module):
"""
Paper link: https://openreview.net/pdf?id=ju_Uqw384Oq
"""
def __init__(self, configs):
super(Model, self).__init__()
self.configs = configs
self.task_name = configs.task_name
self.seq_len = configs.seq_len
self.label_len = configs.label_len
self.pred_len = configs.pred_len
self.model = nn.ModuleList([TimesBlock(configs)
for _ in range(configs.e_layers)])
self.enc_embedding = DataEmbedding(configs.enc_in, configs.d_model, configs.embed, configs.freq,
configs.dropout)
self.layer = configs.e_layers
self.layer_norm = nn.LayerNorm(configs.d_model)
if self.task_name == 'long_term_forecast' or self.task_name == 'short_term_forecast':
self.predict_linear = nn.Linear(
self.seq_len, self.pred_len + self.seq_len)
self.projection = nn.Linear(
configs.d_model, configs.c_out, bias=True)
if self.task_name == 'imputation' or self.task_name == 'anomaly_detection':
self.projection = nn.Linear(
configs.d_model, configs.c_out, bias=True)
if self.task_name == 'classification':
self.act = F.gelu
self.dropout = nn.Dropout(configs.dropout)
self.projection = nn.Linear(
configs.d_model * configs.seq_len, configs.num_class)
def forecast(self, x_enc, x_mark_enc, x_dec, x_mark_dec):
# Normalization from Non-stationary Transformer
means = x_enc.mean(1, keepdim=True).detach()
x_enc = x_enc - means
stdev = torch.sqrt(
torch.var(x_enc, dim=1, keepdim=True, unbiased=False) + 1e-5)
x_enc /= stdev
# embedding
enc_out = self.enc_embedding(x_enc, x_mark_enc) # [B,T,C]
enc_out = self.predict_linear(enc_out.permute(0, 2, 1)).permute(
0, 2, 1) # align temporal dimension
# TimesNet
for i in range(self.layer):
enc_out = self.layer_norm(self.model[i](enc_out))
# porject back
dec_out = self.projection(enc_out)
# De-Normalization from Non-stationary Transformer
dec_out = dec_out * \
(stdev[:, 0, :].unsqueeze(1).repeat(
1, self.pred_len + self.seq_len, 1))
dec_out = dec_out + \
(means[:, 0, :].unsqueeze(1).repeat(
1, self.pred_len + self.seq_len, 1))
return dec_out
def imputation(self, x_enc, x_mark_enc, x_dec, x_mark_dec, mask):
# Normalization from Non-stationary Transformer
means = torch.sum(x_enc, dim=1) / torch.sum(mask == 1, dim=1)
means = means.unsqueeze(1).detach()
x_enc = x_enc - means
x_enc = x_enc.masked_fill(mask == 0, 0)
stdev = torch.sqrt(torch.sum(x_enc * x_enc, dim=1) /
torch.sum(mask == 1, dim=1) + 1e-5)
stdev = stdev.unsqueeze(1).detach()
x_enc /= stdev
# embedding
enc_out = self.enc_embedding(x_enc, x_mark_enc) # [B,T,C]
# TimesNet
for i in range(self.layer):
enc_out = self.layer_norm(self.model[i](enc_out))
# porject back
dec_out = self.projection(enc_out)
# De-Normalization from Non-stationary Transformer
dec_out = dec_out * \
(stdev[:, 0, :].unsqueeze(1).repeat(
1, self.pred_len + self.seq_len, 1))
dec_out = dec_out + \
(means[:, 0, :].unsqueeze(1).repeat(
1, self.pred_len + self.seq_len, 1))
return dec_out
def anomaly_detection(self, x_enc):
# Normalization from Non-stationary Transformer
means = x_enc.mean(1, keepdim=True).detach()
x_enc = x_enc - means
stdev = torch.sqrt(
torch.var(x_enc, dim=1, keepdim=True, unbiased=False) + 1e-5)
x_enc /= stdev
# embedding
enc_out = self.enc_embedding(x_enc, None) # [B,T,C]
# TimesNet
for i in range(self.layer):
enc_out = self.layer_norm(self.model[i](enc_out))
# porject back
dec_out = self.projection(enc_out)
# De-Normalization from Non-stationary Transformer
dec_out = dec_out * \
(stdev[:, 0, :].unsqueeze(1).repeat(
1, self.pred_len + self.seq_len, 1))
dec_out = dec_out + \
(means[:, 0, :].unsqueeze(1).repeat(
1, self.pred_len + self.seq_len, 1))
return dec_out
def classification(self, x_enc, x_mark_enc):
# embedding
enc_out = self.enc_embedding(x_enc, None) # [B,T,C]
# TimesNet
for i in range(self.layer):
enc_out = self.layer_norm(self.model[i](enc_out))
# Output
# the output transformer encoder/decoder embeddings don't include non-linearity
output = self.act(enc_out)
output = self.dropout(output)
# zero-out padding embeddings
output = output * x_mark_enc.unsqueeze(-1)
# (batch_size, seq_length * d_model)
output = output.reshape(output.shape[0], -1)
output = self.projection(output) # (batch_size, num_classes)
return output
def forward(self, x_enc, x_mark_enc, x_dec, x_mark_dec, mask=None):
if self.task_name == 'long_term_forecast' or self.task_name == 'short_term_forecast':
dec_out = self.forecast(x_enc, x_mark_enc, x_dec, x_mark_dec)
return dec_out[:, -self.pred_len:, :] # [B, L, D]
if self.task_name == 'imputation':
dec_out = self.imputation(
x_enc, x_mark_enc, x_dec, x_mark_dec, mask)
return dec_out # [B, L, D]
if self.task_name == 'anomaly_detection':
dec_out = self.anomaly_detection(x_enc)
return dec_out # [B, L, D]
if self.task_name == 'classification':
dec_out = self.classification(x_enc, x_mark_enc)
return dec_out # [B, N]
return None这位同学解读的代码也可以
(291条消息) TimesNet 代码阅读_刘泓君的博客-CSDN博客
参考资料
(2023 ICLR)TimesNet:Temporal 2D-Variation Modeling for General Time Series Analysis - 知乎 (zhihu.com)
ICLR 2023 |任务通用的时序分析骨干网络TimesNet - 知乎 (zhihu.com)









![用友T3提示,年度[UFDATA_002_2017]并不存在,导致无法备份迁移。](https://img-blog.csdnimg.cn/8cd3df4697534eb2bf5c26d15aa45b70.png#pic_center)