343. 整数拆分
思路:
-
确定dp数组(dp table)以及下标的含义:dp[i]:分拆数字i,可以得到的最大乘积为dp[i]。
-
确定递推公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j))
可以想 dp[i]最大乘积是怎么得到的呢?
其实可以从1遍历j,然后有两种渠道得到dp[i].
一个是j * (i - j) 直接相乘。
一个是j * dp[i - j],相当于是拆分(i - j)。
-
dp数组如何初始化:dp[0] dp[1] 不应该初始化,没有意义的数值。dp[2] = 1
-
确定遍历顺序:dp[0] dp[1] 就不应该初始化,也就是没有意义的数值。
-
举例推导dp数组
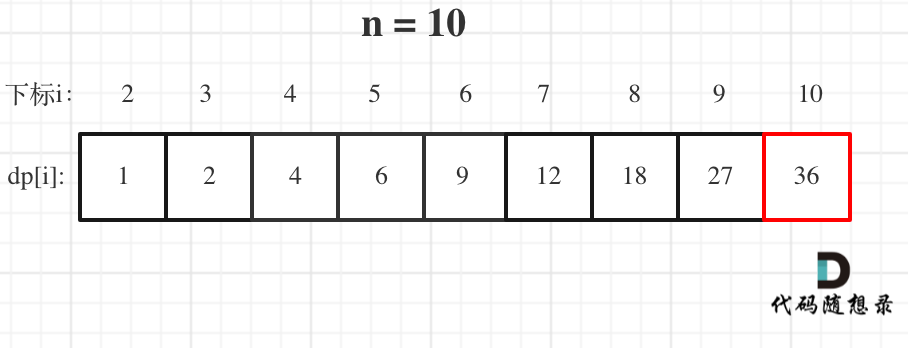
举例当n为10 的时候,dp数组里的数值,如下:
class Solution:
def integerBreak(self, n: int) -> int:
dp = [0] *(n+1)
dp[2] = 1
# 假设对正整数 i 拆分出的第一个正整数是 j(1 <= j < i),则有以下两种方案:
# 1) 将 i 拆分成 j 和 i−j 的和,且 i−j 不再拆分成多个正整数,此时的乘积是 j * (i-j)
# 2) 将 i 拆分成 j 和 i−j 的和,且 i−j 继续拆分成多个正整数,此时的乘积是 j * dp[i-j]
for i in range(3,n+1):
for j in range(1,i):
dp[i] = max(dp[i],j*(i-j),j*dp[i-j])
return dp[n]
96.不同的二叉搜索树
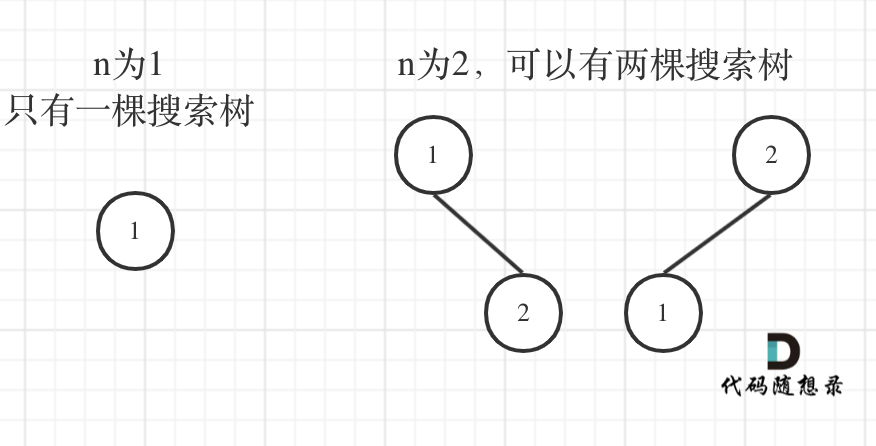
n为1的时候有一棵树,n为2有两棵树,这个是很直观的。
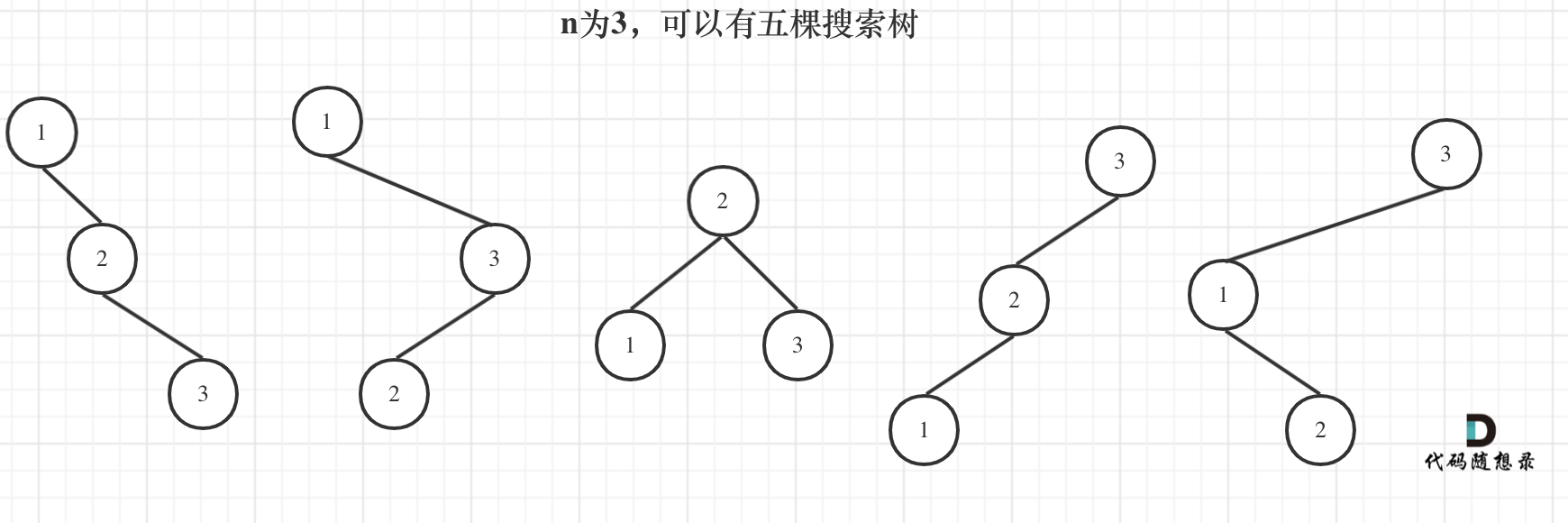
可以通过dp[1] 和 dp[2] 来推导出来dp[3]的某种方式。
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
如图所示: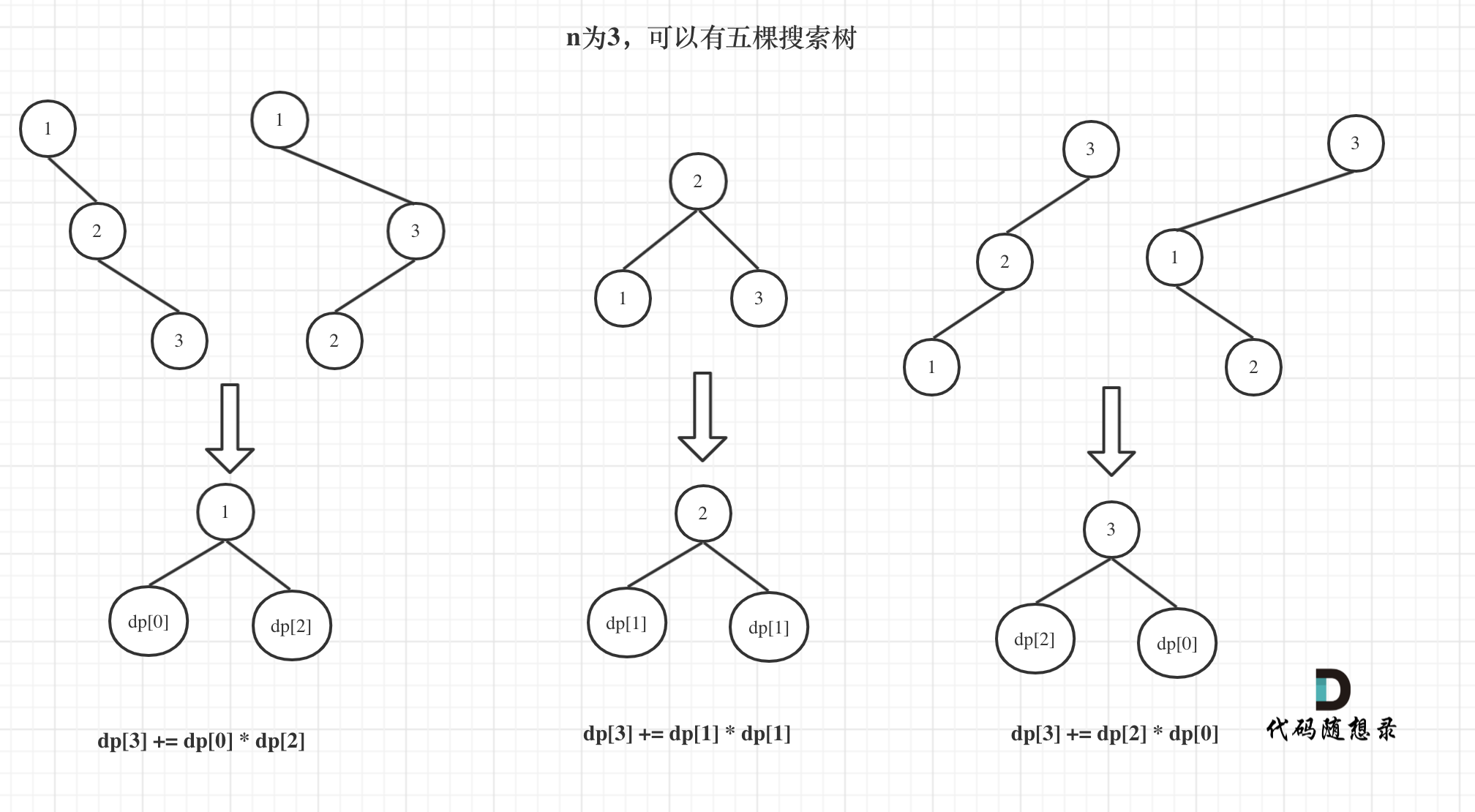
思路 :
-
确定dp数组(dp table)以及下标的含义:dp[i] : 1到i为节点组成的二叉搜索树的个数为dp[i]。
-
确定递推公式:dp[i] += dp[j - 1] * dp[i - j]
dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
-
dp数组如何初始化:dp[0] = 1
-
确定遍历顺序:遍历i里面每一个数作为头结点的状态,用j来遍历
-
举例推导dp数组
n为5时候的dp数组状态如图:
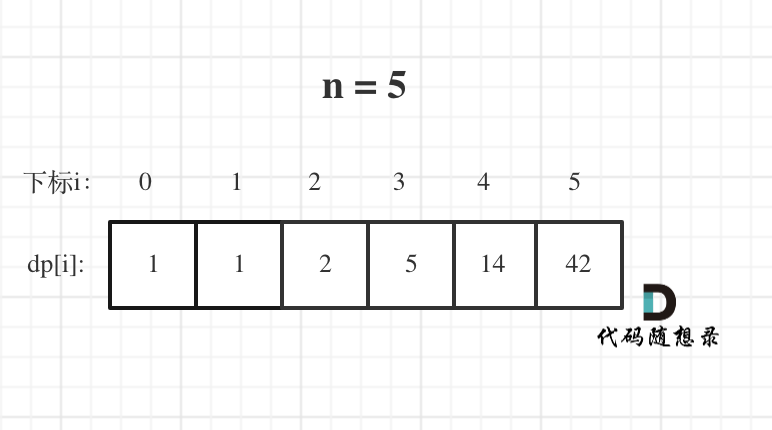
class Solution:
def numTrees(self, n: int) -> int:
dp = [0 for _ in range(n+1)]
dp[0] = 1
for i in range(1,n+1):
for j in range(1,i+1):
dp[i] += dp[j-1]*dp[i-j]
return dp[n]










![用友T3提示,年度[UFDATA_002_2017]并不存在,导致无法备份迁移。](https://img-blog.csdnimg.cn/8cd3df4697534eb2bf5c26d15aa45b70.png#pic_center)