田昌源. 基于自适应事件触发控制的一般线性多智能体系统的一致性[D].青岛大学,2022.DOI:10.27262/d.cnki.gqdau.2022.002546.

第五章 一般线性多智能体系统的自适应事件触发二分一致性

5.1 系统模型

第 $i$ 个智能体的动态方程为为

$$\begin{array}{rl}{\dot{x}}_i& =A{x}_i(t)+B{u}_i(t)\end{array}\text{\hspace{1em}(5-1)}$$

领导者为

$$\begin{array}{rl}{\dot{x}}_0& =A{x}_0(t)\end{array}\text{\hspace{1em}(5-2)}$$

5.2 自适应事件触发二分一致性

5.2.1 无领导一致性

在本节中，基于无领导的多智能体系统 (5-1)，提出如下分布式自适应事件触发二分一致性协议

$$\begin{array}{r}{u}_i(t)=K{c}_i(t)\sum _{j\in N_i}{a}_{ij}(x_j(t_k^i)-\text{sgn}(a_{ij})x_i(t_k^i))\end{array}\text{\hspace{1em}(5-3)}$$

$$\begin{array}{rl}{\dot{c}}_t(t)& =[\sum _{j\in N_i}{a}_{ij}(x_j(t_k^i)-\text{sgn}(a_{ij})x_i(t_k^i)){]}^{\text{T}}\Gamma [\sum _{j\in N_i}{a}_{ij}(x_j(t_k^i)-\text{sgn}(a_{ij})x_i(t_k^i))]\end{array}\text{\hspace{1em}(5-4)}$$

其中
$t_k^i$ 表示智能体 $i$ 的第 $k$ 个事件触发时刻且 $t_0^i=0$，
$K\in {\mathbb{R}}^{m\times n}$ 和 $\Gamma \in {\mathbb{R}}^{m\times n}$ 是反馈增益矩阵，
$c_i(t)$ 表示节点 $i$ 的时变耦合权值且 $c_i(0)>0$。

---

对每一个智能体，引入辅助变量 ${\eta }_i(t)$，设计如下动态事件触发函数

η ˙ i ( t ) = − ρ i η i ( t ) + v i { 1 4 ∑ j ∈ N i a i j ( x ~ i ( t ) − x ~ j ( t ) ) T Γ ( ( x ~ i ( t ) − x ~ j ( t ) ) − ∑ j ∈ N i ( 1 + σ c i j ( t ) ) a i j e i T Γ e i ( t ) } (4-7) \begin{aligned} \dot{\eta}_i(t) &= - \rho_i \eta_i(t) + v_i \{ \frac{1}{4} \sum_{j\in N_i} a_{ij} (\tilde{x}_i(t) - \tilde{x}_j(t) )^\text{T} \Gamma ((\tilde{x}_i(t) - \tilde{x}_j(t)) \\ & - \sum_{j \in N_i} (1 + \sigma c_{ij}(t)) a_{ij} e_i^\text{T} \Gamma e_i(t) \} \end{aligned} \tag{4-7} η˙​i​(t)​=−ρi​ηi​(t)+vi​{41​j∈Ni​∑​aij​(x~i​(t)−x~j​(t))TΓ((x~i​(t)−x~j​(t))−j∈Ni​∑​(1+σcij​(t))aij​eiT​Γei​(t)}​(4-7)

---

定义智能体的状态估计为
$${\tilde{x}}_i(t)={\text{e}}^{A(t-t_k^i)}{x}_i(t_k^i)$$

智能体的状态误差定义为
$$e_i(t)={\tilde{x}}_i(t)-x_i(t)$$

---

$$\begin{array}{r}\end{array}\text{\hspace{1em}(5-11)}$$

5.2.2 领导-跟随一致性

5.3 数值仿真

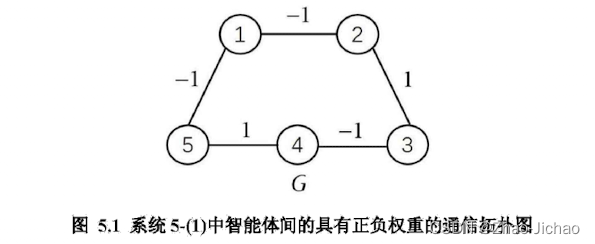
程序名字 main_couplingWeight_ETC.m，效果如下：

完全按照论文的描述出不来效果，针对原文有改动。

Ref

---

需要程序代码可加+V：Zhao-Jichao