本文编辑:调皮哥的小助理
上文从FMCW毫米波雷达系统的性能参数理解4D成像毫米波雷达的设计思路,谈到关于设计4D毫米波成像雷达的思路,其实我还忽略了一点,在这里补充说明一下。
在文中谈到的最小化公式中,分母的有效带宽其实可以通过跳频技术来增加,并采用相参合成方式提高距离分辨率,从而实现高距离分辨率。这里的核心技术是跳频,而步进调频连续波是其中的一种特例。
好了,今天主要分享从奈奎斯特采样定理推导FMCW雷达系统性能参数。
1、最大不模糊距离
距离维度,也被称为快时间维,其采样率满足如下关系:
f s ≥ 2 f I F − max (实采样 ) f s ≥ f I F − max ( 复采样 ) \begin{gathered}\left.f_s \geq 2 f_{I F-\max } \text { (实采样 }\right) \\ f_s \geq f_{I F-\max }(\text { 复采样 })\end{gathered} fs≥2fIF−max (实采样 )fs≥fIF−max( 复采样 )
如果不满足上述条件,就会出现距离维度的混叠,也就是距离模糊。采样定理的本质是频谱搬移,如下图中红色交叉部分,混叠部分的频谱将会体现在距离维FFT后的距离门上,使得雷达距离估计出现错误。

因此,最大不模糊距离公式为:
R max = c f s 2 S R_{\max }=\frac{c f_s}{2 S} Rmax=2Scfs
如果采样率满足采样定理,那么最大不模糊距离(最大探测距离)就由FMCW的最大中频带宽决定,如果不满足采样定理,则最大不模糊距离就由 上述公式决定。也就是说采样率不够,频谱搬移没有完全搬出去,剩下的红色部分交叉在尾部的频带上产生了混叠。
一般来说,雷达都是满足采样定理的,这里只是想到了这个话题,就随便说了几句。
2、最大不模糊速度
同理,雷达对目标的速度采样也要满足采样定理,否则会在速度维度,也被称为快时间维产生混叠,也就是速度模糊。
一般来说,雷达并不知道目标的运动速度是多少,因此雷达工程师必须要设置一个边界,比如最大探测速度是100Km/h。如果目标的速度超过这个边界值,则会出现模糊,意思就是超过了雷达的对速度的采样,会出现混叠。
其实我主要关心的是下面这个公式,即 4 π v T c λ < π \frac{4 \pi v T_{\mathrm{c}}}{\lambda}<\pi λ4πvTc<π ,为什么成立?
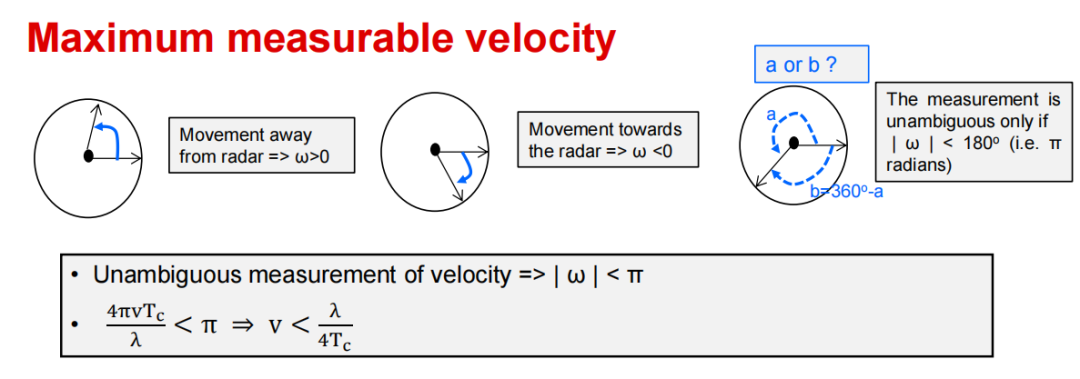
用几何的方式可以理解,即角频率超过180°后出现了相位模糊,但是我想从公式角度推导一下。
其实,无论我们如何设计雷达的波形参数,雷达检测目标的速度是有限的,不可能无穷大。因此,雷达的最大不模糊速度是有界的,即存在收敛。
因此,我们设计雷达系统时设计好PRT后,对速度的采样率就固定不变了,可以用下列公式表达:
f s = 1 T c f_s=\frac{1}{T_c} fs=Tc1
其中,Tc是Chirp的间隔时间,也就是PRT。采样后的信号的最高频率等于信号的采样率,我们可以先假定当前已经满足了采样定理,即:
f s ≥ 2 f f_s \geq 2 f fs≥2f
然后根据目前这个参数,去求解最大不模糊速度即可,最后再推导出 4 π v T C λ < π \frac{4 \pi v \mathrm{~T}_{\mathrm{C}}}{\lambda}<\pi λ4πv TC<π 的结论。
f是多普勒频率,其实雷达对目标运动速度的采样本质上就是对多普勒频率进行采样,故:
f s ≥ 2 f = 2 ( 2 v λ ) f_s \geq 2 f=2\left(\frac{2 v}{\lambda}\right) fs≥2f=2(λ2v)
而 v = λ ω 4 π T c v=\frac{\lambda \omega}{4 \pi T_c} v=4πTcλω ,则可以得到:
f s = 1 T c ≥ 2 f = 2 ( 2 λ ω 4 π T c λ ) f_s=\frac{1}{T_c} \geq 2 f=2\left(\frac{2 \frac{\lambda \omega}{4 \pi T_c}}{\lambda}\right) fs=Tc1≥2f=2(λ24πTcλω)
最终得到 ∣ ω ∣ < π |\omega|<\pi ∣ω∣<π ,即得到:
4 π v T c λ < π \frac{4 \pi v T_c}{\lambda}<\pi λ4πvTc<π
也就是说可以推出之前的结论,由此出发即可证明最大不模糊速度为:
v max = λ 4 T c v_{\max }=\frac{\lambda}{4 T_c} vmax=4Tcλ
3、最大不模糊角度
最大不模糊角度就是不产生栅瓣的FOV,即不产生角度混叠的FOV。我们可以认为雷达对空间的采样率是由阵元的间距d来决定的,即可以用下列公式表示:
f s = 1 d f_s=\frac{1}{d} fs=d1
其中,d越大即空间采样率越小,d越小对空间的采样率越大,我们会推导d为什么小于半波长不会出现栅瓣(混叠)。
这里我们同样会遇到一个问题,即 2 π d sin ( θ ) λ < π \frac{2 \pi d \sin (\theta)}{\lambda}<\pi λ2πdsin(θ)<π ,为什么要满足这个不等式,下图中虽然可以从几何角度理解,但我还是想从公式推导。
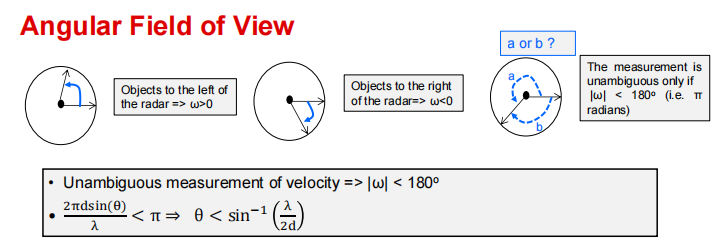
同理,我们先假定当前的空间采样率已经满足了某个最大的FOV,我们可以得到:
f s = 1 d ≥ 2 f f_s=\frac{1}{d} \geq 2 f fs=d1≥2f
其中,f是什么呢?本平台为同步更新,更多实时内容请移步:从奈奎斯特采样定理推导FMCW雷达系统性能参数 进行查看,希望大家都学有所获。
注:本文为调皮哥空闲时的心得和体会,由小助理整编,不涉及任何利益,内容有说错或不全面的地方,烦请大家批评指正!