题目链接:215. 数组中的第K个最大元素 - 力扣(LeetCode)
题干:
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
题目分析:
看到找第k大、前k大的数据我们能想到的解决方案就两种
- 排序,然后找到第k个位置的值
- 建堆
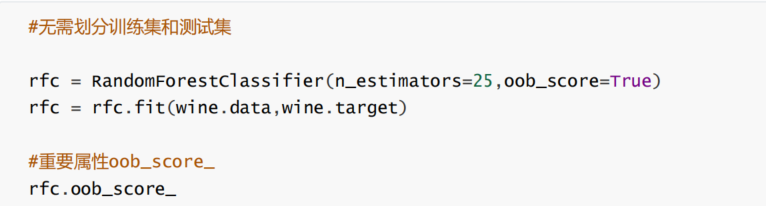
这里如果我们直接使用排序来做这道题未免有点太挫了,效率太低,所以我们首选建堆。默认建大堆,建堆之后pop的第k次的结果就是我们要找的值。
优化:这里对于整个数组建堆,如果数组很大,但是k较小,那么上面的解法的效率就不够极致,这时候,我们其实可以考虑建一个k个元素的小堆,然后遍历整个数组,判断当前堆顶的数据和nums[i]的大小,如果nums[i]更大的话,就pop堆顶的数据,然后插入nums[i]到堆中,然后插入数组中的数据,当遍历完整个数组的时候,前k大的数据就在我们建的堆里面了,此时第k大的数就是堆顶的元素。对于这种解法,其时间复杂度为O(K+(N-K)logK)。
代码实现:
//解法一
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int> heap(nums.begin(), nums.end());
while(--k)
{
heap.pop();
}
return heap.top();
}
};
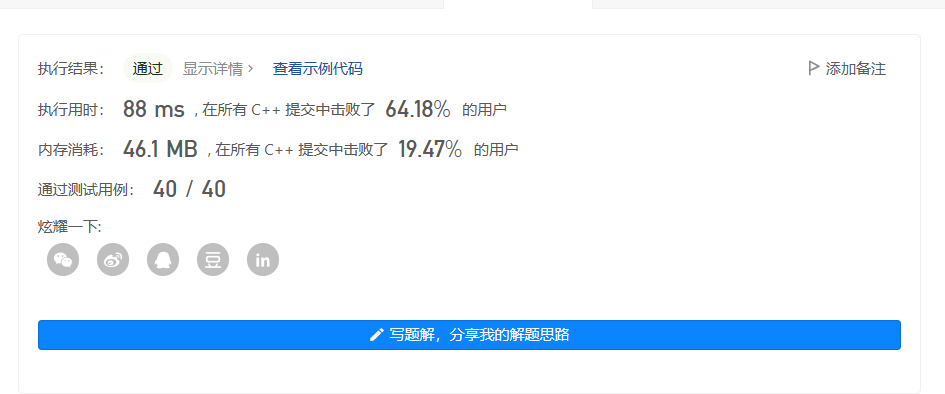
//优化
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int, vector<int>, greater<int>> heap(nums.begin(), nums.begin() + k);
for(size_t i = k; i < nums.size(); ++i)
{
if(nums[i] > heap.top())
{
heap.pop();
heap.push(nums[i]);
}
}
return heap.top();
}
};














![[Java 数据结构] 反射、枚举和lambda表达式](https://img-blog.csdnimg.cn/049b1f93e06f4114ad9d2d360c0b07a6.png)