文章目录
- 图的遍历
- 深度优先遍历
- 对于无向图的邻接矩阵的深度优先遍历
- 无向非连通图的深度优先遍历
- 对于无向图的邻接表的深度优先遍历
- 非递归实现深度优先遍历
- 无向图的邻接矩阵代码实现
- 无向图的邻接表代码实现
- 递归和非递归的同异
- 广度优先遍历
- 邻接表BFS
- 邻接矩阵BFS
- 图的应用
- 生成树
- 无向图的生成树
- 最小生成树
- prim算法
- Kruskal算法
- 最短路径
- Dijkstra算法
- Floyd-Warshall算法
- Dijkstra算法和Floyd算法的对比
- 拓扑排序
- AOV网的特点
- 拓扑排序的方法
- 代码实现
- 检测AOV网中是否存在环的方法
- 最短路径
- 用AOE网表示工程计划
- 求解关键路径
- 确定关键路径
- 求关键路径步骤
- 代码实现
图的遍历
图的遍历定义:从已给的连通图中某一顶点出发,沿着一些边遍历图中的所有顶点,且使每个顶点仅被访问一次。
**图的特点:**图中可能存在回路,且图的任一顶点都可能与其他顶点相通,在访问完某个顶点之后可能会沿着某些边又回到了曾经访问过的顶点。
怎么避免重复访问?
解决思路:设置==辅助数组==visited[n],用来标记每个被访问过的顶点。
- 初始状态
visited[i]为0 - 顶点 i 被访问,改
visited[i]为1,防止被多次访问。
图的遍历分两种:
- 深度优先搜索(DFS)(Depth_First Search)
- 广度优先搜索(BFS)(Breadth_Frist Search)
深度优先遍历
深度优先遍历的主要思想是沿着当前顶点的某一条路径尽可能深入,直到无法继续深入,然后回溯到前一个顶点,继续访问其他未被访问的相邻顶点。其实现过程可以分为以下几个步骤:
- **选择起始顶点:**选择一个起始顶点作为深度优先遍历的起点。
- **访问顶点并标记:**访问当前顶点,并将其标记已访问,以避免在之后的遍历过程中重复访问。
- **遍历相邻顶点:**检查当前顶点的所有相邻顶点。对于每个未被访问过的相邻顶点,递归地进行深度优先遍历。这样可以沿着一条路径尽可能的深入。
- **回溯:**当无法继续深入时,回溯到前一个顶点,继续访问其他未被访问过的相邻顶点。
- **遍历结束:**当所有与起始顶点连通的顶点都被访问到后,深度优先遍历结束。
深度优先遍历可以通过**递归和非递归(使用栈)**的方式实现。递归实现通常更简洁,但是可能会导致栈溢出。非递归实现则可以避免栈溢出的问题发生。
递归实现的核心思想是将当前顶点作为参数,递归调用DFS函数。在DFS函数中,首先访问并标记当前顶点,然后遍历所有相邻顶点,对于未被访问过的相邻顶点,再次调用DFS函数。
非递归实现则需要手动模拟函数调用栈的行为。首先将起始顶点入栈,然后进行循环,每次从栈顶取出一个顶点并访问,将其相邻的未被访问过的顶点入栈。循环终止的条件是栈为空,此时遍历完成。
需要注意的是,无论是递归还是非递归实现,都需要用一个数组或者其他数据结构记录已访问过的顶点,以避免重复访问。另外,深度优先遍历的时间复杂度与图的表示方式有关。对于邻接矩阵表示的图,时间复杂度为O(n^2);对于邻接表表示的图,时间复杂度为O(n+e),其中n表示顶点数,e表示边数。
下面我会依次介绍这几种表示方法和实现过程。
对于无向图的邻接矩阵的深度优先遍历
实现过程:
实现过程和思路大抵和上面的一样,简单回顾一下
- 初始化邻接矩阵和访问标记数组。
- 定义递归函数DFS,接受当前顶点索引作为参数。
- 访问当前顶点并标记为已访问。
- 遍历邻接顶点,递归调用DFS函数处理未访问过的邻接顶点。
- 回溯到前一个顶点,继续处理其他未访问过的邻接顶点。
- 遍历结束条件:所有与起始顶点连通的顶点都被访问过。如果图不是连通的,需要从其他未访问过的顶点开始新一轮遍历。
- 在主函数中调用DFS函数,传入起始顶点的索引。
代码实现:
假设我们有一个无向图,顶点有A, B, C, D, E,边有(A, B), (A, C), (B, D), (C, E), (D, E),用邻接矩阵表示如下:
A B C D E
A 0 1 1 0 0
B 1 0 0 1 0
C 1 0 0 0 1
D 0 1 0 0 1
E 0 0 1 1 0
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#define N 5 //图的顶点数
//邻接矩阵表示图
int graph[N][N]={
{0, 1, 1, 0, 0},
{1, 0, 0, 1, 0},
{1, 0, 0, 0, 1},
{0, 1, 0, 0, 1},
{0, 0, 1, 1, 0}
};
//访问标记数组
bool visited[N]={false};
/*
* 标记数组也可用0 和 1 代替
* int visited[N] = {0};
* 下面标记顶点已访问用
* visited[v] = 1;
*/
//深度优先遍历
void DFS (int v)
{
//输出当前顶点
printf("%c",'A'+v);
//标记当前顶点已访问
visited[v]=true;
//遍历顶点v的邻接顶点
for(int i=0;i<N;i++)
{
//判断顶点i是否与顶点v相邻且未访问过
if(graph[v][i]==1&&!visited[i])
{
DFS(i); // 递归调用DFS函数,处理邻接顶点i
}
}
}
int main() {
printf("DFS遍历结果:\n");
// 从顶点0开始遍历(即顶点A)
DFS(0);
printf("\n");
return 0;
}
无向非连通图的深度优先遍历
对于无向非连通图,我们需要对所有的顶点执行深度优先遍历,以确保访问到所有的连通分量。我们可以在主函数中使用循环来遍历所有顶点,然后对未访问过的顶点执行深度优先遍历。
假设我们有以下无向非连通图:
A---B E
\ / |
C F
|
D
int graph[N][N] = {
{0, 1, 1, 0, 0, 0},
{1, 0, 0, 1, 0, 0},
{1, 0, 0, 0, 0, 0},
{0, 1, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 1},
{0, 0, 0, 0, 1, 0}
};
代码实现:
#include <stdio.h>
#include <stdbool.h>
#define N 6 // 图的顶点数量
int graph[N][N] = {
{0, 1, 1, 0, 0, 0},
{1, 0, 0, 1, 0, 0},
{1, 0, 0, 0, 0, 0},
{0, 1, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 1},
{0, 0, 0, 0, 1, 0}
};
// 访问标记数组
bool visited[N] = {false};
// 深度优先遍历
void DFS(int v) {
// 输出当前顶点
printf("%c ", 'A' + v);
// 标记当前顶点为已访问
visited[v] = true;
// 遍历顶点v的邻接顶点
for (int i = 0; i < N; i++) {
// 判断顶点i是否与顶点v相邻且未访问过
if (graph[v][i] == 1 && !visited[i]) {
DFS(i); // 递归调用DFS函数,处理邻接顶点i
}
}
}
int main() {
printf("DFS遍历结果:\n");
// 遍历所有顶点
for (int i = 0; i < N; i++) {
// 如果顶点i未访问过,则从顶点i开始进行深度优先遍历
if (!visited[i]) {
DFS(i);
printf("\n"); // 换行,以区分连通分量
}
}
return 0;
}
对于无向图的邻接表的深度优先遍历
-
定义邻接表的数据结构:为了表示图,我们使用顶点数组和边数组。顶点数组存储顶点信息,边数组存储邻接顶点的信息。在我们的例子中,我们定义了
VertexNode和EdgeNode结构体分别表示顶点和边。 -
创建图:我们需要根据给定的顶点和边信息创建邻接表。
createGraph()函数完成了这个任务。它首先将顶点信息添加到顶点数组中,然后根据给定的边信息,将边信息添加到邻接表中。对于无向图,我们需要添加两条边(从顶点a到顶点b,从顶点b到顶点a)。-
说明创建图的过程的代码,因为代码比较冗余。
-
具体来说,对于一条边从顶点a到顶点b,它会创建一个新的边结构体newNodeA,并将其adjvex成员设置为顶点b的索引,同时将其next指针指向顶点a当前的第一个邻接顶点。然后,它将顶点a的firstEdge指针更新为新创建的边结构体newNodeA,这样,newNodeA成为了顶点a的第一个邻接顶点。
接下来,它会创建另一个新的边结构体newNodeB,并将其adjvex成员设置为顶点a的索引,同时将其next指针指向顶点b当前的第一个邻接顶点。然后,它将顶点b的firstEdge指针更新为新创建的边结构体newNodeB,这样,newNodeB成为了顶点b的第一个邻接顶点。由于这是一个无向图,所以我们需要在这两个顶点之间建立双向连接。
-
-
初始化访问标记数组:我们使用一个布尔数组
visited来记录每个顶点是否已经访问过。初始时,所有顶点都未访问,所以数组中的所有元素都设为false。 -
深度优先遍历(递归):从一个顶点(例如,顶点A)开始,我们首先访问并输出它,然后将其标记为已访问。接下来,我们遍历该顶点的所有邻接顶点。对于每个未访问的邻接顶点,我们递归地调用DFS函数。这样,我们将不断沿着图的边向更深的顶点移动,直到到达一个没有未访问邻接顶点的顶点。此时,递归开始回溯,返回到前一个顶点,继续遍历其他邻接顶点。整个过程将持续到所有与初始顶点连通的顶点都被访问。
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define N 5 // 图的顶点数量
// 边的结构体定义
typedef struct EdgeNode {
int adjvex; // 邻接顶点
struct EdgeNode* next; // 指向下一个邻接顶点的指针
} EdgeNode;
// 顶点的结构体定义
typedef struct VertexNode {
char data; // 顶点数据(这里用字母表示)
EdgeNode* firstEdge; // 指向第一个邻接顶点的指针
} VertexNode;
// 邻接表定义
VertexNode adjList[N];
// 访问标记数组
bool visited[N] = {false};
// 创建图的邻接表表示的函数
void createGraph() {
// 添加顶点信息
for (int i = 0; i < N; i++) {
adjList[i].data = 'A' + i; // 设置顶点的数据(字母)
adjList[i].firstEdge = NULL; // 初始化邻接顶点指针为空
}
// 添加边信息(无向图)
int edges[][2] = {{0, 1}, {0, 2}, {1, 3}, {2, 4}, {3, 4}}; // 定义边关系数组
int numEdges = sizeof(edges) / sizeof(edges[0]); // 计算边的数量
// 遍历所有边
for (int i = 0; i < numEdges; i++) {
int a = edges[i][0]; // 获取第i条边的第一个顶点
int b = edges[i][1]; // 获取第i条边的第二个顶点
// 创建一个新的边结构体(newNodeA),用于表示从顶点a到顶点b的连接
EdgeNode* newNodeA = (EdgeNode*) malloc(sizeof(EdgeNode));
newNodeA->adjvex = b; // 设置邻接顶点为顶点b
newNodeA->next = adjList[a].firstEdge; // 将新节点的next指针指向顶点a当前的第一个邻接顶点
adjList[a].firstEdge = newNodeA; // 更新顶点a的firstEdge指针,使其指向新节点
// 创建一个新的边结构体(newNodeB),用于表示从顶点b到顶点a的连接(因为是无向图,所以需要添加双向连接)
EdgeNode* newNodeB = (EdgeNode*) malloc(sizeof(EdgeNode));
newNodeB->adjvex = a; // 设置邻接顶点为顶点a
newNodeB->next = adjList[b].firstEdge; // 将新节点的next指针指向顶点b当前的第一个邻接顶点
adjList[b].firstEdge = newNodeB; // 更新顶点b的firstEdge指针,使其指向新节点
}
}
void DFS(int v) {
// 输出当前顶点
printf("%c ", adjList[v].data);
// 标记当前顶点为已访问
visited[v] = true;
// 遍历顶点v的邻接顶点
for (EdgeNode* p = adjList[v].firstEdge; p != NULL; p = p->next) {
int w = p->adjvex; // 获取邻接顶点的索引
// 判断顶点w是否未访问过
if (!visited[w]) {
DFS(w); // 递归调用DFS函数,处理邻接顶点w
}
}
}
int main() {
// 创建图的邻接表表示
createGraph();
printf("DFS遍历结果:\n");
// 从顶点0开始遍历(即顶点A)
DFS(0);
printf("\n");
return 0;
}
非递归实现深度优先遍历
无向图的邻接矩阵代码实现
思路:
-
定义图和栈的数据结构,图使用邻接矩阵表示,栈用于存储待访问的顶点。
-
初始化图,设置顶点数量和邻接矩阵的元素值。
-
添加边到图中,根据给定的顶点对,在邻接矩阵中更新对应的边。
-
实现非递归DFS遍历函数:
- 定义一个访问标记数组,用于记录每个顶点是否被访问过。
- 初始化栈,并将起始顶点入栈。
- 用一个循环结构遍历栈,当栈不为空时,执行下面的操作
- 弹出栈顶顶点。
- 输出当前访问的顶点。
- 遍历邻接矩阵,找到当前顶点的所有未访问邻居。
- 将未访问邻居入栈,并标记为已访问。
注意点:
-
当图中存在自环或重边时,需要对添加边的操作进行额外处理。
-
如果图中有多个连通分量,需要对每个连通分量进行DFS遍历。
-
在实际应用中,可能需要处理更大规模的图。在这种情况下,应考虑使用动态内存分配,而非使用固定大小的数组。
时间复杂度:由于需要遍历所有顶点和边,因此时间复杂度为O(V+E),其中V是顶点数,E是边数。
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX_VERTEX 100
// 邻接矩阵表示的图
typedef struct Graph {
int vertex_num; // 顶点数量
int matrix[MAX_VERTEX][MAX_VERTEX]; // 邻接矩阵
} Graph;
// 栈结构
typedef struct Stack {
int data[MAX_VERTEX];
int top;
} Stack;
// 初始化栈
void init_stack(Stack *stack) {
stack->top = -1; // 将栈顶指针初始化为-1,表示空栈
}
// 判断栈是否为空
bool is_empty(Stack *stack) {
return stack->top == -1; // 当栈顶指针为-1时,表示栈为空
}
// 入栈
void push(Stack *stack, int value) {
stack->data[++stack->top] = value; // 将栈顶指针加1,然后将元素放入栈顶位置
}
// 出栈
int pop(Stack *stack) {
return stack->data[stack->top--]; // 返回栈顶元素,并将栈顶指针减1
}
// 深度优先搜索(DFS)非递归实现
void DFS_non_recursive(Graph *graph, int start_vertex) {
bool visited[MAX_VERTEX] = {false}; // 初始化访问标记数组,初始状态下所有顶点均未访问
Stack stack; // 声明一个栈用于存储待访问的顶点
init_stack(&stack); // 初始化栈
push(&stack, start_vertex); // 将起始顶点入栈
visited[start_vertex] = true; // 标记起始顶点为已访问
// 当栈不为空时,继续进行DFS遍历
while (!is_empty(&stack)) {
int current_vertex = pop(&stack); // 弹出栈顶元素
printf("访问顶点:%d\n", current_vertex); // 输出当前访问的顶点
// 遍历邻接矩阵,找到当前顶点的所有未访问邻居
for (int i = 0; i < graph->vertex_num; ++i) {
if (graph->matrix[current_vertex][i] != 0 && !visited[i]) {
push(&stack, i); // 将未访问邻居入栈
visited[i] = true; // 标记为已访问
}
}
}
}
// 初始化图
void init_graph(Graph *graph, int vertex_num) {
graph->vertex_num = vertex_num; // 设置顶点数量
// 初始化邻接矩阵,所有元素都为0
for (int i = 0; i < vertex_num; ++i) {
for (int j = 0; j < vertex_num; ++j) {
graph->matrix[i][j] = 0;
}
}
}
// 添加边
void add_edge(Graph *graph, int u, int v) {
graph->matrix[u][v] = 1; // 在邻接矩阵中将顶点u和v之间的边设为1
graph->matrix[v][u] = 1; // 由于是无向图,需要将v和u之间的边也设为1
}
// 主函数
int main() {
int vertex_num = 5; // 设置顶点数量
Graph graph; // 声明一个图结构体变量
init_graph(&graph, vertex_num); // 初始化图
// 添加边
add_edge(&graph, 0, 1);
add_edge(&graph, 1, 2);
add_edge(&graph, 2, 3);
add_edge(&graph, 3, 4);
add_edge(&graph, 4, 0);
printf("DFS非递归遍历结果:\n");
DFS_non_recursive(&graph, 0); // 从顶点0开始进行DFS非递归遍历
return 0;
}
说明一下 DFS_non_recursive的代码实现过程:
-
定义一个布尔数组
visited,用于记录每个顶点是否被访问过。初始时,所有顶点的访问状态都是false。 -
定义一个栈
stack,用于存储待访问的顶点。首先调用init_stack函数初始化栈。 -
将起始顶点
start_vertex压入栈中,并将其对应的访问状态设为true。 -
使用一个
while循环,当栈非空时执行以下操作:a. 弹出栈顶元素,将其赋值给
current_vertex。输出当前访问的顶点。b. 遍历邻接矩阵,寻找当前顶点
current_vertex的所有未访问过的邻居。c. 对于每个未访问的邻居,将其压入栈中,并将其访问状态设为
true。
这个过程会一直执行,直到栈为空。在整个过程中,算法会沿着一条路径尽可能深入地访问顶点,直到无法继续前进为止,然后回溯并继续探索其他分支。
无向图的邻接表代码实现
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX_VERTICES 100
// 定义邻接表节点结构体
typedef struct node {
int vertex;
struct node* next;
} Node;
// 定义图结构体
typedef struct graph {
int num_vertices;
Node* adj_list[MAX_VERTICES];
} Graph;
// 创建新节点的函数
Node* create_node(int v) {
// 分配内存并初始化新节点
Node* new_node = (Node*)malloc(sizeof(Node));
new_node->vertex = v;
new_node->next = NULL;
return new_node;
}
// 初始化图的函数
Graph* create_graph(int vertices) {
// 分配内存并初始化图结构体
Graph* g = (Graph*)malloc(sizeof(Graph));
g->num_vertices = vertices;
// 初始化邻接表,将所有顶点的邻接表指针设置为NULL
for (int i = 0; i < vertices; i++) {
g->adj_list[i] = NULL;
}
return g;
}
// 添加边的函数
void add_edge(Graph* g, int src, int dest) {
// 在源顶点的邻接表中添加目标顶点
// 首先创建一个新节点,用于表示目标顶点
Node* new_node = create_node(dest);
// 将新节点添加到源顶点的邻接表中
new_node->next = g->adj_list[src];
g->adj_list[src] = new_node;
// 无向图需要在目标顶点的邻接表中也添加源顶点
// 首先创建一个新节点,用于表示源顶点
new_node = create_node(src);
// 将新节点添加到目标顶点的邻接表中
new_node->next = g->adj_list[dest];
g->adj_list[dest] = new_node;
}
// DFS的递归实现
void dfs(Graph* g, int vertex, bool visited[]) {
// 标记当前顶点为已访问,并输出顶点编号
visited[vertex] = true;
printf("Visited %d\n", vertex);
// 遍历与当前顶点相邻的所有顶点
Node* temp = g->adj_list[vertex];
while (temp) {
int adj_vertex = temp->vertex;
// 如果相邻顶点尚未访问,递归进行DFS
if (!visited[adj_vertex]) {
dfs(g, adj_vertex, visited);
}
// 继续检查下一个相邻顶点
temp = temp->next;
}
}
// DFS遍历函数
void depth_first_search(Graph* g, int start_vertex) {
// 为访问状态数组分配内存并初始化为false
bool visited[g->num_vertices];
for (int i = 0; i < g->num_vertices; i++) {
visited[i] = false;
}
// 从起始顶点开始DFS遍历
dfs(g, start_vertex, visited);
}
int main() {
// 创建一个包含4个顶点的图
Graph* g = create_graph(4);
// 添加边
add_edge(g, 0, 1);
add_edge(g, 0, 2);
add_edge(g, 1, 2);
add_edge(g, 1, 3);
// 从顶点0开始进行深度优先遍历
depth_first_search(g, 0);
// 释放图结构体的内存
for (int i = 0; i < g->num_vertices; i++) {
Node* temp = g->adj_list[i];
while (temp) {
Node* next_node = temp->next;
free(temp);
temp = next_node;
}
}
free(g);
return 0;
}
递归和非递归的同异
相同:
无论是递归还是非递归实现,DFS的基本原理都是沿着一条路径尽可能深入地访问顶点,直到无法继续前进为止,然后回溯并继续探索其他分支。
不同:
- 递归实现:通过函数自身的调用来模拟遍历过程。当一个顶点被访问时,递归调用DFS函数,将该顶点的所有未访问邻居作为参数传入。
- 非递归实现:通过使用栈数据结构和循环来模拟遍历过程。将待访问的顶点入栈,然后通过循环不断弹出栈顶顶点,并将其未访问邻居入栈。
系统资源消耗:
- 递归实现:每次递归调用都会占用系统栈空间。当图的规模较大或深度较深时,可能导致栈溢出错误。
- 非递归实现:使用自定义的栈来管理待访问顶点,不依赖系统栈。因此,非递归实现在空间和时间效率上通常更优。
广度优先遍历
对于广度优先遍历算法,它是一种按层级遍历图的方法。从一个起始顶点开始,首先访问所有与其相邻的顶点,然后再按照相同的方法访问这些相邻顶点的邻居。通常使用队列来实现BFS。

类似于二叉树的层序遍历。
邻接表BFS
实现步骤:
- 初始化访问标记数组和队列。访问标记数组用于标记结点是否已经被访问过,队列用于存储待访问的结点。
- 将起始结点加入队列,并将其标记为已访问。
- 取出队列的头结点,遍历它的所有邻居结点。如果邻居结点未被访问过,则将其加入队列,并将其标记为已访问。
- 重复步骤3,直到队列为空。
下面是BFS遍历在邻接表中的具体实现过程,假设要从结点0开始进行BFS遍历:
- 初始化访问标记数组和队列
int visited[MAX_VERTEX_NUM] = {0};
Queue Q;
InitQueue(&Q);
- 将起始结点加入队列,并将其标记为已访问。
EnQueue(&Q, 0);
visited[0] = 1;
- 取出队列的头结点0,遍历它的所有邻居结点1和2,如果邻居节点未被访问过,则将其加入队列,并将其标记为已访问。
while (!IsEmpty(&Q)) {
int data = DeQueue(&Q);
printf("%d ", data); // 访问节点
ArcNode *p = G->vertex[data].firstArc;
while (p != NULL) {
int adjvex = p->adjvex;
if (visited[adjvex] == 0) {
EnQueue(&Q, adjvex);
visited[adjvex] = 1;
}
p = p->next;
}
}
- 重复步骤3,直到队列为空。
具体的举例实现:
假设有以下图的邻接表表示:
0 -> 1 -> 2 -> 3
1 -> 0 -> 4
2 -> 0 -> 4 -> 5
3 -> 0 -> 5
4 -> 1 -> 2 -> 5
5 -> 2 -> 3 -> 4
我们从节点0开始进行BFS遍历。按照上述步骤,具体的执行过程如下:
- 创建一个队列,并将起点节点0放入队列中。
队列:0
- 创建一个标记数组,将节点0标记为已访问。
标记数组:[1, 0, 0, 0, 0, 0]
- 从队列中取出节点0,并访问该节点。将它的邻居节点1、2、3加入队列中,并将它们标记为已访问。
队列:1, 2, 3
标记数组:[1, 1, 1, 1, 0, 0]
- 从队列中取出节点1,并访问该节点。将它的邻居节点0、4加入队列中,并将它们标记为已访问。
队列:2, 3, 0, 4
标记数组:[1, 1, 1, 1, 1, 0]
- 从队列中取出节点2,并访问该节点。将它的邻居节点0、4、5加入队列中,并将它们标记为已访问。
队列:3, 0, 4, 5
标记数组:[1, 1, 1, 1, 1, 1]
- 从队列中取出节点3,并访问该节点。将它的邻居节点0、5加入队列中,并将它们标记为已访问。
队列:0, 4, 5
标记数组:[1, 1, 1, 1, 1, 1]
- 从队列中取出节点0,并访问该节点。它的所有邻居节点已经被访问过,不需要再加入队列。
队列:4, 5
标记数组:[1, 1, 1, 1, 1, 1]
- 从队列中取出节点4,并访问该节点。将它的邻居节点1、2、5加入队列中,并将它们标记为已访问。
队列:5, 1, 2
标记数组:[1, 1, 1, 1, 1, 1]
- 从队列中取出节点5,并访问该节点。将它的邻居节点2、3、4加入队列中,并将它们标记为已访问。
队列:1, 2, 3, 4
标记数组:[1, 1, 1, 1, 1, 1]
- 从队列中取出节点1,并访问该节点。它的所有邻居节点已经被访问过,不需要再加入队列。
队列:2, 3, 4
标记数组:[1, 1, 1, 1, 1, 1]
- 从队列中取出节点2,并访问该节点。它的所有邻居节点已经被访问过,不需要再加入队列。
队列:3, 4
标记数组:[1, 1, 1, 1, 1, 1]
- 从队列中取出节点3,并访问该节点。它的所有邻居节点已经被访问过,不需要再加入队列。
队列:4
标记数组:[1, 1, 1, 1, 1, 1]
- 从队列中取出节点4,并访问该节点。它的所有邻居节点已经被访问过,不需要再加入队列。
队列:空
标记数组:[1, 1, 1, 1, 1, 1]
- 遍历结束。
通过以上步骤,我们可以得到节点0、1、2、3、4、5的BFS遍历结果为:0、1、2、3、4、5。
代码实现
#include <stdio.h>
#include <stdlib.h>
#define MAX_NODES 6 // 图中节点数
// 邻接表结构体定义
struct Node {
int val; // 节点值
struct Node* next; // 指向下一个节点的指针
};
// 创建邻接表节点
struct Node* createNode(int val) {
struct Node* newNode = (struct Node*) malloc(sizeof(struct Node)); // 分配新节点内存
newNode->val = val; // 设置节点值
newNode->next = NULL; // 设置下一个节点指针为空
return newNode;
}
// 添加边
void addEdge(struct Node* adjList[], int src, int dest) {
// 将dest节点添加到src节点的邻接表中
struct Node* newNode = createNode(dest);
newNode->next = adjList[src];
adjList[src] = newNode;
}
// BFS遍历邻接表
void bfs(struct Node* adjList[], int startNode) {
int visited[MAX_NODES] = {0}; // 创建标记数组并初始化为0
struct Node* queue[MAX_NODES]; // 创建队列
int front = 0, rear = 0; // 初始化队列指针
queue[rear++] = adjList[startNode]; // 将起点节点入队
visited[startNode] = 1; // 标记起点节点为已访问
while (front < rear) { // 当队列不为空时,执行以下操作
struct Node* currNode = queue[front++]; // 取出队列头节点
printf("%d ", currNode->val); // 访问节点
struct Node* adjNode = currNode->next; // 取出当前节点的第一个邻居节点
while (adjNode) { // 遍历当前节点的所有邻居节点
if (!visited[adjNode->val]) { // 如果邻居节点未被访问过
visited[adjNode->val] = 1; // 标记邻居节点为已访问
queue[rear++] = adjList[adjNode->val]; // 将邻居节点入队
}
adjNode = adjNode->next; // 移动到下一个邻居节点
}
}
}
// 主函数
int main() {
struct Node* adjList[MAX_NODES] = {0}; // 创建邻接表并初始化为空
// 添加边
addEdge(adjList, 0, 1);
addEdge(adjList, 0, 2);
addEdge(adjList, 0, 3);
addEdge(adjList, 1, 0);
addEdge(adjList, 1, 4);
addEdge(adjList, 2, 0);
addEdge(adjList, 2, 4);
addEdge(adjList, 2, 5);
addEdge(adjList, 3, 0);
addEdge(adjList, 3, 5);
addEdge(adjList, 4, 1);
addEdge(adjList, 4, 2);
addEdge(adjList, 4, 5);
addEdge(adjList, 5, 2);
addEdge(adjList, 5, 3);
addEdge(adjList, 5, 4);
printf("BFS遍历结果:");
bfs(adjList, 0); // 从节点0开始进行BFS遍历
return 0;
}
在邻接表中,BFS遍历的时间复杂度为O(V+E),其中V表示图中节点数,E表示边数。这是因为BFS遍历会访问所有的节点和边,每个节点最多被访问一次,每条边最多被访问两次(一次在它所属的节点被访问时,另一次在它所连接的节点被访问时),因此总的时间复杂度为O(V+E)。
邻接矩阵BFS
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX_NODES 6 // 图中节点数
// BFS遍历邻接矩阵
void bfs(int adjMatrix[][MAX_NODES], int startNode) {
bool visited[MAX_NODES] = {false}; // 创建标记数组并初始化为false
int queue[MAX_NODES]; // 创建队列
int front = 0, rear = 0; // 初始化队列指针
queue[rear++] = startNode; // 将起点节点入队
visited[startNode] = true; // 标记起点节点为已访问
while (front < rear) { // 当队列不为空时,执行以下操作
int currNode = queue[front++]; // 取出队列头节点
printf("%d ", currNode); // 访问节点
for (int i = 0; i < MAX_NODES; i++) { // 遍历所有节点
if (adjMatrix[currNode][i] == 1 && !visited[i]) { // 如果节点i与当前节点相邻且未被访问过
visited[i] = true; // 标记节点i为已访问
queue[rear++] = i; // 将节点i入队
}
}
}
}
// 主函数
int main() {
int adjMatrix[MAX_NODES][MAX_NODES] = {0}; // 创建邻接矩阵并初始化为0
// 添加边
adjMatrix[0][1] = 1;
adjMatrix[0][2] = 1;
adjMatrix[0][3] = 1;
adjMatrix[1][0] = 1;
adjMatrix[1][4] = 1;
adjMatrix[2][0] = 1;
adjMatrix[2][4] = 1;
adjMatrix[2][5] = 1;
adjMatrix[3][0] = 1;
adjMatrix[3][5] = 1;
adjMatrix[4][1] = 1;
adjMatrix[4][2] = 1;
adjMatrix[4][5] = 1;
adjMatrix[5][2] = 1;
adjMatrix[5][3] = 1;
adjMatrix[5][4] = 1;
printf("BFS遍历结果:");
bfs(adjMatrix, 0); // 从节点0开始进行BFS遍历
return 0;
}
图的应用
生成树
**生成树的概念:**它是一种将图中所有无环连通子图,同时具有最小权重和。
- 图中所有顶点均有边连接起来,但是不存在回路的图。
- 包括无向图G所有顶点的极小连通子图。
如:图 234 就是由包含图 1 所有顶点的极小连通子图。
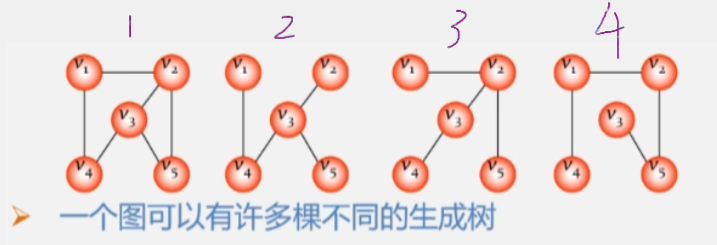
最小生成树的求解主要有两种经典算法:Kruskal算法和Prim算法。它们的核心思想是贪心算法,即在每一步都选择当前最优解,最终得到全局最优解。
生成树的特点:
-
**连通性:**生成树保留了原图的连通性,确保任意两个顶点之间存在至少一条路径。这意味着,从任何一个顶点出发,都可以到达其他顶点。
-
**无环:**生成树中不存在环,因为环会导致多余的边。生成树中去掉任意一条边后,图将变得不连通。
-
**边数:**在一个有n个顶点的连通无向图中,生成树的边数恒定为n-1。这是因为在树中,边数总是等于顶点数减1。
-
**数量:**一个连通无向图可能有多个生成树,这取决于选择哪些边构成子图。生成树的数量可能会因图的结构、顶点和边的数量而有所不同。
-
**子图:**生成树是原图的一个子图,它包含了原图中所有的顶点和部分边。这意味着生成树可以用原图中的部分边组成,而不需要引入新的顶点或边。
-
最小生成树
无向图的生成树
实现无向图生成树的过程可以通过深度优先遍历和广度优先遍历来实现。
以深度优先遍历为例:
即深度优先遍历图中所有的顶点,然后在访问的过程中,把走过的这些边加到生成树上,就可以得到生成树了。
#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
#include <string.h>
// 图的顶点数量
#define V 5
// 定义图的数据结构
typedef struct Graph {
int vertices; // 顶点数量
int** adj_matrix; // 邻接矩阵表示的图
} Graph;
// 初始化图
void init_graph(Graph* g, int vertices) {
g->vertices = vertices;
g->adj_matrix = (int**)malloc(vertices * sizeof(int*));
for (int i = 0; i < vertices; ++i) {
g->adj_matrix[i] = (int*)calloc(vertices, sizeof(int));
}
}
// 释放图占用的内存
void free_graph(Graph* g) {
for (int i = 0; i < g->vertices; ++i) {
free(g->adj_matrix[i]);
}
free(g->adj_matrix);
}
// 添加无向边
void add_edge(Graph* g, int u, int v) {
g->adj_matrix[u][v] = 1; // 将邻接矩阵对应位置设为1表示边存在
g->adj_matrix[v][u] = 1;
}
// 深度优先搜索
void dfs(Graph* g, int v, bool* visited, Graph* tree) {
visited[v] = true; // 标记顶点v已访问
for (int i = 0; i < g->vertices; ++i) {
// 如果顶点v和顶点i之间有边且顶点i未访问,则将边添加到生成树中,并递归进行深度优先搜索
if (g->adj_matrix[v][i] && !visited[i]) {
add_edge(tree, v, i);
dfs(g, i, visited, tree);
}
}
}
// 计算生成树
Graph spanning_tree(Graph* g) {
Graph tree;
init_graph(&tree, g->vertices);
bool visited[V];
memset(visited, false, sizeof(visited));
// 从顶点0开始深度优先搜索,构建生成树
dfs(g, 0, visited, &tree);
return tree;
}
// 打印图的邻接矩阵
void print_graph(Graph* g) {
for (int i = 0; i < g->vertices; ++i) {
for (int j = 0; j < g->vertices; ++j) {
printf("%d ", g->adj_matrix[i][j]);
}
printf("\n");
}
}
int main() {
Graph g;
init_graph(&g, V);
// 添加边,构建示例图
add_edge(&g, 0, 1);
add_edge(&g, 0, 2);
add_edge(&g, 1, 2);
add_edge(&g, 2, 3);
add_edge(&g, 3, 4);
printf("原始图的邻接矩阵:\n");
print_graph(&g);
Graph tree = spanning_tree(&g);
printf("\n生成树的邻接矩阵:\n");
print_graph(&tree);
free_graph(&g);
free_graph(&tree);
return 0;
}
最小生成树
- 通过一个带权值的无向网,可以构造多棵不同的生成树。
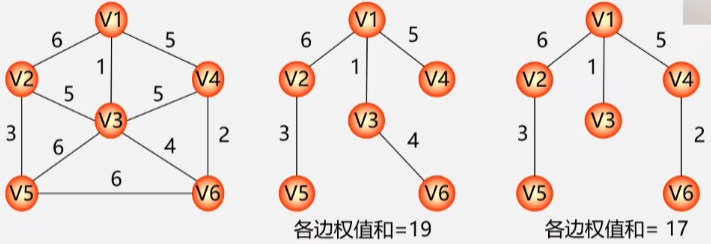
概念:
给定一个无向网络,在该网的所有生成树中,使得各边权值之和最小的那棵生成树称为该网的最小生成树,也叫最小代价生成树。
切割定理(Cut Property)
切割定理是最小生成树的一个重要性质,它为Prim算法和Kruskal算法的正确性提供了理论依据。
解释:
假设我们有一个连通网,我们将其顶点分成两个互不相交的子集U和V-U。现在我们观察这两个子集之间的边,这些边被称为横切边。我们选择一条权重最小的横切边,记为(u, v),其中u属于子集U,v属于子集V-U。
这个性质(切割定理)告诉我们,总是存在一个包含这条权重最小的横切边(u, v)的最小生成树。
换句话说,我们可以通过选择子集间权重最小的横切边,并将其加入到最小生成树中,逐步构建最小生成树。
举例说明:
假设我们有一个连通网,包含4个顶点A, B, C, D,以及4条边:
- A-B,权重为1
- A-C,权重为3
- B-D,权重为2
- C-D,权重为4
现在我们需要找到这个连通网的最小生成树。我们可以根据切割定理的性质来操作。
首先,我们将顶点集分为两个子集。让我们选取子集U包含顶点A,那么子集V-U将包含顶点B、C、D。接下来,我们观察连接这两个子集的横切边,有两条边满足条件:A-B和A-C。
在这两条横切边中,边A-B具有最小权重,为1。因此,我们可以将边A-B加入到最小生成树中。此时,子集U包含顶点A和B,子集V-U包含顶点C和D。
现在我们再次观察连接子集U和V-U的横切边,有两条边满足条件:B-D和A-C。在这两条横切边中,边B-D具有最小权重,为2。因此,我们将边B-D加入到最小生成树中。此时,子集U包含顶点A、B和D,子集V-U仅包含顶点C。
最后,我们观察连接子集U和V-U的横切边,只有一条边满足条件:A-C。我们将这条边加入到最小生成树中。
至此,我们已经找到了包含所有顶点的最小生成树,边为:A-B,B-D,A-C,总权重为1+2+3=6。
这个例子展示了如何根据切割定理逐步构建最小生成树。通过每次选择最小权重的横切边并将其加入生成树,我们最终得到了整个连通网的最小生成树。
prim算法
基本思想是从一个顶点开始,每次选取距离当前生成树最近的顶点并将其加入生成树,直到所有顶点都被加入生成树。
实现过程:
- 假设 N = (V,E) 是连通网,TE是 N 上最小生成树中边的集合。
- TE:在有 n 个顶点中的图中找到 n-1 条边,TE 里存着的就是这 n-1 条边,也就是最小生成树中所有的边。
- 初始令 U = {U0} (从某一个顶点开始构成最小生成树)(U0 ∈ V),令边集TE合为空 TE = { }。
- 这个 U0 就取 V1 来开始构成最小生成树。
- 采用 MST性质:那么 V1 就是 U 集合当中的一个顶点,其余顶点为 V-U 集合中的顶点。
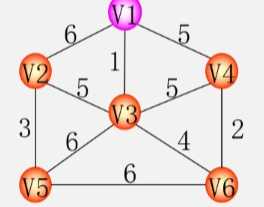
-
在所有 u∈U,v∈V-U 的边 (u,v)∈E 中,找一条权值最小的边 (U0,V0)。
-
将(U0,V0) 这条边并入边集合 TE,同时将这一条边相关联的顶点 V0 并入 U(放到最小生成树中)。
-
此时最小生成树上的顶点就有两个了。
-
剩下的 4 个顶点就是 V-U 集合中的顶点了。
-
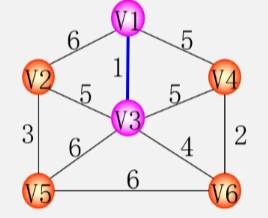
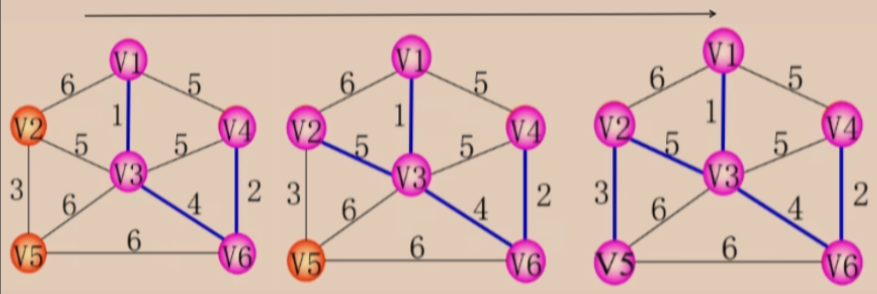
- 接下来继续找已经在生成树上的点,和不在生成树上的点之间,找一条权值最小的边,显然就是 V3 - V6 之间的权值最小。
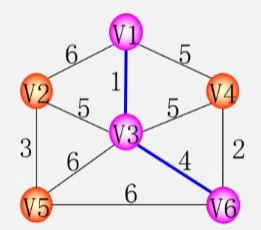
- 之后就是以此类推,从在树上的所有点和不在树上的所有点之间找一条权值最小的边。
- 将这条边以及这条边连接的点放入树中(边放入 TE ,点放入 U 中)。
- 重复上述操作直至 U=V(U集合包含所有的顶点) 为止,则 T = (V,TE) 为 N 的最小生成树。

代码实现
#include <stdio.h>
#include <stdbool.h>
#include <limits.h>
#define V 4
// 寻找并返回具有最小键值的尚未访问的顶点的索引
int minKey(int key[], bool mstSet[]) {
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++) {
if (mstSet[v] == false && key[v] < min) {
min = key[v];
min_index = v;
}
}
return min_index;
}
// 根据给定的父顶点数组和图,打印生成树的边和权重
void printMST(int parent[], int graph[V][V]) {
printf("Edge \tWeight\n");
for (int i = 1; i < V; i++)
printf("%d - %d \t%d \n", parent[i], i, graph[i][parent[i]]);
}
// 从给定图中构建并打印最小生成树
void primMST(int graph[V][V]) {
int parent[V]; // 用于存储生成树中的父顶点
int key[V]; // 用于存储图中顶点的键值
bool mstSet[V]; // 用于标记图中的顶点是否已被访问
// 初始化键值和访问标记
for (int i = 0; i < V; i++) {
key[i] = INT_MAX;
mstSet[i] = false;
}
key[0] = 0; // 将起始顶点的键值设为0,以便它被首先选中
parent[0] = -1; // 第一个顶点将是我们生成树的根节点,因此没有父顶点
// 遍历所有顶点
for (int count = 0; count < V - 1; count++) {
int u = minKey(key, mstSet); // 选择具有最小键值的尚未访问的顶点
mstSet[u] = true; // 将所选顶点标记为已访问
// 更新生成树中顶点的键值
for (int v = 0; v < V; v++) {
// 如果 u 和 v 之间有一条边,并且顶点 v 尚未访问,以及 u 和 v 之间的权重小于 v 的当前键值
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v]) {
parent[v] = u; // 更新父顶点
key[v] = graph[u][v]; // 更新键值
}
}
}
// 打印生成树的边和权重
printMST(parent, graph);
}
int main() {
int graph[V][V] = {
{0, 2, 0, 6},
{2, 0, 3, 8},
{0, 3, 0, 9},
{6, 8, 9, 0}
};
primMST(graph);
return 0;
}
Kruskal算法
它的基本思想是:将图中的边按照权重从小到大排序,然后从最小权重的边开始逐步添加到生成树中,直到最后生成树包含所有顶点。在添加边的过程中,需要确保新加入的边不会形成环。
Kruskal算法的实现过程:
- 将图中所有的边按权重从小到大排序。
- 初始化一个空的最小生成树结果集。
- 使用并查集来跟踪每个顶点所在的子集,以避免形成环。初始时,每个顶点都是一个独立的子集。
- 遍历排序后的边,对于每一条边: a. 使用并查集找到两个端点所在的子集。 b. 如果两个端点在不同的子集中,则将边添加到结果集中,并使用并查集合并两个子集。 c. 如果两个端点在相同的子集中,说明添加该边会形成环,所以跳过这条边。
- 当最小生成树中的边数等于顶点数减1时,算法结束。
#include <stdio.h>
#include <stdlib.h>
// 定义边的结构体
typedef struct Edge {
int src, dest, weight;
} Edge;
// 定义图的结构体
typedef struct Graph {
int V, E;
Edge* edge;
} Graph;
// 定义并查集节点结构体
typedef struct Subset {
int parent, rank;
} Subset;
// 创建图
Graph* createGraph(int V, int E) {
// 为图分配内存
Graph* graph = (Graph*)malloc(sizeof(Graph));
graph->V = V;
graph->E = E;
// 为边分配内存
graph->edge = (Edge*)malloc(E * sizeof(Edge));
return graph;
}
// 查找
int find(Subset subsets[], int i) {
// 如果当前节点不是根节点,继续查找它的父节点
if (subsets[i].parent != i)
subsets[i].parent = find(subsets, subsets[i].parent);
// 返回根节点
return subsets[i].parent;
}
// 合并
void Union(Subset subsets[], int x, int y) {
// 查找 x 和 y 的根节点
int xroot = find(subsets, x);
int yroot = find(subsets, y);
// 比较 x 和 y 的根节点的秩
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
else {
// 如果它们的秩相等,将 y 的根节点作为 x 的根节点,并增加 x 的秩
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// 边比较函数,用于 qsort
int edgeCompare(const void* a, const void* b) {
Edge* e1 = (Edge*)a;
Edge* e2 = (Edge*)b;
return e1->weight > e2->weight;
}
// Kruskal 算法实现
void KruskalMST(Graph* graph) {
int V = graph->V;
Edge result[V]; // 存储最小生成树的边
int e = 0, i = 0;
// 对边进行排序
qsort(graph->edge, graph->E, sizeof(graph->edge[0]), edgeCompare);
// 为子集分配内存
Subset* subsets = (Subset*)malloc(V * sizeof(Subset));
// 初始化子集
for (int v = 0; v < V; ++v) {
subsets[v].parent = v;
subsets[v].rank = 0;
}
// 循环直到最小生成树包含 V-1 条边
while (e < V - 1 && i < graph->E) {
// 获取下一条最小边
Edge next_edge = graph->edge[i++];
// 查找该边的两个端点所属的子集
int x = find(subsets, next_edge.src);
int y = find(subsets, next_edge.dest);
// 如果两个端点不在同一个子集
if (x != y) {
// 将边添加到结果中
result[e++] = next_edge;
// 合并两个子集
Union(subsets, x, y);
}
}
// 输出构建的最小生成树的边
printf("Edges in the constructed MST\n");
for (i = 0; i < e; ++i)
printf("%d -- %d == %d\n", result[i].src, result[i].dest, result[i].weight);
// 释放子集内存
free(subsets);
}
int main() {
int V = 4;
int E = 5;
Graph* graph = createGraph(V, E);
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[0].weight = 10;
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
graph->edge[1].weight = 6;
graph->edge[2].src = 0;
graph->edge[2].dest = 3;
graph->edge[2].weight = 5;
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
graph->edge[3].weight = 15;
graph->edge[4].src = 2;
graph->edge[4].dest = 3;
graph->edge[4].weight = 4;
KruskalMST(graph);
return 0;
}
最短路径
在图的应用中,最短路径问题是一个经典问题,用于查找从一个顶点到另一个顶点的最短路径。最短路径问题有许多实际应用,如网络路由、地图导航、物流优化等。
最短路径问题概述
最短路径问题是寻找从一个顶点到另一个顶点的最短路径。在带权重的图中,最短路径是指权重之和最小的路径。最短路径问题有多种算法,下面将重点介绍Dijkstra算法和Floyd-Warshall算法。
Dijkstra算法
Dijkstra算法是一种解决单源最短路径问题的贪心算法,适用于带权重的有向图。该算法每次从未处理的顶点中选择距离源顶点最近的顶点,并更新其相邻顶点的距离。

实现步骤:
- 初始化:
- 创建一个顶点集合S,将源顶点V0加入其中;创建一个顶点集合T,包含除V0之外的所有顶点。
- 创建一个辅助数组D,用于存储源顶点V0到T中顶点的最短距离。
- 对于每个顶点Vi(i≠0),初始化D[i]的值:
- 如果<V0,Vi>存在(即两点间存在弧),则将D[i]设为权值;
- 否则,将D[i]设为 ∞ \infty ∞(表示V0不能直接抵达该顶点)
- 对于每个顶点Vi(i≠0),初始化D[i]的值:
- 迭代阶段:
- 在T中寻找距离V0最近的顶点Vmin(可以通过遍历D数组找到)。
- 将Vmin从T中移除并加入S中。
- 对于Vmin的每个相邻顶点Vadj的距离:new_distance=D[Vmin]+weight(Vmin,Vadj)。
- 如果new_distance小于D[Vadj],则更新D[Vadj]的值:D[Vadj]=new_distance。
- 如果T仍然为空,重复以上过程。
- 输出结果:
- 遍历D数组,打印源顶点V0到所有其他顶点的最短距离。
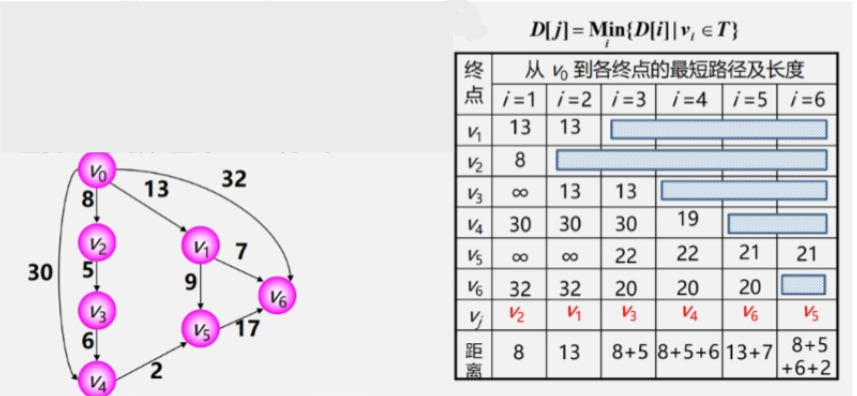
在迭代阶段,我们使用V0逐渐作为跳板,通过与S已有顶点连接,寻找最短的路径。此过程持续到所有顶点都被加入S中,意味着找到了从V0到所有顶点的最短路径。最后,输出结果即可。
#include <stdio.h>
#include <limits.h> // 引入 INT_MAX
// 图中顶点的数量
#define V 5
// 辅助函数:从尚未包含在最短路径树中的顶点集合中找到具有最小距离值的顶点
// 参数:
// dist[] - 存储从源顶点到其他顶点的最短距离的数组
// visited[] - 记录已访问过的顶点的数组
int min_distance(int dist[], int visited[]) {
int min = INT_MAX, min_index;
// 遍历所有顶点
for (int v = 0; v < V; v++) {
// 如果顶点尚未访问且距离小于当前最小距离,则更新最小距离
if (!visited[v] && dist[v] <= min) {
min = dist[v];
min_index = v;
}
}
// 返回具有最小距离值的顶点索引
return min_index;
}
// 函数:打印从源顶点到所有其他顶点的最短距离
// 参数:
// dist[] - 存储从源顶点到其他顶点的最短距离的数组
void print_solution(int dist[]) {
printf("顶点 \t 最短距离\n");
// 遍历所有顶点,打印其与源顶点的最短距离
for (int i = 0; i < V; i++) {
printf("%d \t %d\n", i, dist[i]);
}
}
// Dijkstra算法实现
void dijkstra(int graph[V][V], int src) {
int dist[V]; // 存储从源顶点到其他顶点的最短距离的数组
int visited[V]; // 记录已访问过的顶点
// 初始化
for (int i = 0; i < V; i++) {
dist[i] = INT_MAX;
visited[i] = 0;
}
// 将源顶点到自身的距离设为0
dist[src] = 0;
// 遍历所有顶点,更新距离值
for (int count = 0; count < V - 1; count++) {
// 从尚未处理的顶点中选择具有最小距离值的顶点
int u = min_distance(dist, visited);
// 将选中的顶点标记为已访问
visited[u] = 1;
// 更新与选中顶点相邻的顶点的距离值
for (int v = 0; v < V; v++) {
if (!visited[v] && graph[u][v] && dist[u] != INT_MAX && dist[u] + graph[u][v] < dist[v]) {
dist[v] = dist[u] + graph[u][v];
}
}
}
// 打印最终结果
print_solution(dist);
}
int main() {
// 示例图的邻接矩阵表示
int graph[V][V] = {
{0, 10, 0, 5, 0},
{0, 0, 1, 2, 0},
{0, 0, 0, 0, 4},
{0, 3, 9, 0, 2},
{7, 0, 6, 0, 0}
};
dijkstra(graph, 0);
return 0;
}
Floyd-Warshall算法
算法的核心思想:是逐个尝试添加中间顶点,看是否能够通过这个中间顶点缩短两个顶点之间的最短路径。
实现步骤:
- 初始化:创建一个n阶方针dist,其中n为顶点的数量。对角线元素初始化为0(表示从顶点到自身的距离),若两点之间存在边,则对应元素为边的权值;否则则为无穷大(通常表示一个很大的数,例如INT_MAX)。
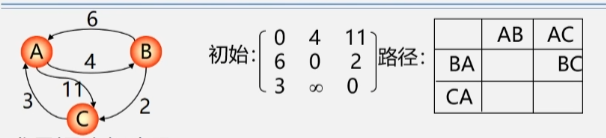
- 逐步添加中间顶点:遍历所有顶点k(1≤k≤n),对于每个顶点k,检查通过顶点k的路径是否能够缩短其他顶点对之间的距离。
- 对于每一对顶点 i 和 j(1≤i≤n,1≤j≤n),比较当前距离
dist[i][j]和通过顶点 k 的距离dist[i][k] + dist[k][j]。如果通过顶点k的距离更短了(即dist[i][k] + dist[k][j] < dist[i][j]),则更新dist[i][j]为新的较短路径(dist[i][j] = dist[i][k] + dist[k][j])。 - 在每次迭代中,都尝试使用一个新的中间顶点k来更新所有顶点对之间的最短路径。这样,当遍历完所有顶点后,我们就得到了包含所有中间顶点的最短路径。
- 对于每一对顶点 i 和 j(1≤i≤n,1≤j≤n),比较当前距离
- 结果输出:经过以上步骤,矩阵dist[i][j]中的元素表示顶点i到顶点j的最短路径长度。如果需要输出具体的最短路径,可以在更新最短路径时记录路径信息。
弗洛伊德算法的主要优势在于实现简单,适用于处理稠密图的情况。然而,需要注意的是,该算法不能处理存在负权环的图,因为在负权环中,存在无穷递减的路径。
代码实现:
#include <stdio.h>
#include <limits.h>
#define N 4 // 顶点的数量
#define INF INT_MAX // 用于表示无穷大(无法到达的情况)
void floyd(int graph[N][N], int dist[N][N]) {
// 初始化 dist 矩阵,将 graph 的权重复制到 dist 矩阵
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
dist[i][j] = graph[i][j];
}
}
// 逐步尝试添加中间顶点
for (int k = 0; k < N; k++) {
// 遍历所有顶点对 (i, j)
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
// 检查通过中间顶点k的路径是否比当前路径更短
if (dist[i][k] != INF && dist[k][j] != INF && dist[i][k] + dist[k][j] < dist[i][j]) {
// 更新最短路径
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
}
int main() {
// 输入的图的邻接矩阵表示
int graph[N][N] = {
{0, 5, INF, 10},
{INF, 0, 3, INF},
{INF, INF, 0, 1},
{INF, INF, INF, 0}
};
int dist[N][N]; // 存储最短路径的矩阵
// 调用 floyd 函数求解所有顶点对之间的最短路径
floyd(graph, dist);
// 输出最短路径矩阵
printf("最短路径矩阵:\n");
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (dist[i][j] == INF) {
printf("%7s", "INF");
} else {
printf("%7d", dist[i][j]);
}
}
printf("\n");
}
return 0;
}
Dijkstra算法和Floyd算法的对比
Dijkstra算法:
- 目的:Dijkstra算法用于求解单源最短路径问题,即从一个指定的起始顶点到图中其他所有顶点的最短路径。
- 思想:Dijkstra算法基于贪心策略,每次选择距离起始顶点最近的未访问顶点,然后更新通过该顶点到其他顶点的距离。
- 适用场景:Dijkstra算法适用于有向图和无向图,但不适用于存在负权边的图。
- 时间复杂度:使用优先队列实现时,时间复杂度为O((V+E)logV),其中V表示顶点数,E表示边数。
Floyd-Warshall算法:
- 目的:Floyd算法用于求解所有顶点对之间的最短路径问题。
- 思想:Floyd算法是一种动态规划方法,逐个尝试添加中间顶点,看是否能够通过这个中间顶点缩短两个顶点之间的最短路径。
- 适用场景:Floyd算法适用于有向图和无向图,但不适用于存在负权环的图。
- 时间复杂度:时间复杂度为O(V^3),其中V表示顶点数。
两者的优势:
- Dijkstra算法的优势:当我们只关心从某个特定顶点到其他所有顶点的最短路径时,Dijkstra算法是一个更高效的选择。对于稀疏图,Dijkstra算法的时间复杂度通常低于Floyd算法。
- Floyd算法的优势:Floyd算法可以求解所有顶点对之间的最短路径,适用于稠密图。此外,Floyd算法的实现相对简单,容易理解。
拓扑排序
有向无环图(DAG,Directed Acyclic Graph)是一种无环的有向图,常用于表示具有先后顺序关系的任务或事件。在这种图中,顶点代表任务或事件,而边表示任务或事件之间的依赖关系。根据表示子工程的方式,可以将其分为两类:AOV网和AOE网。
- AOV网(Activity On Vertex network):
- AOV网中,顶点表示活动或任务,边表示活动之间的优先制约关系。
- AOV网常用于拓扑排序,即对图中的顶点进行线性排序,使得对于任意一对顶点u和v,如果存在一条从u到v的有向边,那么u在排序中一定出现在v之前。拓扑排序可以帮助确定任务的执行顺序。
- AOE网(Activity On Edge network):
- AOE网中,边表示活动或任务,顶点表示活动的开始或结束事件。
- AOE网常用于关键路径分析,即找到工程中最长的路径,也就是工程的最短完成时间。关键路径上的活动是影响整个工程进度的关键活动,需要特别关注。
AOV网的特点
- 前驱和后继关系:在AOV网中,如果从顶点 i 到顶点 j 存在一条有向路径,那么 i 是 j 的前驱,而 j 是 i 的后继。这种关系表示 j 依赖于 i ,即在完成 j 之前必须先完成 i 。
- 直接前驱和直接后继关系:如果在AOV网中存在一条从顶点 i 到顶点 j 的有向边(即 i 和 j 之间的直接连接),那么 i 是 j 的直接前驱,而 j 是 i 的直接后继。这种关系表示 j 直接依赖于 i 的完成。
- 无环性:AOV网不允许存在回路。回路意味着某个活动或任务需要自身先完成才能开始,这在实际情况中是不合理的。例如,如果有一个回路包含课程C1、C2和C3,这意味着我们必须先完成C1才能开始C2,先完成C2才能开始C3,而先完成C3才能开始C1。这样的依赖关系是无法解决的,因此AOV网中不允许存在回路。
- 有序性:在AOV网中,可以通过拓扑排序为所有活动或任务确定一个执行顺序,使得在执行某个任务之前,它所依赖的所有任务都已完成。
拓扑排序的方法
拓扑排序是基于有向无环图(DAG)的性质,在保证DAG中所有依赖关系得到满足的前提下,对所有顶点进行线性排序。
算法思想:
-
顶点的选择:拓扑排序每次选择一个没有前趋的顶点作为输出。这样的顶点可以保证其所有的前驱节点已经被处理。
-
依赖关系的更新:每次输出一个顶点后,需要更新与其相关的依赖关系。具体而言,就是删除从该顶点发出的所有有向边,并检查这些边的终点是否变成了没有前趋的顶点。
-
环的检测:拓扑排序可以检测有向图中是否存在环。如果拓扑排序结果列表中的顶点数小于有向图中的顶点数,那么说明有向图中存在环。这是因为当存在环时,环中的顶点永远无法成为没有前趋的顶点。
代码实现
实现步骤
- 定义数据结构:定义一个有向图的数据结构,包含顶点和有向边。通常可以使用邻接矩阵或邻接表来表示有向图。
- 初始化图:创建一个图实例,将顶点和边的信息填充到图中。
- 计算入度:遍历图中的所有顶点,计算每个顶点的入度(指向该顶点的边的数量)。
- 寻找入度为0的顶点:遍历所有顶点,将入度为0的顶点放入一个集合(如栈或队列)中。
- 处理入度为0的顶点:当集合不为空时,执行以下操作:
- 从集合中移除一个入度为0的顶点。
- 将该顶点添加到拓扑排序结果列表中。
- 遍历从该顶点出发的所有有向边,将边从图中移除并更新对应顶点的入度。如果某个顶点的入度变为0,则将其添加到集合中。
- 检查结果:比较拓扑排序结果列表中的顶点数量与有向图中的顶点数量。如果它们相等,说明拓扑排序成功,输出拓扑序列。如果它们不等,说明有向图中存在环,拓扑排序失败。
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTEX 10
// 定义邻接矩阵
typedef struct {
int edges[MAX_VERTEX][MAX_VERTEX];
int vertexCount;
} Graph;
// 初始化图
void initGraph(Graph *graph, int vertexCount) {
graph->vertexCount = vertexCount;
for (int i = 0; i < vertexCount; ++i) {
for (int j = 0; j < vertexCount; ++j) {
graph->edges[i][j] = 0;
}
}
}
// 添加边
void addEdge(Graph *graph, int from, int to) {
graph->edges[from][to] = 1;
}
// 获取入度
void getIndegree(Graph *graph, int indegree[]) {
for (int i = 0; i < graph->vertexCount; ++i) {
indegree[i] = 0;
// 遍历所有顶点,统计顶点 i 的入度
for (int j = 0; j < graph->vertexCount; ++j) {
indegree[i] += graph->edges[j][i];
}
}
}
// 拓扑排序
int topologicalSort(Graph *graph, int sorted[]) {
int indegree[MAX_VERTEX]; // 入度数组
int stack[MAX_VERTEX]; // 栈
int stackTop = -1; // 栈顶指针
int sortedIndex = 0; // 已排序顶点计数
// 计算所有顶点的入度
getIndegree(graph, indegree);
// 将入度为 0 的顶点入栈
for (int i = 0; i < graph->vertexCount; ++i) {
if (indegree[i] == 0) {
stack[++stackTop] = i;
}
}
// 不断处理栈中的顶点
while (stackTop != -1) {
// 弹出栈顶顶点并将其加入排序结果
int current = stack[stackTop--];
sorted[sortedIndex++] = current;
// 遍历当前顶点的所有邻接点
for (int i = 0; i < graph->vertexCount; ++i) {
if (graph->edges[current][i] == 1) {
// 删除边
graph->edges[current][i] = 0;
// 更新入度
indegree[i]--;
// 如果入度变为 0,则入栈
if (indegree[i] == 0) {
stack[++stackTop] = i;
}
}
}
}
// 检查是否所有顶点都被处理
if (sortedIndex == graph->vertexCount) {
return 1;
} else {
return 0;
}
}
int main() {
Graph graph;
int sorted[MAX_VERTEX];
// 初始化图
initGraph(&graph, 6);
// 添加边
addEdge(&graph, 0, 2);
addEdge(&graph, 0, 3);
addEdge(&graph, 1, 3);
addEdge(&graph, 1, 4);
addEdge(&graph, 2, 3);
addEdge(&graph, 2, 5);
addEdge(&graph, 3, 5);
addEdge(&graph, 4, 5);
// 进行拓扑排序
if (topologicalSort(&graph, sorted)) {
printf("拓扑排序结果:");
for (int i = 0; i < graph.vertexCount; ++i) {
printf("%d ", sorted[i]);
}
printf("\n");
} else {
printf("拓扑排序失败,存在环。\n");
}
return 0;
}
检测AOV网中是否存在环的方法
在进行拓扑排序的过程中,如果有向图中存在环,那么拓扑排序是不能够完成的,即拓扑排序结果中的顶点数小于总顶点数。这是因为,当有向图中存在环时,环中的顶点之间相互约束,导致这些顶点的入度都无法减少到0。
在拓扑排序过程中,我们会不断寻找入度为0的顶点,然后将其加入排序结果,最后删除该顶点及其相关的边。如果一个顶点处于环中,那么在整个过程中,它的入度永远不会为0,因为它的前驱或后继顶点总是在约束它。在这种情况下,这个顶点不会被添加到拓扑排序结果中。
为了说明为什么后继顶点对环中顶点的约束不能被删除,我们可以举一个简单的例子。假设有一个有向图,包含三个顶点A、B和C,以及三条边:A->B,B->C和C->A。这是一个简单的环。在拓扑排序过程中,我们需要将环中的某个顶点及其相关的边删除,然后减少其后继顶点的入度。但是,在这个环中,每个顶点都是其他顶点的前驱和后继。因此,无论我们从哪个顶点开始,都无法删除与其相关的边。这就导致了拓扑排序无法完成,从而证明了有向图中存在环。
最短路径
用AOE网表示工程计划
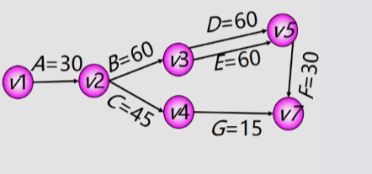
例:准备一个小型家庭宴会,晚上六点宴会开始,最迟几点开始准备?压缩哪项活动时间可以让总时间减少?
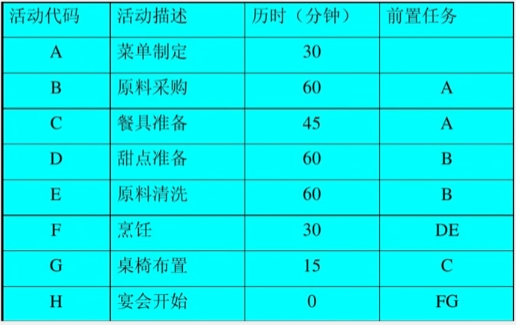
-
把工程计划表示为边表示活动的网络,即 AOE 网,用顶点表示事件,弧表示活动,弧的权表示活动持续时间。
-
事件
(顶点):表示在它之前的活动已经完成,在它之后的活动可以开始。
- 如:顶点 V2 表示 A 活动结束,BC 活动可以开始,顶点 V3 表示 活动 B 结束,DE 活动可以开始。
求解关键路径
设一个工程有 11 个活动,9 个事件。
- 事件 V1:表示整个工程开始(源点:入度为 0 的顶点)。
- 事件 V9:表示整个工程结束(汇点:出度为 0 的顶点)。
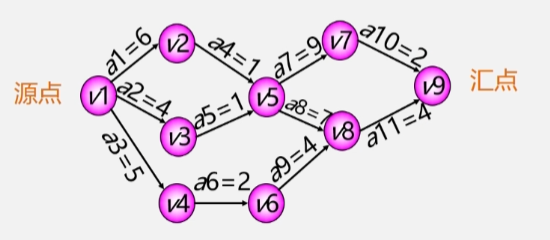
有了这样一个AOE网后,现在有两个问题:
- 完成整项工程至少需要多少时间?
- 关键路径的长度,就是整个工程至少需要的时间。
- z哪些活动是影响工程进度的关键?
- 关键路径上的这些活动就是影响工程进度的关键。
关键路径
- 从源点到汇点路径长度最长的路径。
路径长度
- 路径上各活动持续时间(权值)之和。
道理很简单,就是几个人同时到一个地方集合,离得近的到得早,离得远的到得晚,但只有最晚到的人到了,大家才算凑到一块了。
确定关键路径
为了确定关键路径,需要定义 4 个描述量:
假设所有活动全部完成需要消耗 180 分钟
- ve(vj):关于顶点的,表示事件 vj 的最早发生时间。
- vl(vj):关于顶点的,表示事件 vj 的最迟发生时间。
- e(i):表示活动 ai 的最早开始时间。
- l(i):表示活动 ai 的最晚开始时间。
关键活动:没有时间余量的活动,关键路径上的路径,即 l(i) = e(i)(即 l(i) - e(i) = 0)的活动。由若干个关键活动所组成的路径就是关键路径。
如何找l(i) == e(i) 的关键活动?
设活动 ai 用弧 <j , k> 表示,其持续时间记为:Wj,k,则有:
e(i) = ve(j) l(i) = vl(k) - Wj,k
如何求 ve(j) 和 vl(j)?
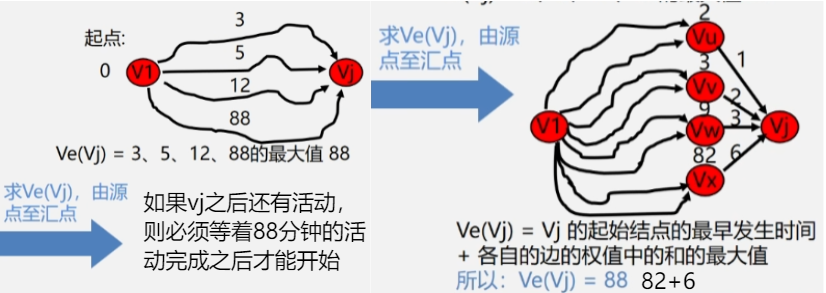
- 求最早发生时间:从 ve(1) = 0开始向前递推 ve(j) = Max{ve(i) + Wi,j},< i,j > ∈ T,2 <= j <= n。其中 T 是所有以 j 为头的弧的集合。 从源点到某个顶点的全部路径中,选择路径长度(权值和)最大的那条路。
- 求最晚发生时间:从 vl(n) = ve(n) 开始向后递推。 vl(i) = Min{vl(j) - Wi,j},< i,j > ∈ S,1 <= i <= n-1。其中 S 是所有以 i 为尾的弧的集合。 Vi 顶点后继的那个顶点Vj的最迟发生时间减去Vi与Vj之间弧的权值。
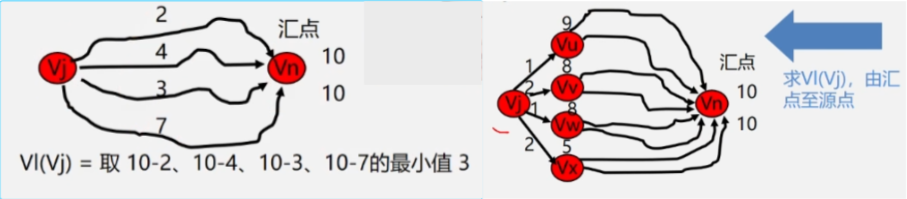
找顶点 vj 的最早发生时间的方法是从源点到某个顶点的全部路径中,选择路径长度(权值和)最大的那条路。而找顶点 vj 的最迟结束时间的方法是后面的顶点减去前面的顶点之间的弧的权值,取差的最小值就是Vj的最迟发生时间。
通过这些步骤,我们可以找到关键活动和关键路径,从而确定项目的关键路径。
求关键路径步骤
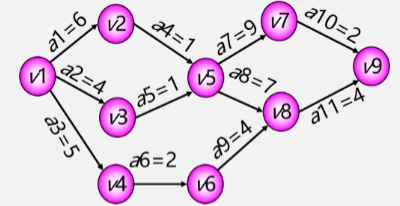
求关键路径的步骤如下:
- 求各个顶点事件的最早发生时间 ve(i) 和最迟发生时间 vl(j)。

- 求活动的最早开始时间 e(i) 和最晚开始时间 l(i):
- e(i) = ve(j):活动的最早发生时间等于对应顶点事件的最早发生时间。
- l(i) = vl(k) - Wj,k:活动的最晚开始时间等于对应顶点事件的最迟发生时间减去活动的持续时间。
- 计算活动的时间差 l(i) - e(i):
- 差值为 0 的活动是关键活动。
- 由若干个关键活动所组成的路径就是关键路径。
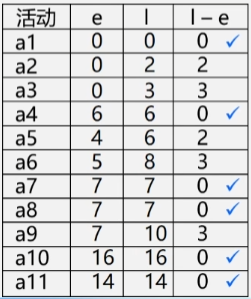
通过这些步骤,我们可以找到关键路径,如 a1 a4 a7 a8 a10 a11。
关键路径的讨论: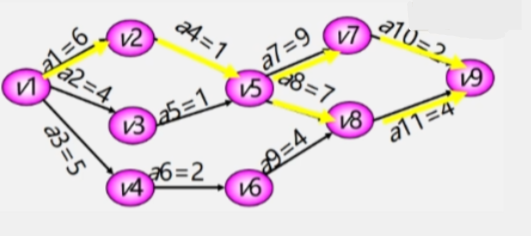
- 如果网络中有几条关键路径,则需要加快同时在几条关键路径上的关键活动。例如:a11、a10、a8、a7。
- 如果一个活动处于所有的关键路径上,那么提高这个活动的速度就能缩短整个工程的完成时间。例如:a1、a4。
- 处于所有关键路径上的活动完成时间不能缩短太多,否则会使原来的关键路径变成不是关键路径。这时,必须重新寻找关键路径。例如:如果 a1 的完成时间由 6 天变成 3 天,就会改变关键路径。
代码实现
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX 100
#define INFINITY 0x3f3f3f3f
//define the struct of the vertex
typedef struct Vertex {
int ve, vl; // the earliest time and the latest time
} Vertex;
// define the struct of the edge
typedef struct Edge {
int from, to, weight; // the start vertex, the end vertex and the weight(time)
} Edge;
int n, m; //the number of the vertex and the edge
Vertex vertex[MAX]; // the array of the vertex
Edge edges[MAX]; // the array of the edge
int indegree[MAX]; // the array of the indegree of the vertex
int outdegree[MAX]; // the array of the outdegree of the vertex
int topo[MAX], topo_index; // the topological sort results and indexs
// topological sort
int topological_sort() {
int queue[MAX], head = 0, tail = 0; // the queue of the vertex
int i; // the index of the vertex
// initialize the queue with the vertex whose indegree is 0
for (i = 1; i <= n; ++i) {
if (indegree[i] == 0) {
queue[tail++] = i; // enqueue
}
}
// topological sort
while (head < tail) {
int u = queue[head++]; // dequeue a one vertex
topo[topo_index++] = u; // add the vertex to the topological sort results
// from the vertex u, traverse all the vertex v
for (i = 0; i < m; ++i) {
if (edges[i].from == u) {
int v = edges[i].to; // the vertex v is the end vertex of the edge (u,v)
indegree[v]--; // the indegree of the vertex v minus 1
if (indegree[v] == 0) {
queue[tail++] = v; // if the indegree of the vertex v is 0, enqueue the vertex v
}
}
}
}
// if the number of sorted vertex is equal to the number of the vertex , the topological sort is successful
return topo_index == n;
}
// find the critical path
void critical_path() {
int i; // the index of the vertex
// initialize the earliest time of the vertex
for (i = 1; i <= n; ++i) {
vertex[i].ve = 0;
}
// find the earliest time of all the vertex
for (i = 0; i < n; ++i) {
int u = topo[i]; // the vertex u is the i-th vertex in the topological sort results
for (int j = 0; j < m; ++j) {
if (edges[j].from == u) {
int v = edges[j].to; // the vertex v is the end vertex of the edge (u,v)
int weight = edges[j].weight; // the weight of the edge (u,v)
// update the earliest time of the vertex v
if (vertex[v].ve < vertex[u].ve + weight) {
vertex[v].ve = vertex[u].ve + weight;
}
}
}
}
// initialize the latest time of the vertex
for (i = 1; i <= n; ++i) {
vertex[i].vl = vertex[n].ve;
}
// find the latest time of all the vertex
for (i = n - 1; i >= 0; --i) {
int u = topo[i]; // the vertex u is the i-th vertex in the topological sort results
for (int j = 0; j < m; ++j) {
if (edges[j].to == u) {
int v = edges[j].from; // the vertex v is the start vertex of the edge (v,u)
int weight = edges[j].weight; // the weight of the edge (v,u)
// update the latest time of the vertex v
if (vertex[v].vl > vertex[u].vl - weight) {
vertex[v].vl = vertex[u].vl - weight;
}
}
}
}
//print the critical path
printf("The critical path is:\n");
for (i = 0; i < m; ++i) {
int u = edges[i].from; // the vertex u is the start vertex of the edge (u,v)
int v = edges[i].to; // the vertex v is the end vertex of the edge (u,v)
int weight = edges[i].weight; // the weight of the edge (u,v)
int e = vertex[u].ve; // the earliest time of the vertex u
int l = vertex[v].vl - weight; // the latest time of the vertex v
// if the earliest time of the vertex u plus the weight of the edge (u,v) is equal to the latest time of the vertex v
// the edge (u,v) is the critical edge
if (vertex[u].ve + weight == vertex[v].vl) {
printf("%d->%d\n", u, v);
}
}
}
int main() {
printf("关键路径计算示例\n");
// 输入顶点数和边数
n = 7;
m = 9;
// 输入边信息
int input_edges[][3] = {
{1, 2, 6},
{1, 3, 4},
{1, 4, 5},
{2, 5, 1},
{3, 5, 1},
{4, 6, 2},
{5, 7, 9},
{6, 7, 7},
{4, 5, 3},
};
// 将边信息存入边数组
for (int i = 0; i < m; ++i) {
edges[i].from = input_edges[i][0];
edges[i].to = input_edges[i][1];
edges[i].weight = input_edges[i][2];
indegree[edges[i].to]++;
outdegree[edges[i].from]++;
}
// 拓扑排序
if (!topological_sort()) {
printf("存在环,无法进行拓扑排序\n");
return 1;
}
// 求关键路径
critical_path();
return 0;
}
//
// int main() {
// // 读取顶点数和边数
// printf("请输入顶点数和边数:");
// scanf("%d%d", &n, &m);
//
// // 读取各边信息
// printf("请输入各边的起点、终点和权重:\n");
// for (int i = 0; i < m; ++i) {
// scanf("%d%d%d", &edges[i].from, &edges[i].to, &edges[i].weight);
// indegree[edges[i].to]++;
// outdegree[edges[i].from]++;
// }
//
// // 拓扑排序
// if (!topological_sort()) {
// printf("存在环,无法进行拓扑排序\n");
// return 1;
// }
//
// // 求关键路径
// critical_path();
//
// return 0;
// }





![[NISACTF 2022]level-up](https://img-blog.csdnimg.cn/68fbfe3bbfe64cb190a03defc7959db9.png)