这是一篇关联规则挖掘的综述,也记录下自己的心得笔记
A comprehensive review of visualization methods for association rule mining: Taxonomy, Challenges, Open problems and Future ideas
文章目录
- 摘要
- 1、介绍
- 2、关联规则挖掘是个小东西
- 2.1、数值关联规则挖掘
- 2.2、时间序列关联规则挖掘
- 3、关联规则挖掘的可视化
- 参考
摘要
关联规则挖掘是为了搜索事物数据库中属性之间的关系。规则发现的整个过程非常复杂,包括预处理技术、规则挖掘步骤和后处理,其中进行了可视化处理。发现的关联规则的可视化是整个关联规则挖掘管道中的一个重要步骤,以加强用户对规则挖掘结果的理解。
在过去的几十年中,已经开发了一些关联规则挖掘和可视化的方法。本文旨在建立一个文献综述,确定发表在同行评议文献中的主要技术,研究每种方法的主要特征,并介绍该领域的主要应用。确定该研究领域的未来步骤是本评论文章的另一个目标。
1、介绍
背景比较悠远,出名的算法有Apriori,这个算法像基石一样。一般是分三步走:预处理、关联规则挖掘、后处理。这篇文章强调了可视化的好处。(ARM 就是关联规则挖掘的意思,Association Rule Mining)
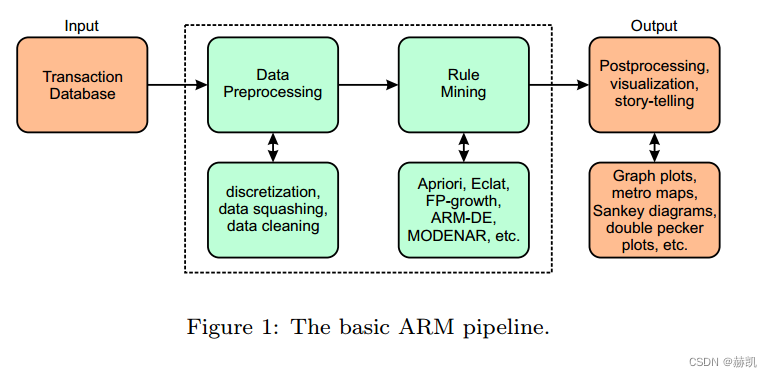
- 介绍了ARM可视化方法的演变。
- 定义了每种方法的特点。
- 概述了每种方法的优势/劣势。
- 对所调查的每种方法都提出了一个例子。
- 总结了使用ARM可视化的解释模型。
2、关联规则挖掘是个小东西
对规则关联挖掘的一些数学公式进行定义,现有有一个事物数据库,纵列是事物的指标,横行是不同的事物累计起来,也就是我们常见的数据库。规则挖掘就是看看事物不同指标之间的关系。
X⇒ Y,这个就是关联规则,指标集合X可以推出指标集合Y,它们之间没有交集,都属于数据库中的指标。
n代表后面的指标出现的次数,N代表一共有多少个事物,也就是数据库有多少行。
| 公式 | 名字 | 概率解释 |
|---|---|---|
| s u p p ( X ⇒ Y ) = n ( X ⋂ Y ) N supp(X⇒Y)=\frac{n(X\bigcap Y)}{N} supp(X⇒Y)=Nn(X⋂Y) | 支持度 | 这个规则出现的概率 |
| c o n f ( X ⇒ Y ) = n ( X ⋂ Y ) n ( X ) conf(X⇒Y)=\frac{n(X\bigcap Y)}{n(X)} conf(X⇒Y)=n(X)n(X⋂Y) | 置信度 | 在规则X出现的情况下,规则集合Y出现概率。也就是条件概率 |
| l i f t ( X ⇒ Y ) = s u p p ( X ⋂ Y ) s u p p ( X ) × s u p p ( Y ) lift(X⇒Y)=\frac{supp(X\bigcap Y)}{supp(X)\times supp(Y)} lift(X⇒Y)=supp(X)×supp(Y)supp(X⋂Y) | 提升度 | 规则X出现对规则Y出现概率的提升程度 |
| c o n v ( X ⇒ Y ) = 1 − s u p p ( Y ) 1 − c o n f ( X ⇒ Y ) conv(X⇒Y)=\frac{1-supp(Y)}{1-conf(X⇒Y)} conv(X⇒Y)=1−conf(X⇒Y)1−supp(Y) | 出错度 | 判断这个规则出错的概率, |
一般会定义 s u p p ( X ⇒ Y ) ≥ S m i n supp(X ⇒ Y ) ≥ Smin supp(X⇒Y)≥Smin , c o n f ( X ⇒ Y ) ≥ C m i n conf (X ⇒ Y ) ≥ Cmin conf(X⇒Y)≥Cmin .其中 S m i n Smin Smin, C m i n Cmin Cmin是我们人为定下的阈值,超过这个阈值的关联规则才进行下一步考虑。
提升度表示含有X的条件下,同时含有Y的概率,与只看Y发生的概率之比。提升度反映了关联规则中的X与Y的相关性,提升度>1且越高表明正相关性越高,提升度<1且越低表明负相关性越高,提升度=1表明没有相关性,即相互独立 ,一般在数据挖掘中当提升度大于3时,我们才承认挖掘出的关联规则是有价值的。
PS. 在翻了一些别的资料,常用的判断方法还有KULC度量和不平衡比。
KULC就是两个置信度的平均值:
0.5
∗
(
c
o
n
f
(
X
⇒
Y
)
+
c
o
n
f
(
Y
⇒
X
)
)
0.5*(conf(X⇒Y)+conf(Y⇒X))
0.5∗(conf(X⇒Y)+conf(Y⇒X))
IR不平衡比例:
I
R
(
X
,
Y
)
=
∣
s
u
p
p
(
X
)
−
s
u
p
p
(
Y
)
∣
s
u
p
p
(
X
)
+
s
u
p
p
(
Y
)
−
s
u
p
p
(
X
⇒
Y
)
IR(X, Y) =\frac{|supp(X)-supp(Y)|}{supp(X)+supp(Y)-supp(X⇒Y) }
IR(X,Y)=supp(X)+supp(Y)−supp(X⇒Y)∣supp(X)−supp(Y)∣
KULC度量越大越好,IR不平衡比例越小越好,两者组合使用比单独使用Lift能更好的的发现强关联规则。
2.1、数值关联规则挖掘
通过上面的总结也看出来,这个只能离散化数据,有或者没有。但是现实生活中都是连续数字,一个指标可能从0~100这样。出来一个扩展(NARM,Numerical Association Rule Mining)数值关联规则挖掘。
在NARM中,每个数值属性都由可行值的区间限制,这个区间由属性的上下界确定。当挖掘的关联规则越多时,这个区间就越宽。相反,这个区间越窄,就能够发现属性之间更具体的关系。引入可行值区间有两个主要影响:将现有的离散搜索空间转换为连续空间,并更好地适应感兴趣的问题。挖掘出来的关联规则可以根据几个标准进行评估,如支持度和置信度。然而,对于NARM来说,必须考虑额外的措施,以便正确评估挖掘出来的关联规则集。
2.2、时间序列关联规则挖掘
TS-ARM是一种新的范式,它将交易数据库视为时间序列数据。NARM问题的正式定义需要根据这一点来重新定义。在TS-ARM中,关联规则被定义为一个公式:
X ( ∆ t ) ⇒ Y ( ∆ t ) X(∆t)⇒ Y(∆t) X(∆t)⇒Y(∆t)
∆ t = [ t 1 , t 2 ] ∆t=[t_1, t_2] ∆t=[t1,t2],其中 t 1 t_1 t1是开始时间、 t 2 t_2 t2是结束时间,我可以理解成 X ( ∆ t ) , Y ( ∆ t ) X(∆t),Y(∆t) X(∆t),Y(∆t)是在时间段内表现的事物序列。
c o n f t ( X ( ∆ t ) ⇒ Y ( ∆ t ) ) = n ( X ( ∆ t ) ∩ Y ( ∆ t ) ) n ( X ( ∆ t ) ) conft(X(∆t) ⇒ Y (∆t)) = \frac{n(X(∆t) ∩ Y (∆t))}{n(X(∆t))} conft(X(∆t)⇒Y(∆t))=n(X(∆t))n(X(∆t)∩Y(∆t)) 置信度
s u p p t ( X ( ∆ t ) ⇒ Y ( ∆ t ) ) = n ( X ( ∆ t ) ∩ Y ( ∆ t ) ) N ( ∆ t ) suppt(X(∆t) ⇒ Y (∆t)) =\frac{ n(X(∆t) ∩ Y (∆t))}{N(∆t)} suppt(X(∆t)⇒Y(∆t))=N(∆t)n(X(∆t)∩Y(∆t)) 支持度
上面两个式子表在在同一段时间内表现得置信度和支持度,就是把里面的数据换了一下。
3、关联规则挖掘的可视化
…
接下来就是这个文章就是研究针对不同问题哪种可视化最合适,略了

参考
https://cs.nyu.edu/~jcf/classes/g22.3033-002/slides/session6/MiningFrequentPatternsAssociationAndCorrelations.pdf