资源地址：

30基于非对称纳什谈判的多微网电能共享运行优化策略MATLAB程序资源-CSDN文库

参考文献：

《基于非对称纳什谈判的多微网电能共享运行优化策略》——吴锦领

仿真平台：MATLAB CPLEX+MOSEK/IPOPT

主要内容：

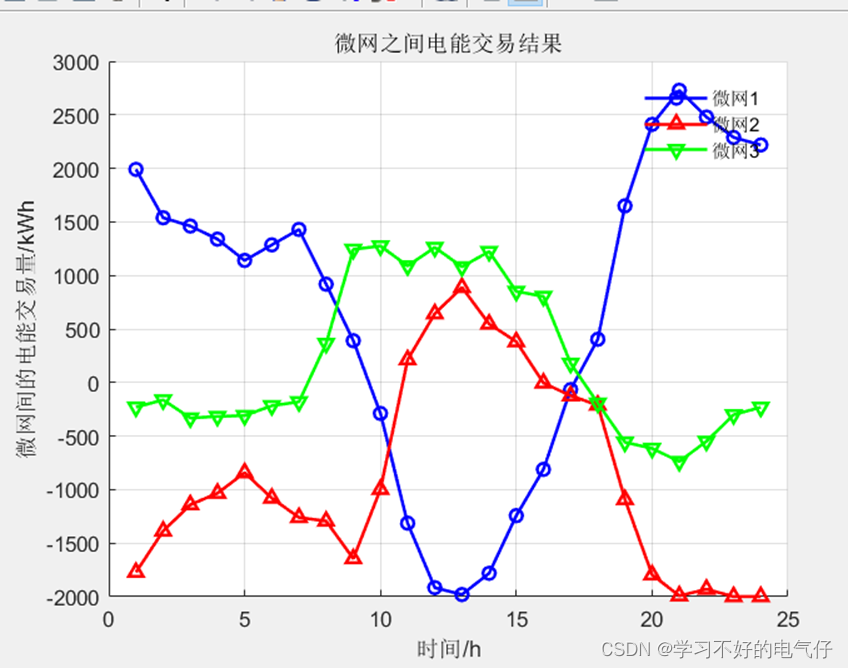
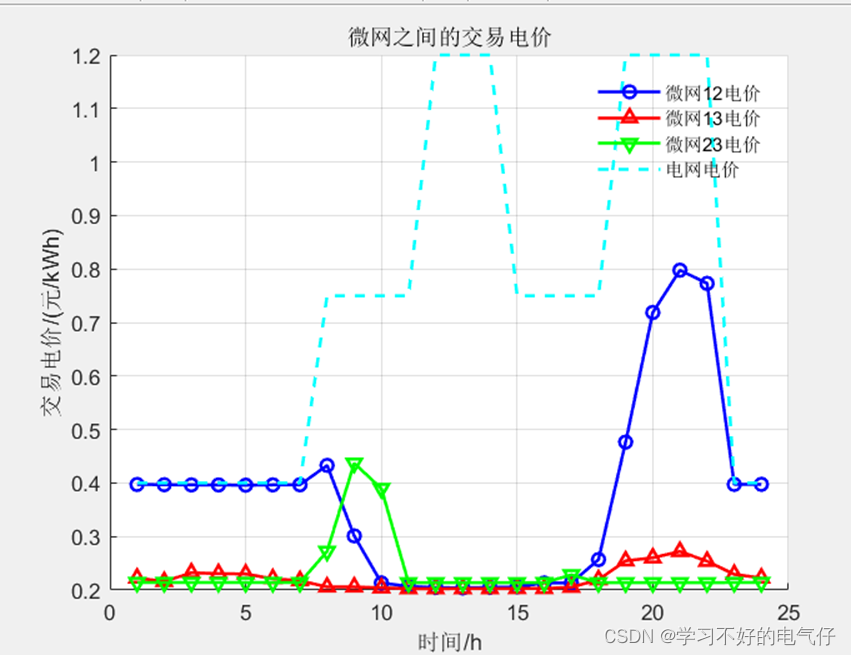
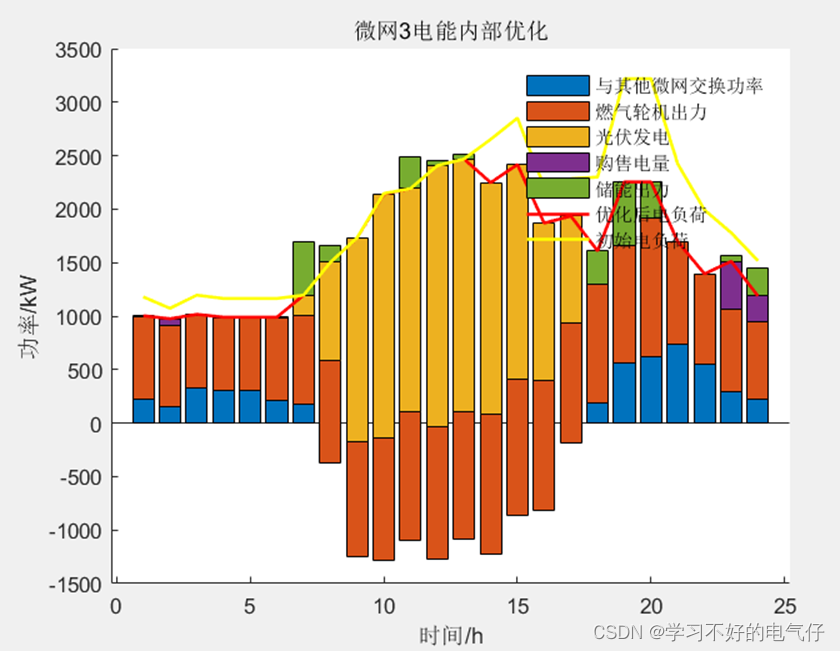
主要做的是微网间基于非对称纳什谈判的P2P电能交易共享问题，基于纳什谈判理论建立了多微网电能共享合作运行模型，进而将其分解为微网联盟效益最大化子问题和合作收益分配子问题，选择交替方向乘子法分布式求解，从而有效保护各主体隐私。在合作收益分配子问题中，提出以非线性能量映射函数量化各参与主体贡献大小的非对称议价方法，各微网分别以其在合作中的电能贡献大小为议价能力相互谈判，以实现合作收益的公平分配。同时，微电网模型中考虑了电转气以及碳捕集设备，实现了低碳调度。

部分程序：

%% 约束条件
C=[];
%微网的电/热负荷需求响应部分
for t=1:24
    C=[C,
       L_e(t)==L_e0(t)+P_e_cut(t)+P_e_tran(t), %微网的电负荷功率平衡约束
       L_h(t)==L_h0(t)-P_h_DR(t), %微网的热负荷功率平衡约束
       -0.15*L_e0(t)<=P_e_cut(t)<=0, %微网的可削减电功率上下限约束
       -0.15*L_e0(t)<=P_e_tran(t)<=0.15*L_e0(t), %微网的可转移电功率上下限约束
       0<=P_h_DR(t)<=0.2*L_h0(t), %微网的可削减热功率上下限约束
      ];
end
C=[C,sum(P_e_tran)==0,]; %转移的电负荷总量为0约束
%微网的储电设备约束部分
%储能电站荷电状态连续性约束
C=[C,E_bat(1)==800+0.95*P_batc(1)-P_batd(1)/0.96,]; %1时段约束
for t=2:24
    C=[C,E_bat(t)==E_bat(t-1)+0.95*P_batc(t)-P_batd(t)/0.96,]; %储电设备容量变化约束
end
%储能容量大小约束
for t=1:24
    C=[C,500<=E_bat(t)<=1800,];  %储电量上下限约束
end
%始末状态守恒
C=[C,E_bat(24)==800,];
%储能电站的充放电功率约束,Big-M法进行线性化处理
M=800; %这里的M是个很大的数
for t=1:24
    C=[C,
       0<=P_batc(t)<=500,
       0<=P_batc(t)<=U_abs(t)*M,     
       0<=P_batd(t)<=600,      
       0<=P_batd(t)<=U_relea(t)*M,
       U_abs(t)+U_relea(t)<=1,
      ];
end
%CHP机组以及GB等设备运行约束
for t=1:24
    C=[C,
       P_h_GT(t)==(1-0.35)/0.35*0.83*P_e_GT(t), %燃气轮机热电联产功率约束
       0<=P_e_GT(t)<=5000, %燃气轮机发电功率上下限约束
       0<=P_h_GB(t)<=800, %余热锅炉产热功率上下限约束
       0<=P_e_wd(t)<=Predict_wd(t), %风力发电上下限约束
      ];
end
for t=1:24
    C=[C,
       P_e_GT(t)+P_e_wd(t)+P_buy(t)+P_batd(t)==P_batc(t)+L_e(t)+P_sell(t),
       P_h_GT(t)+P_h_GB(t)==L_h(t),
      ];
end

输出结果：