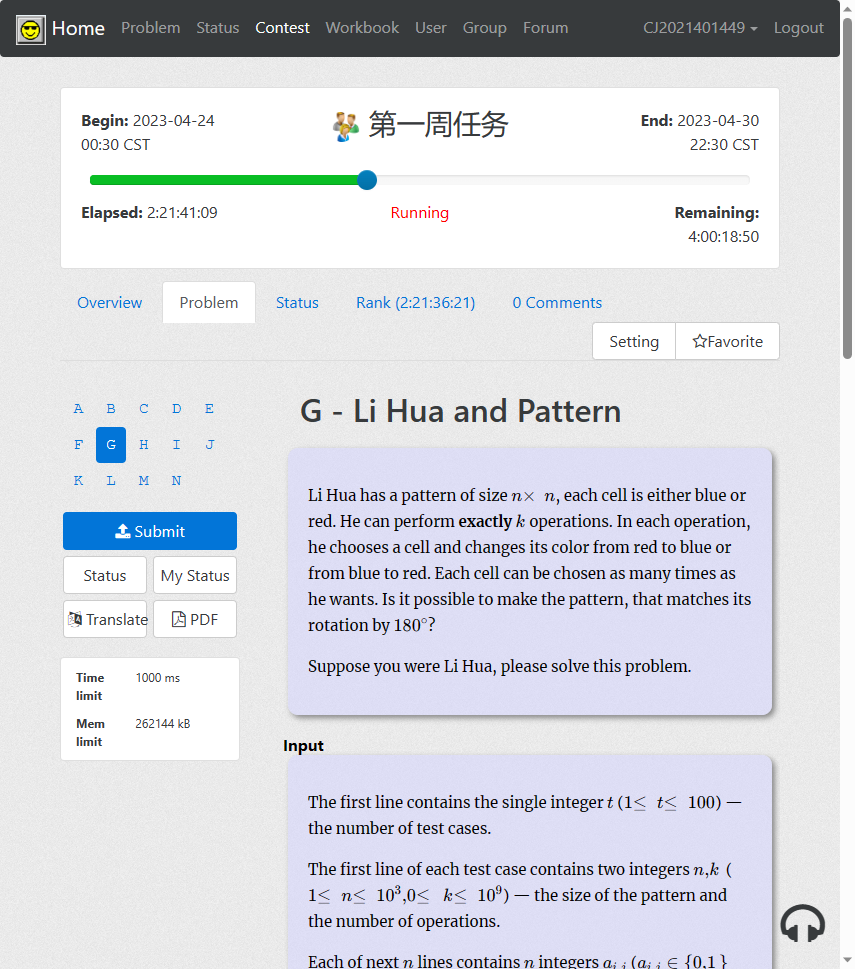
题意：给出了矩阵，里面每个位置分为蓝色或红色（数据上用1和0体现了），给出了一个操作次数，每次可以改变一个坐标的颜色，问能否通过操作使得图像旋转180度后不变。

解：很容易想到，需要使该图像中心对称，应该对称相等的两个位置不相等时，就需要进行一次操作，把其中一个修改成另一个颜色，我在输入这个操作时就计算出了需要修改的次数

cnt=0;
if(n%2==0)
   cen=n/2;
else
   cen=n/2+1;
for(int i=1; i<=n; i++)
   for(int j=1; j<=n; j++)
   {
      cin>>a[i][j];
      if(i>cen || (i==cen && j>cen && n%2==1))
        if(a[i][j]!=a[n-i+1][n-j+1])cnt++;
   }

但一开始忽略了很重要的一点，我没完全看明白的题意，

算出需要操作的次数后我就直接把所给操作次数与之相比较

如果次数够了就YES，不够就NO

结果答案错误给我整麻了

然后才发现题目要求给出的这个操作次数是要用完的！！

理解到这个意思那就好做了

先要计算出多出来的次数cnt

当cnt>0时

如果图像n*n的奇数长度的边，那么它最中间那个位置和它自己中心对称，无需考虑是什么颜色，那么不管还需要操作多少次都可以直接操作它消耗掉

但是如果是偶数长度的边，如果多出来奇数次操作数就会使得最后一次操作不得不打破原本的对称状态。

所以说，对此进一步作出判断就行了。

此题：

#include<bits/stdc++.h>
using namespace std;
int t,n,k,cnt,cen,a[1005][1005];
int main()
{
    cin>>t;
    while(t--)
    {
        cnt=0;
        cin>>n>>k;
        if(n%2==0)
            cen=n/2;
        else
            cen=n/2+1;
        for(int i=1; i<=n; i++)
            for(int j=1; j<=n; j++)
            {
                cin>>a[i][j];
                if(i>cen || (i==cen && j>cen && n%2==1))
                    if(a[i][j]!=a[n-i+1][n-j+1])cnt++;
            }
        //cout<<"有"<<cnt<<"次修改"<<endl;
        if(cnt>k)
        {
            cout<<"NO"<<endl;
            continue;
        }
        cnt=k-cnt;//多出来的次数
        //cout<<"多出了"<<cnt<<"次"<<endl;
        if(n%2==0 && cnt%2==1)
            cout<<"NO"<<endl;
        else
            cout<<"YES"<<endl;
    }
    return 0;
}