目录

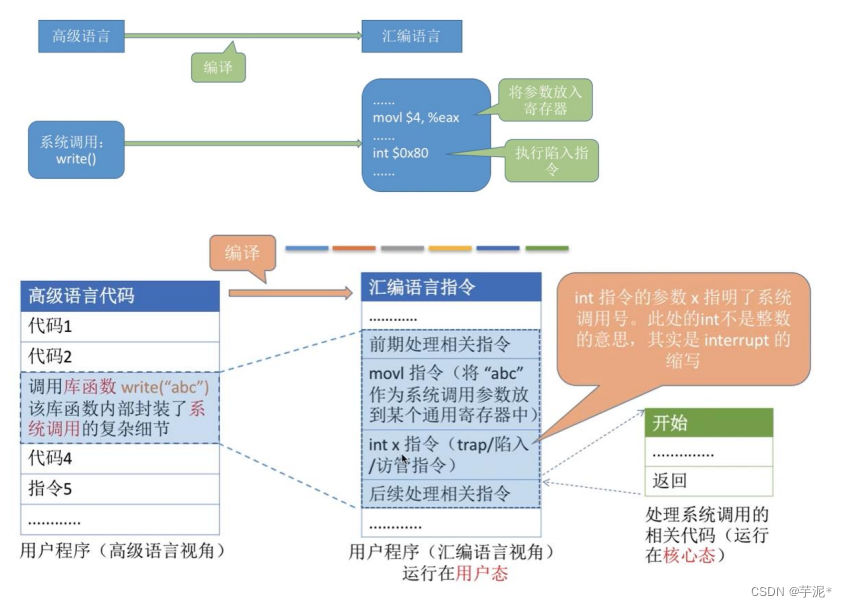
基本介绍

右单旋

左单旋

左右双旋

右左双旋 

平衡因子的计算

---

基本介绍

首先，平衡二叉树也是一棵二叉搜索树。

当我们在一棵平衡二叉树进行插入或者删除时，可能会把原来的平衡二叉树变得不平衡，

这个时候我们就需要进行调整了。

平衡二叉树的调整主要分为四大类：

• RR旋转（右单旋）
• LL旋转（左单旋）
• RL旋转（右左双旋）
• LR旋转（左右双旋）

右单旋

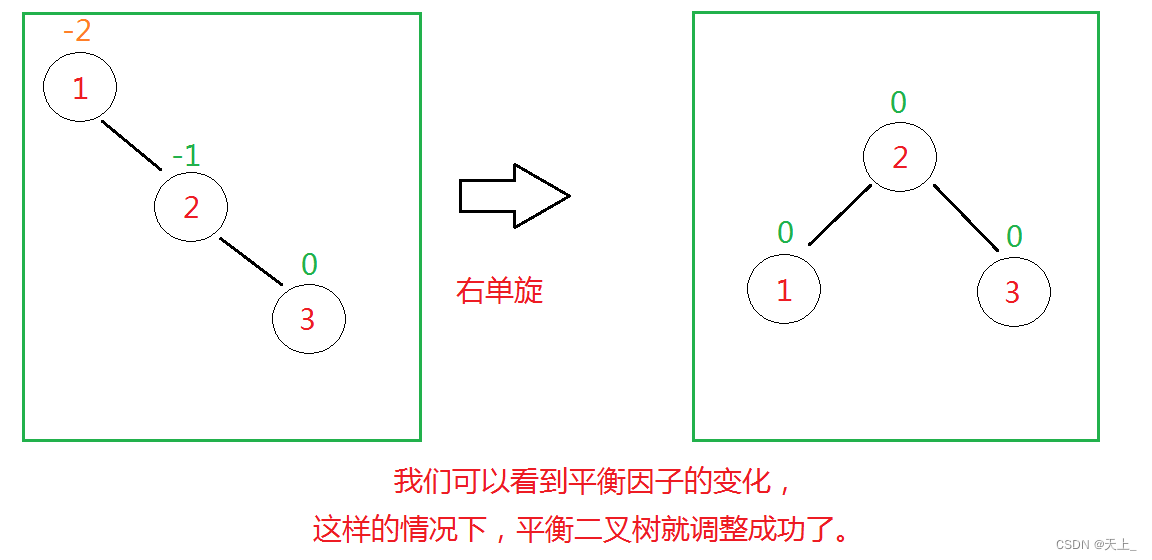
我们抽象化出两个概念：“发现者”、“麻烦结点”。 （或者说“被破坏者”和“破坏者”）

不平衡的“发现者”是1，“麻烦结点”为破坏了平衡的节点。

“麻烦结点”3在“发现者”右子树的右子树上，因而叫RR插入，需要RR旋转（右单旋）。

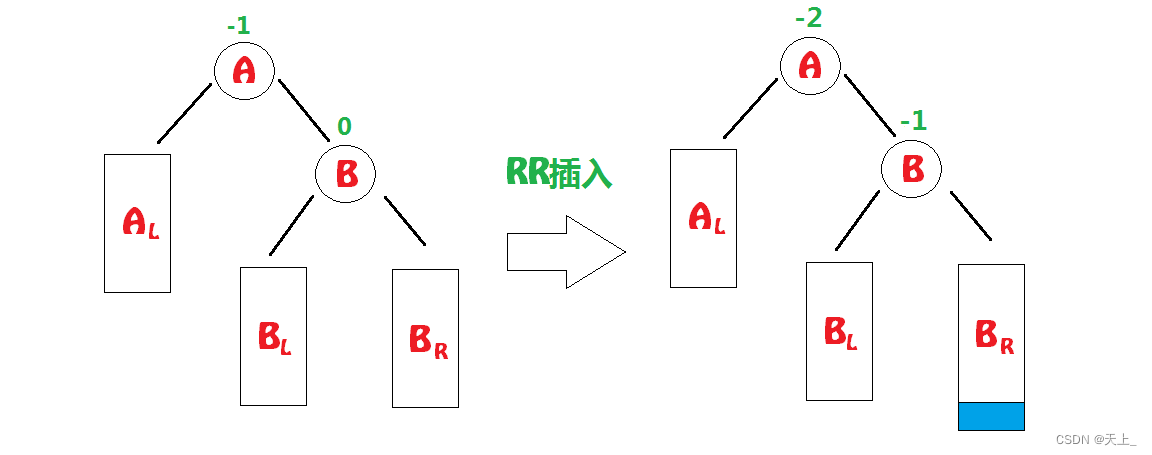
要注意的是：

插入到蓝色区域时，插入到其左子树或者右子树，处理方式都是一致的。

当发生了RR插入时，我们要进行RR旋转（右单旋）：

把B拎上来，且因为平衡二叉树也是二叉搜索树，要比B小，比A大，所以要放在B的左子树、A的右子树上。

左单旋

 

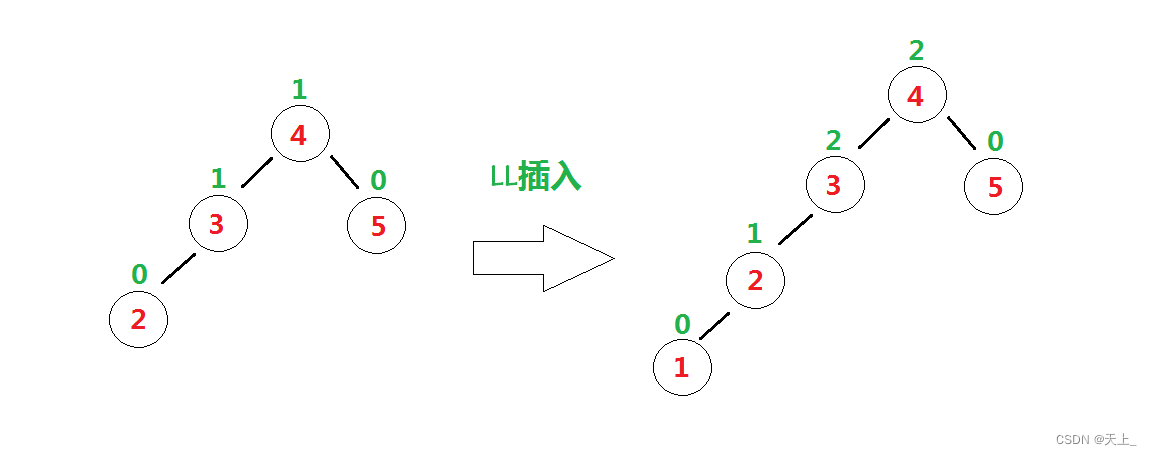
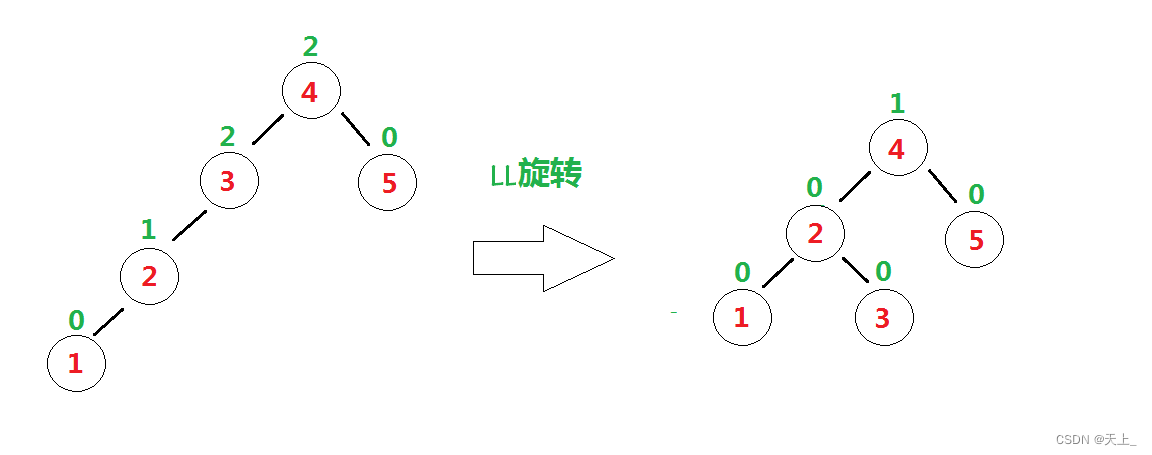
“发现者”是结点3，“麻烦结点”1在“发现者”左子树的左子树上。

故而需要进行LL旋转（左单旋） 

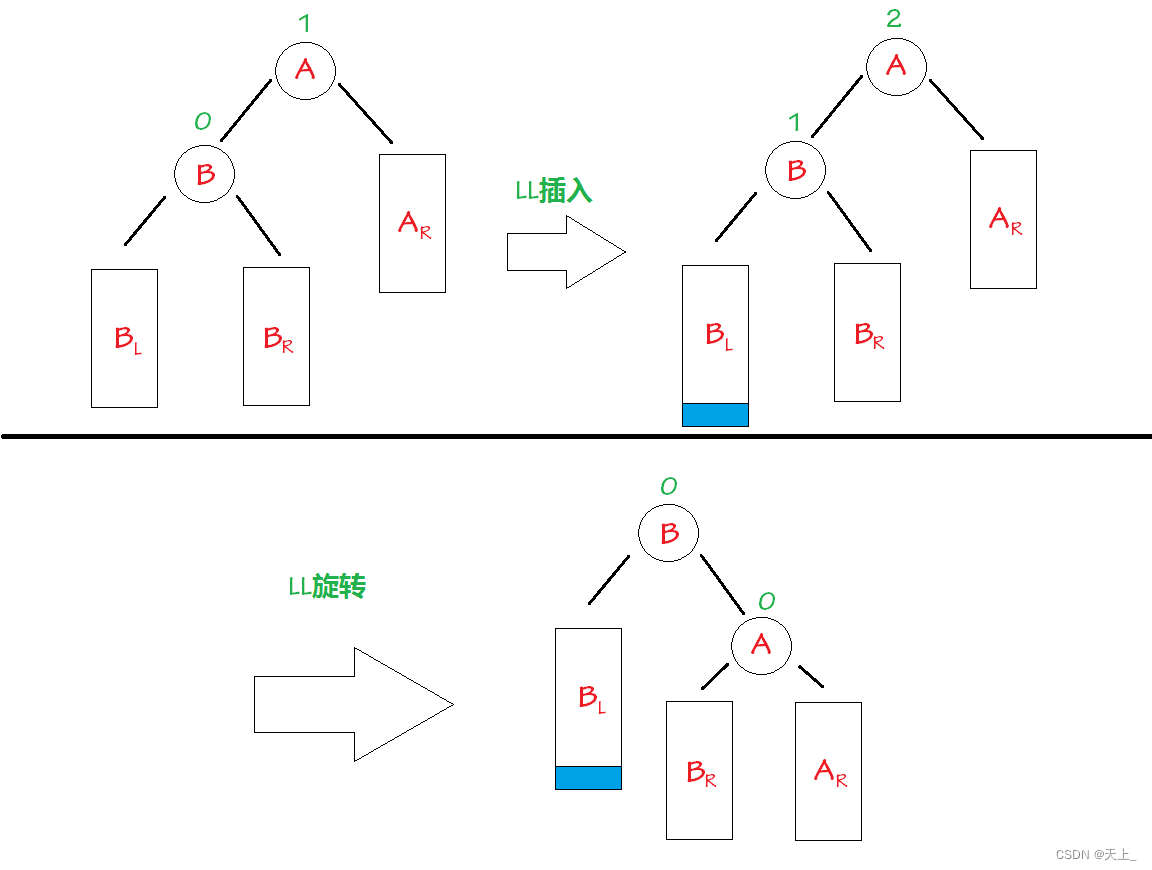
左右双旋

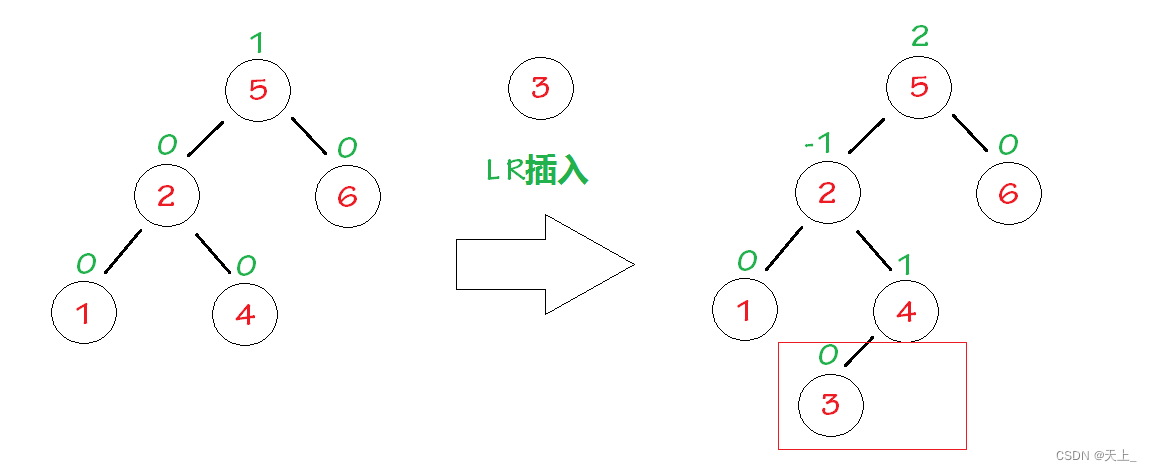
“发现者”是结点5，“麻烦结点”3在“发现者”左子树的右子树上，因而叫LR插入，需要进行LR旋转（左右双旋）。

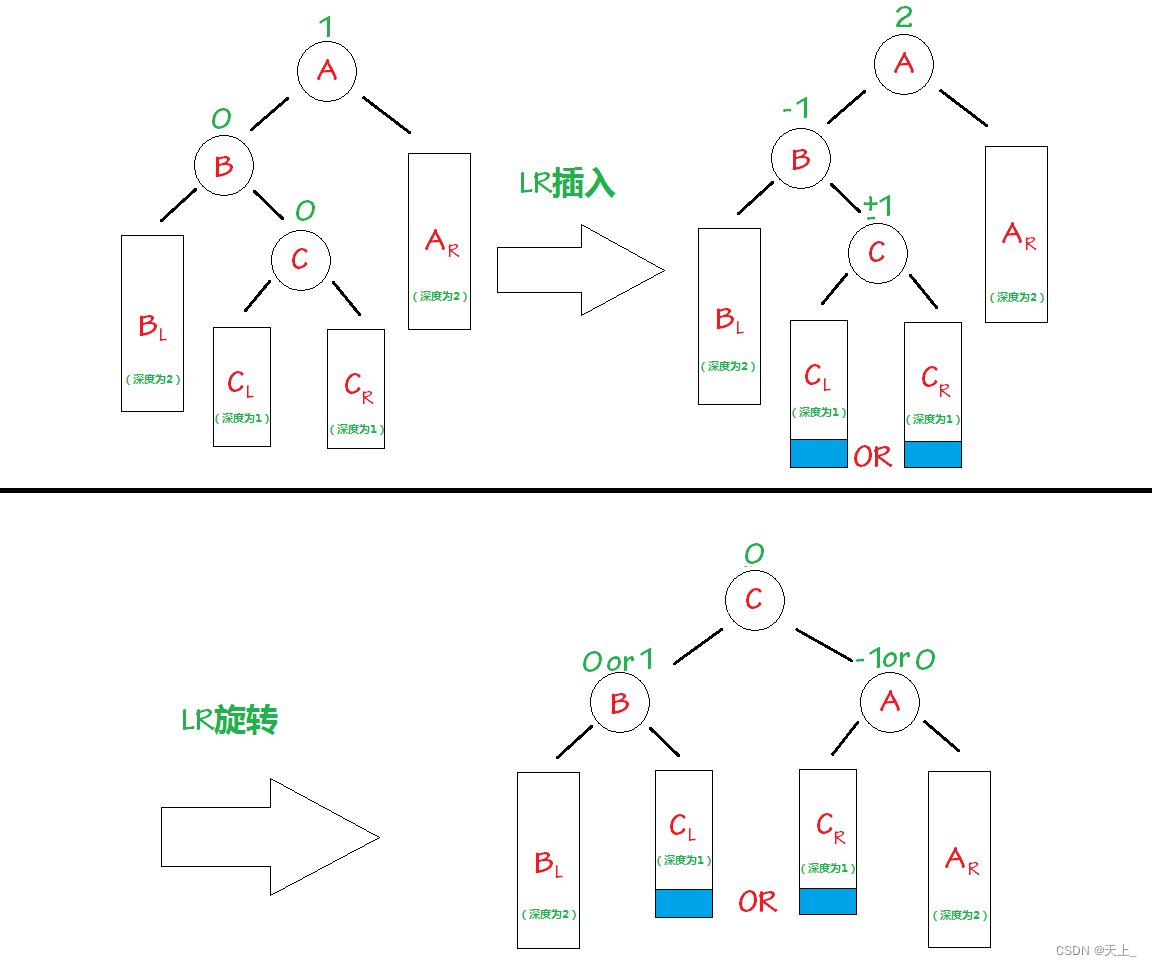
相关结点ABC旋转完之后，其余结点按原来的顺序接在B和A的左右子树中。

右左双旋 

 

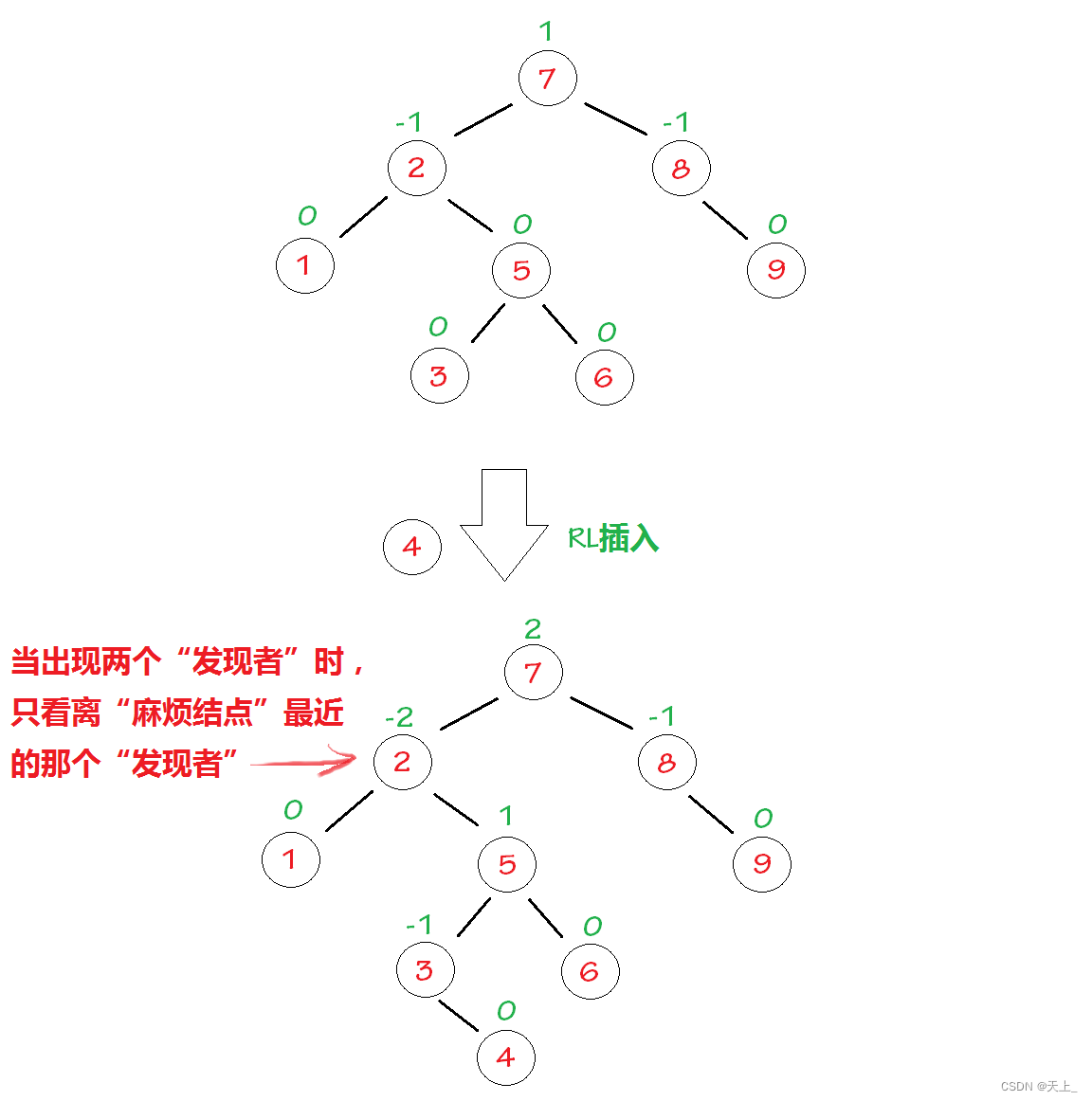
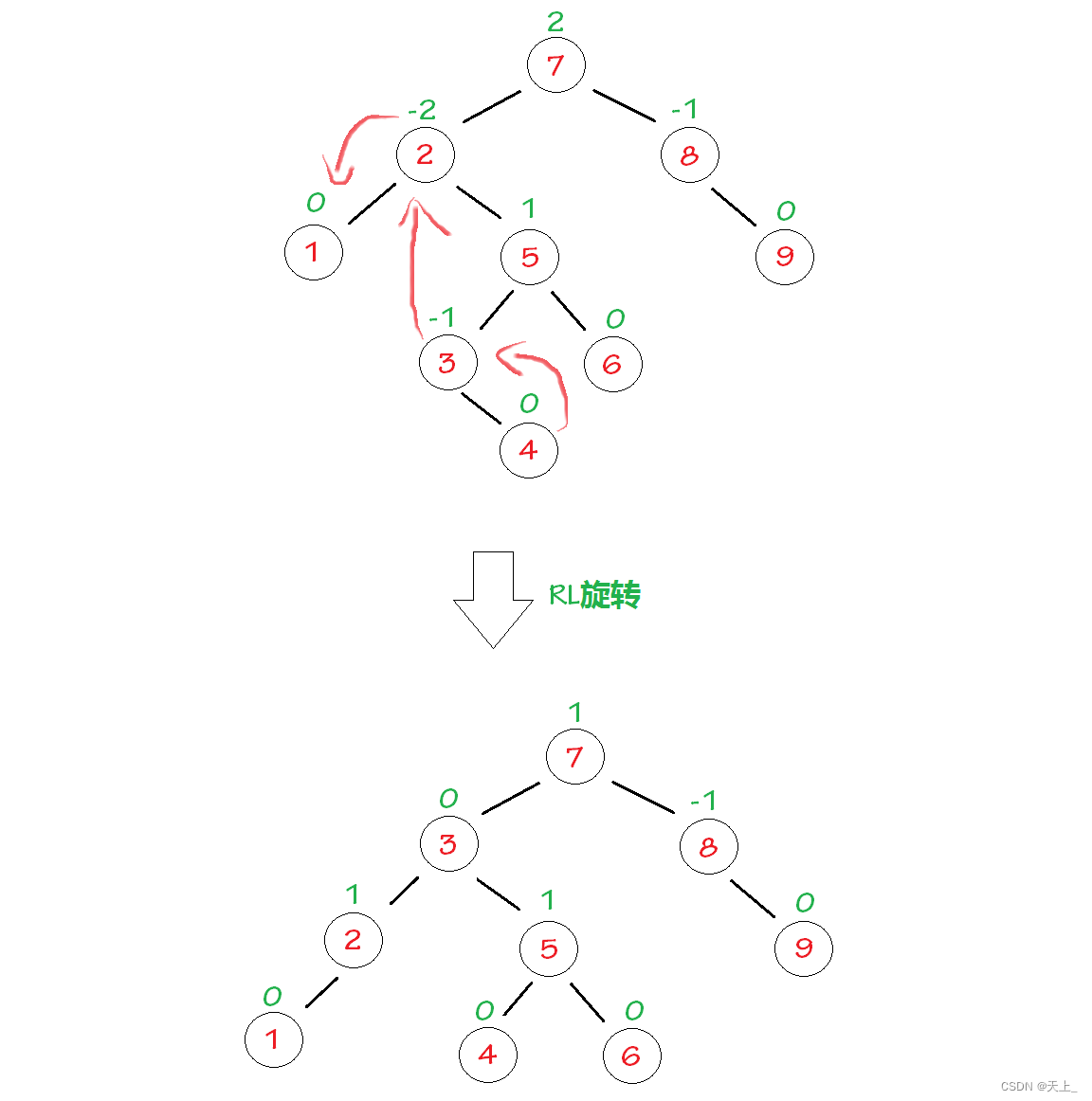
“发现者”是结点2,“麻烦结点”4在“发现者”右子树的左子树上，因而叫RL插入，需要进行RL旋转（右左双旋）。 

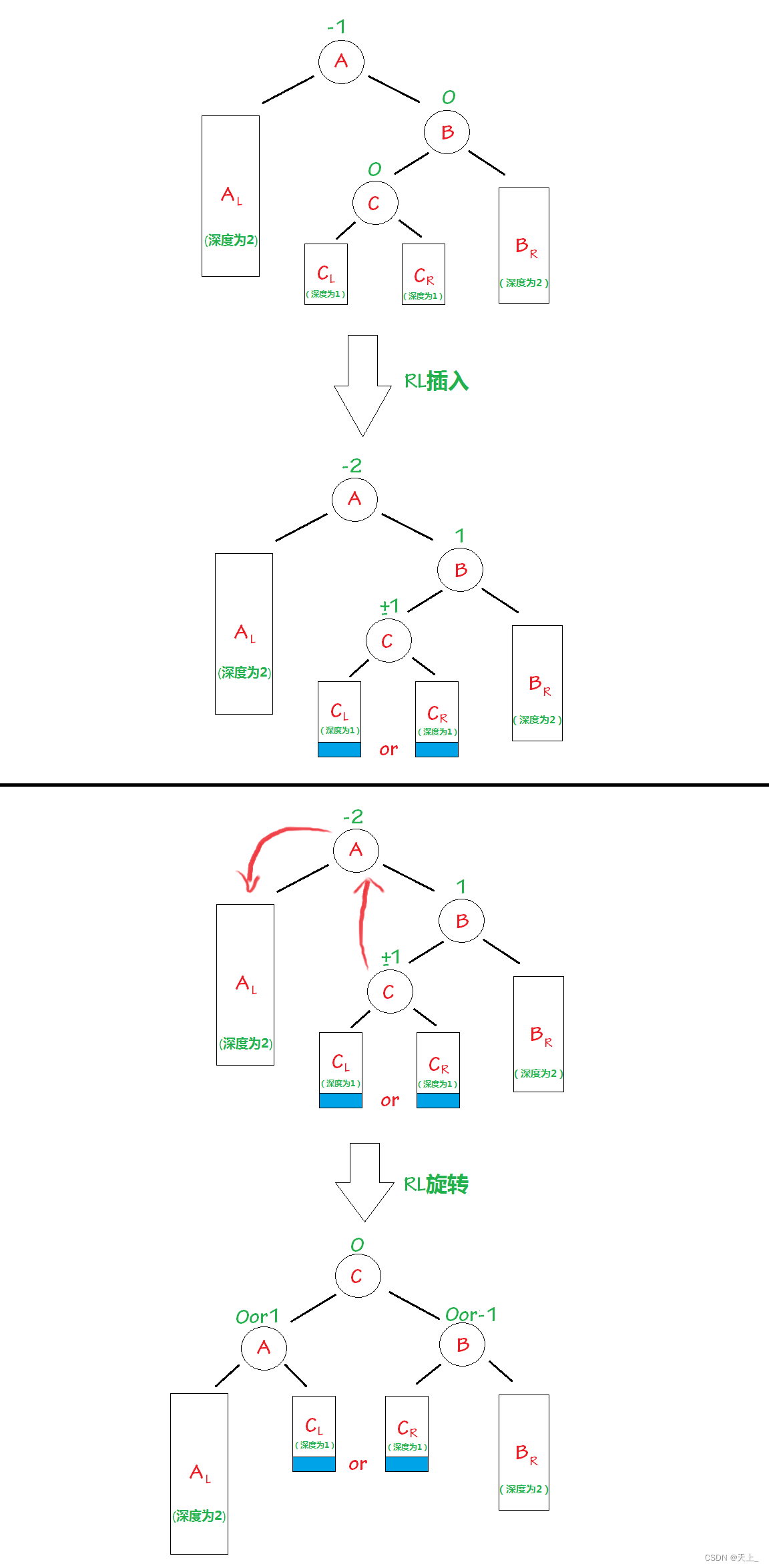
平衡因子的计算

有些时候，插入元素即便不需要调整结构，也可能需要重新计算一些平衡因子。

 

---

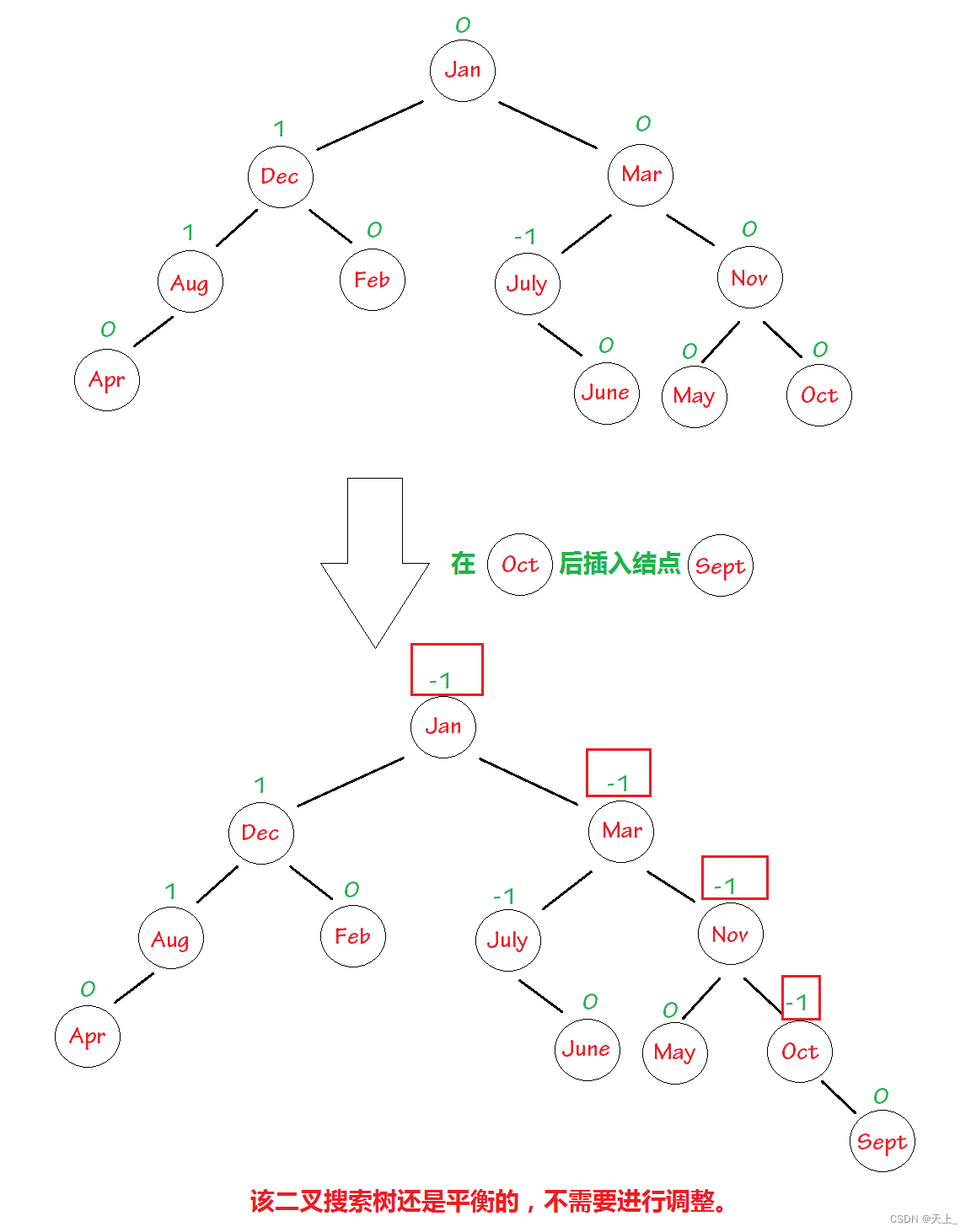
end

---

学习自：MOOC数据结构——陈越、何钦铭