1031. 两个非重叠子数组的最大和

类似问题转换

1. 考虑一个问题，如何求得数组中两个数的最大和。
   1. 可以固定一个数，然后向右遍历
   2. 如下，可以求得目标数组中两个数的最大和为 15

把思路实现为代码

1. 实现过程，如上图所示过程，右指针在移动过程中是跟随数组下标的
2. 左边部分的元素需要维护一个最大值，所以需要一个变量，保存左边元素的最大值
3. 需要求得最大和，所以需要一个变量保存最终结果
4. 最后一次遍历即可

def two_sum_max(nums: List[int]) -> int:
    ans, left = 0, 0
    for i in range(1, len(nums)):
        left = max(left, nums[i-1])
        ans = max(ans, left + nums[i])
    return ans

回到本题

1. 扩展数字到区间，求数组内两个不重叠的连续区间的和的最大值
2. 可以使用同样的思路，如下图

思路实现为代码

1. 首先最终返回一个最大值，需要一个变量保存最终结果
2. 遍历过程中可以计算右边部分的区间和
   1. 涉及到区间和需要联想到数组前缀和
   2. 所以需要实现求得数组的前缀和
3. 需要一个变量，在遍历过程中维护左边部分的最大值
   1. 最终结果=左边部分最大值+右边部分区间和
   2. 在遍历过程中不断比较得到最终结果
4. 需要注意在遍历过程中求前缀和的时候的下标计算控制

def max_two_gap_of_nums(nums: List[int], first_len: int, second_len: int) -> int:
    n = len(nums)
    for i in range(1, n):
        nums[i] = nums[i - 1] + nums[i]
    ans, left_max = 0, 0
    # 给 右边区间留足空间  遍历到  n - second_len
    # 区间 second_len 在后
    for i in range(first_len, n - second_len + 1):
        # 维护左边窗口的最大值的和
        # i 从 first_len 开始遍历，所要求的区间和位于  first_len 前面
        # 所以 有  nums[i - 1] - nums[i - first_len - 1]
        # 又因为 i - first_len - 1 有可能小于0，所以需要额外判断
        left_max = max(left_max, nums[i - 1] - (0 if (i - first_len - 1 < 0) else nums[i - first_len - 1]))
        # 左区间最大值 + 右边区间的最大值
        ans = max(ans, left_max + nums[i + second_len - 1] - nums[i - 1])
    # 区间 first_len 在后
    left_max = 0
    for i in range(second_len, n - first_len + 1):
        left_max = max(left_max, nums[i - 1] - (0 if (i - second_len - 1 < 0) else nums[i - second_len - 1]))
        ans = max(ans, left_max + nums[i + first_len - 1] - nums[i - 1])
    return ans

5. 优化
   1. 可以把 两个区间 依次排列在后面优化成一个方法

def better(nums: List[int], first_len: int, second_len: int) -> int:
    n = len(nums)
    for i in range(1, n):
        nums[i] = nums[i - 1] + nums[i]
    return max(two_gap_sum(nums, first_len, second_len), two_gap_sum(nums, second_len, first_len))


def two_gap_sum(nums: List[int], a: int, b: int) -> int:
    res, t = 0, 0
    for i in range(a, len(nums) - b + 1):
        t = max(t, nums[i-1] - (0 if (i - a - 1 < 0) else nums[i - a - 1]))
        res = max(res, t + nums[i + b - 1] - nums[i - 1])
    return res

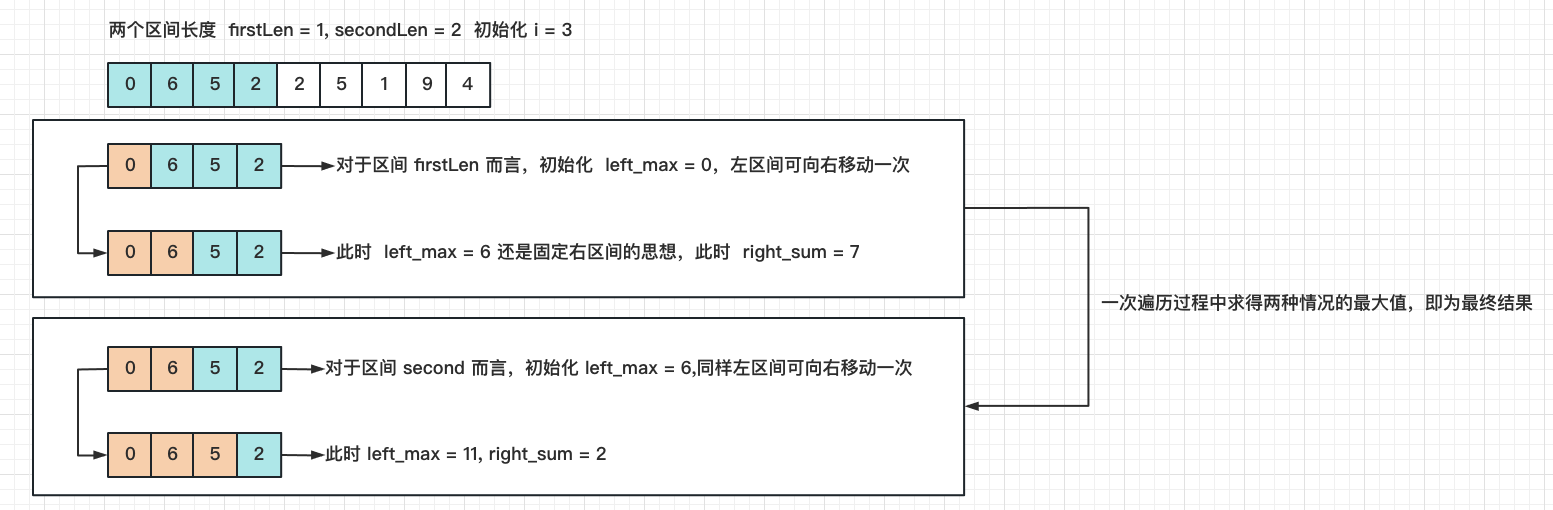
极其优雅的一次遍历

1. 上述思路都是分情况遍历数组两次
2. 实现思路的核心思想是固定一个窗口，然后求另一个窗口的最大值。然后再固定另一个窗口，进行两次遍历求得最终结果
3. 实际上该过程可以在一次遍历中搞定，如下图

def best_way(nums: List[int], a: int, b: int) -> int:
    n = len(nums)
    for i in range(1, n):
        nums[i] = nums[i] + nums[i - 1]
    res, left_max, right_max = nums[a + b - 1], nums[a - 1], nums[b - 1]
    for i in range(a+b, n):
        left_max = max(left_max, nums[i - b] - nums[i - a - b])
        right_max = max(right_max, nums[i - a] - nums[i - a - b])
        res = max(res, max(left_max + nums[i] - nums[i - b], right_max + nums[i] - nums[i - a]))
    return res

心得感悟

1. 通过学习 **lee **神的算法学习分享，要注重以下几点
   1. 切忌不要以做很多很多题为目标
   2. 培养对算法的兴趣
   3. 坚持写题解
   4. 不要怕浪费时间，万丈高楼平地起，坚持就好

参考

https://leetcode.cn/problems/maximum-sum-of-two-non-overlapping-subarrays/solution/python3javacgotypescript-yi-ti-yi-jie-qi-7nqt/
https://leetcode.cn/problems/maximum-sum-of-two-non-overlapping-subarrays/solution/ying-wen-ban-shang-pai-ming-di-yi-de-fei-chang-jin/
https://leetcode.cn/problems/maximum-sum-of-two-non-overlapping-subarrays/solution/qian-zhui-he-bian-li-onshi-jian-fu-za-du-ji-ke-qiu/