一、案例与数据

某研究者对企业员工进行调查，并且制定了一份问卷，研究者想要将问卷中的多个量表题进行浓缩以便后续分析，比如休假制度、资金制度、工资水平或者晋升制度等等，其中部分数据如下：

二、分析问题

其实想要将多个量表题进行信息浓缩，可以利用主成分分析进行研究，主成分分析是一种通过降维手段把多个变量化为少数几个主成分的统计方法，这些主成分能够反映原始变量的绝大部分信息，他们通常表述为原始变量的某种线性组合，以达到分析目的。

三、基本关系查看

并不是所有的数据都可以进行主成分分析，多数研究者希望通过主成分简化数据结构（降维），在这个基础上在进行分析，所以这就需要变量之间有线性相关关系，如果不存在线性相关关系，或者相关程度较低一般是不能进行主成分分析的。将数据进行相关分析，结果如下：

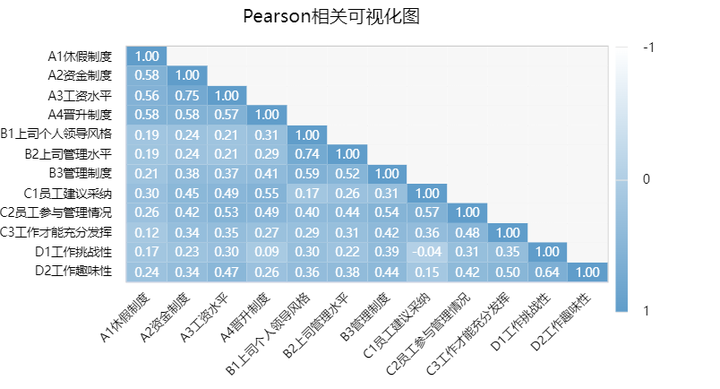
上数结果展示12个变量之间的相关关系，从整体来看，数据有相关关系的基础，可以进行主成分分析。

四、主成分结果解读

首先选择成分数，因为预设维度为4，所以成分选择“4”，如果说没有预设维度不知道应该划分为几个维度，则可以让系统自动选择，如下会说明。

1. KMO值与Bartlett检验

首先分析研究数据是否适合进行主成分分析，从上表可以看出：KMO为0.833，大于0.6，满足主成分分析的前提要求，以及数据通过Bartlett球形度检验(p<0.05)，说明研究数据适合进行主成分分析。

2、成分选择个数

当数据确定可以使用主成分分析后，下一步确定主成分成分选择个数，由于预设维度为4，所以成分选择“4”，如果没有预设维度，可以让系统自动选择，或者根据其它信息，一般有两个判断标准，特征值和碎石图。

1. 特征值
   一般会以特征值大于1为标准。
2. 碎石图

碎石图进行判断主观性较强，根据观察有明显下降趋势的拐点

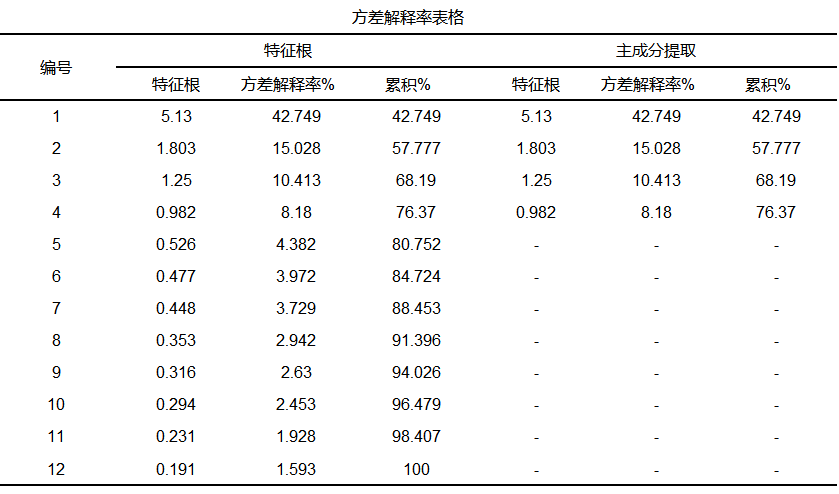
从上表可知：主成分分析将构建出4个主成分，特征根值均大于1，依次为5.13、1.803、1.25、0.982。此4个主成分的方差解释率分别是42.749%、15.028%、10.413%以及8.18%，累积方差解释率为76.37%。同时可以查看碎石图，如下：

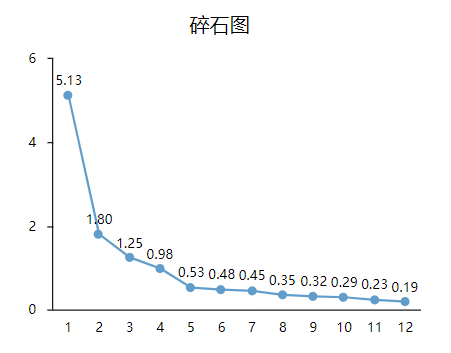
3、提取成分

将分析项构建成四个主成分，这些主成分各自与哪些指标有关系呢？总体上如何评价四个主成分的效果呢？载荷系数和共同度指标可以回答以上问题。

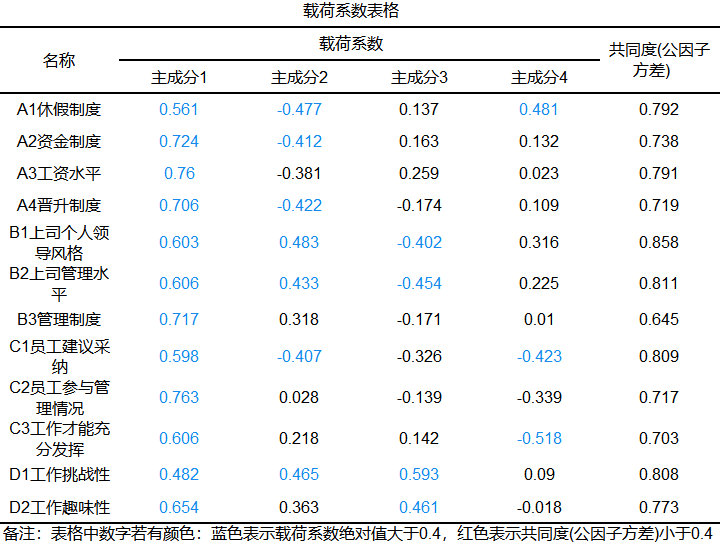
载荷系数反映了主成分与指标间的相关关系，共同度总体上反映所构建的主成分的解释能力。本案例的共同度在0.645~0.858之间，说明数据解释能力较好，但是发现主成分之间存在纠缠不清的情况，如果想要进行命名，这样的结果并不容易，所以可以利用“旋转”的策略，提高主成分命名的能力。结果如下：

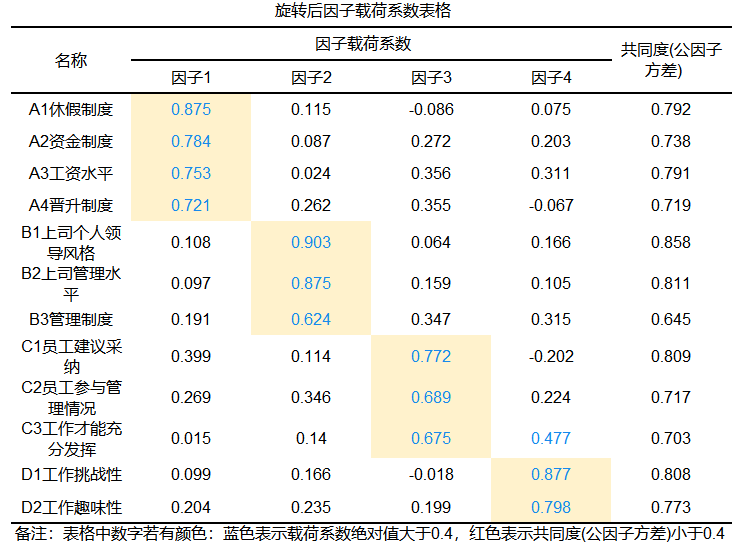
从结果中可以发现，第一主成分与休假制度、资金制度、工资水平、晋升制度有关；第二主成分与上司个人领导风格、上司管理水平以及管理制度有关；第三主成分与员工建议采纳、员工参与管理情况以及工作才能充分发挥有关；第四主成分与工作挑战性以及工作趣味性有关，如果想要进行命名，可以将主成分1命名为福利待遇、主成分2命名为管理及制度、主成分3命名为员工自主性、主成分4命名为工作性质。

五、总结

研究者想要将问卷中的多个量表题进行浓缩以便后续分析,使用主成分进行分析，首先进行查看数据的相关性，发现变量之间有一定的相关基础，进行主成分分析首先查看KMO值与Bartlett检验，发现检验通过，接着进行迷行成分选择个数和提取成分，最后得到四个主成分分别对应的变量。

案例数据：

SPSSAU - 案例数据​spssau.com/spssaudata.html?shareData=0B980C1A14041599C94F48B8A5A6E095