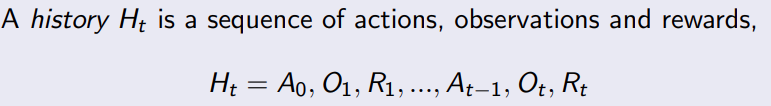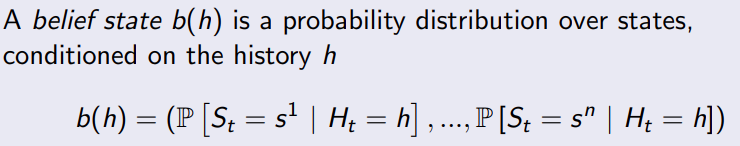1 Introduction
这个章节介绍关键的理论概念。
马尔科夫过程的作用:
1)马尔科夫过程描述强化学习环境的方法,环境是完全能观测的;
2)几乎所有的RL问题可以转换成MDP的形式;
2 Markov Processes
2.1 Markov 属性
属性1:未来和过去无关,只受当前的状态影响
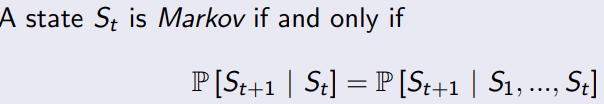
2.2 转移概率矩阵
从当前状态S转移到S’状态的概率,每行的概率之和为1.
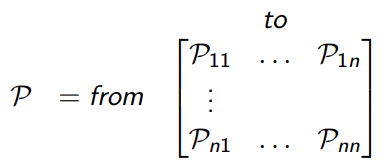
2.3 markov chains
马尔科夫过程是无记忆的随机过程,一串状态以及markov的属性。一个马尔科夫过程,只要有有限个状态,以及他们之间相互转换的概率,就可以构建。

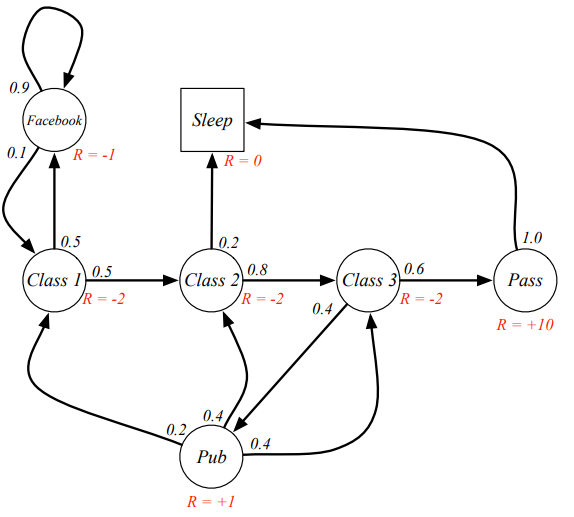
课程上给出了一个例子:
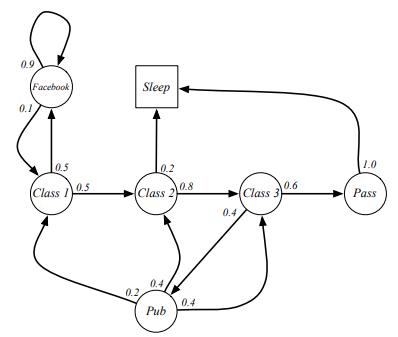
对应的转移概率矩阵

从class1 到 sleep有很多的链条

3 markov decision process
3.1 定义
马尔科夫奖励过程就是markov链和每个状态的reward
在马尔可夫决策过程(Markov Decision Process, MDP)中,奖励函数(reward function)是一个用于表示智能体在执行某个动作后所获得的即时奖励的函数。奖励函数通常用于指导智能体的行为,使其学会在面对不同的状态时做出对其最有利的决策。

3.2 return
从时刻t开始的总折扣奖励是Gt。这里的折扣奖励是指将未来的奖励按照一定的比例进行打折,以体现当前奖励的价值。通过调整
γ
\gamma
γ调整未来reward的权重。
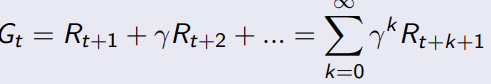
通过这个公式,可以算出来,从当前C1到最后SLEEP这个链的reward,比如可以用来选择走那条路径更优。

为什么要对后续的reward的添加权重
1.添加权重计算上比较简单;
2.避免循环马尔科夫链出现无穷大的情况
3.倾向于对眼前的利益
4.有时候也可能出现权重不衰减的情况;
3.3 value function
本质上还是用来评价当前这个状态好不好的,如何去评价,从当前状态到最终状态,可以积多少分
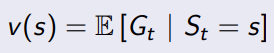
最简单的情况,
γ
=
0
\gamma=0
γ=0,完全不考虑未来
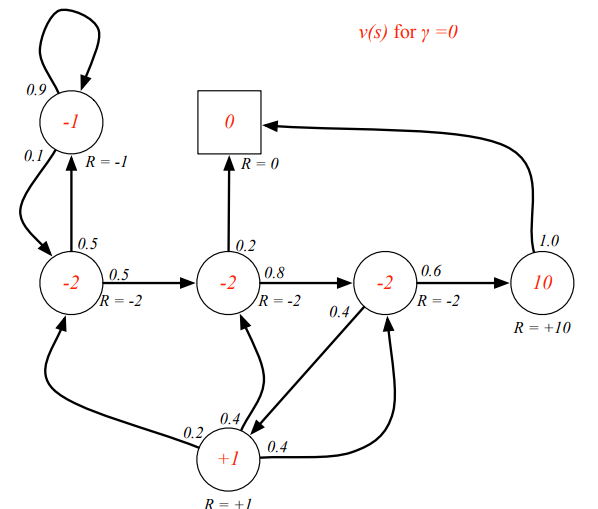
求一下S1 = C1,
γ
=
0.5
\gamma=0.5
γ=0.5的value值
问题:从S1=C1到最终的Sleep有很多条路径,那就有很多个结果,因为有状态概率矩阵,所以可以得到一个期望值?
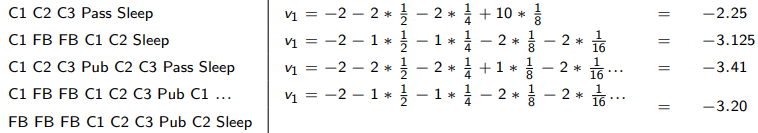
value function 必然选择最好的一条路径作为评价当前state的数值,这是一个典型的动态规划问题。
动态规划问题的思路就是将问题拆成更小的问题,当前
S
t
S_t
St的value function不知道,但是只要知道
S
t
+
1
S_{t+1}
St+1的状态,很容易得到当前时刻的value function。
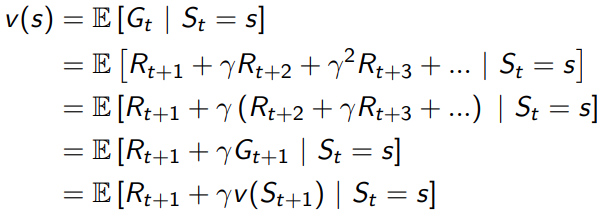
用图表示就是这个样子的
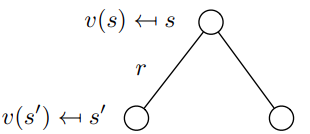
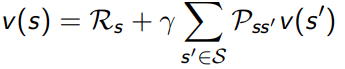
用动态规划的方法进行求解,且
γ
=
1
\gamma=1
γ=1,得到一下的markov 状态的value function.
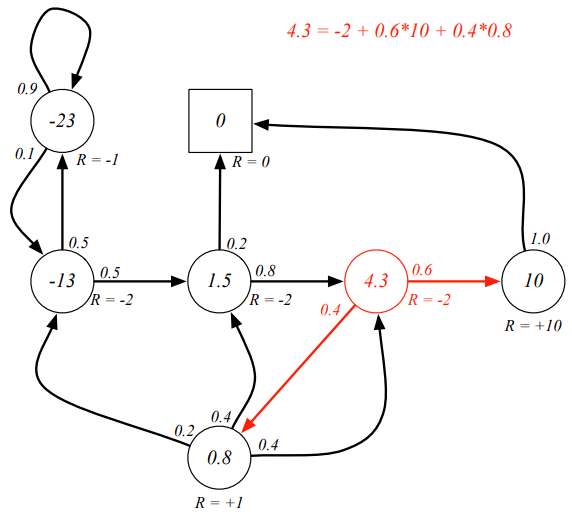
用矩阵的形式进行求解,
v
=
R
+
γ
∗
P
∗
v
v
=
(
I
−
γ
∗
P
)
−
1
R
\begin{aligned} v &= R + \gamma * P* v \\ v &= (I - \gamma *P)^{-1}R \end{aligned}
vv=R+γ∗P∗v=(I−γ∗P)−1R
验算一下上面的结果,因为$ (I - \gamma *P)$不可逆,比较悲剧,和上面这个结果差距很大,所以只能用其他方法来进行计算
,用value iteration的方法进行求解,因为我们这个问题维度比较小,只要最终状态收敛了就行。
function state_value = valueIterator(transition_matrix, reward_vector, discount_factor, tolerance)
n = size(transition_matrix, 1);
state_value = zeros(n, 1);
delta = inf;
while delta > tolerance
new_state_value = reward_vector + discount_factor * transition_matrix * state_value;
delta = max(abs(new_state_value - state_value));
state_value = new_state_value;
end
end
求解结果: -12.5432, 1.4568, 4.3210, 10.0000, 0.8025, -22.5432, 0
1)动态规划,对于我们这个问题,可以尝试用动态规划
2)monte-carlo evaluation
3) temporal difference learning
4 Markov decision processes
马尔科夫奖励过程上再加上决策;

从S到S’,是因为有action的推动。
问题:既然有action主动的去推动,还需要状态转移概率矩阵吗?
一种理解方式:处于当前状态S,有
P
s
s
′
a
P^a_{ss'}
Pss′a的概率去执行动作a;
4.1 policies
在马尔可夫决策过程(MDP)的环境中,策略是一个从状态到动作的映射,表示代理(Agent)在每个状态下选择采取哪个动作的规则。通常用π表示策略,即π(a|s)表示在状态s下采取动作a的概率

再来理解一下状态转移矩阵和policy矩阵的区别
状态转移矩阵(Transition Matrix):它表示在给定状态下执行某个动作后到达下一个状态的概率。状态转移矩阵的元素P(s’|s, a)表示在状态s下执行动作a,然后到达状态s’的概率。状态转移矩阵是MDP中一个固定的特性,与策略无关。它描述了在执行一个动作后,环境如何变化。
策略(Policy)矩阵:它表示在给定状态下选择执行某个动作的概率。策略矩阵的元素π(a|s)表示在状态s下选择执行动作a的概率。策略矩阵是MDP中的一个可调整的特性,可以根据需要选择不同的策略。它描述了在给定状态下,智能体如何选择执行动作。
考虑policy之后,从状态s到状态s’,要先经过一个状态概率输出动作a,然后再由 P s s ′ a P_{ss'}^a Pss′a的状态转移矩阵过去。
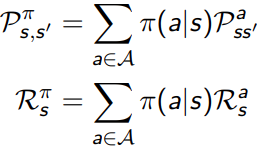
书中给的这两个关系,不太能理解
4.2 Value functions
4.2.1 state-value function
状态之间的转移如今不是单纯的确定概率了,而且可以通过策略进行调整了,在新策略之下,衡量当前S的状态评分。
状态价值函数 V(s):在状态 s 下遵循策略π的预期回报。即在状态 s 下,智能体采取策略π所能获得的长期回报的期望值。
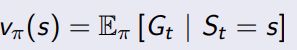
使用公式进行计算,
V
π
(
s
)
=
∑
a
∈
A
π
(
a
∣
s
)
[
R
(
s
,
a
)
+
γ
∑
s
′
∈
S
P
(
s
′
∣
s
,
a
)
V
π
(
s
′
)
]
V_{\pi}(s) = \sum_{a \in \mathcal{A}} \pi(a|s) \left[R(s, a) + \gamma \sum_{s' \in \mathcal{S}} P(s'|s, a) V_{\pi}(s')\right]
Vπ(s)=a∈A∑π(a∣s)[R(s,a)+γs′∈S∑P(s′∣s,a)Vπ(s′)]
从用下图去表示,
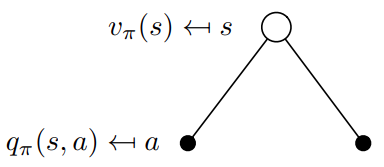
转换成矩阵形式,
v
π
(
s
)
v_{\pi}(s)
vπ(s)是一个
找一个简单的问题:
假设一个机器人处于一个4x4的网格世界,每个网格代表一个状态,共有16个状态(S1至S16)。机器人可以采取四个动作:上(U)、下(D)、左(L)和右(R)。假设机器人在状态S1(左上角),试图向右移动。然而,由于地面湿滑,机器人执行动作的不确定性使得实际移动方向可能发生偏移。
在这个例子中,当机器人试图从状态S1向右移动时,实际状态转移概率分布可能如下:
转移到状态S2(向右)的概率:0.8
转移到状态S5(向下)的概率:0.2
我们用一个4x4x4的张量来表示状态转移矩阵,第一维表示动作(上、下、左、右),第二维表示起始状态,第三维表示目标状态。这里我们仅提供一个概要的状态转移矩阵,仅包含部分非零元素
% 参数设置
num_states = 16;
num_actions = 4;
gamma = 0.9; % 折扣因子
theta = 1e-6; % 阈值,用于判断价值函数收敛
max_iter = 1000; % 最大迭代次数
% 状态转移矩阵 (4x16x16,对应于动作的顺序是:上、下、左、右)
P = zeros(num_actions, num_states, num_states);
% 定义状态转移矩阵的函数
% 省略了具体的状态转移矩阵实现,您可以根据之前的讨论来定义状态转移矩阵
% 奖励函数(16x4,行表示状态,列表示动作)
% 您可以根据实际问题自定义奖励函数
R = ...;
% 策略(16x4,行表示状态,列表示动作),均匀随机策略
policy = ones(num_states, num_actions) / num_actions;
% 初始化状态价值函数(1x16)
V = zeros(1, num_states);
% 迭代计算状态价值函数
for iter = 1:max_iter
V_old = V;
for s = 1:num_states
V_temp = 0;
for a = 1:num_actions
V_temp = V_temp + policy(s, a) * (R(s, a) + gamma * sum(P(a, s, :) .* V_old));
end
V(s) = V_temp;
end
% 判断价值函数是否收敛
if max(abs(V - V_old)) < theta
break;
end
end
% 输出状态价值函数
disp(V);
4.2.2 action value function
用于评估在给定策略下,一个状态下采取某个动作的长期价值。它表示从当前状态开始,首先执行某一特定动作,然后遵循给定策略,预期累计奖励的期望值。用Q(s, a)表示动作价值函数,其中s为状态,a为动作,Q(s, a)为在状态s下执行动作a的动作价值。
动作价值函数的意义在于,它可以帮助智能体在给定状态下选择最优的动作。通过比较不同动作的动作价值函数,智能体可以选择具有最高长期价值的动作,从而实现策略的优化。
为了选择最优的动作,智能体可以比较这些动作的动作价值函数Q(s, a),并选择具有最高价值的动作。例如,如果在当前位置,向右移动的动作价值函数Q(s, 右)最高,智能体将选择向右移动,以期望获得最大的累计奖励。
总之,状态价值函数V(s)用于评估在给定策略下,一个状态的长期价值;动作价值函数Q(s, a)用于评估在给定策略下,一个状态下采取某个动作的长期价值。动作价值函数对智能体具有重要意义,因为它可以帮助智能体在给定状态下选择最优的动作,从而实现策略的优化。
用action value function的定义就能看出,跟后续的状态的state value是相关的,接下来推导他们的关系。
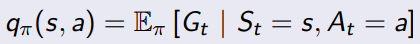
从公式来看,执行一连串的
Q
π
(
s
,
a
)
=
R
(
s
,
a
)
+
γ
∑
s
′
∈
S
P
(
s
′
∣
s
,
a
)
V
π
(
s
′
)
Q^{\pi}(s, a) = R(s, a) + \gamma \sum_{s' \in S} P(s'|s, a) V^{\pi}(s')
Qπ(s,a)=R(s,a)+γs′∈S∑P(s′∣s,a)Vπ(s′)
这个公式很容易理解,
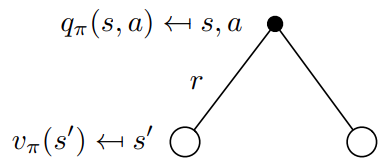
4.2.3 用bellman function 总结上面的关系
V π ( s ) = ∑ a ∈ A π ( a ∣ s ) [ R ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V π ( s ′ ) ] R π ( s ) = ∑ a ∈ A π ( a ∣ s ) R ( s , a ) P π ( s ′ ∣ s ) = ∑ a ∈ A ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V π ( s ) = R π ( s ) + γ P π ( s ′ ∣ s ) V π ( s ) \begin{aligned} V_{\pi}(s) &= \sum_{a \in \mathcal{A}} \pi(a|s) \left[R(s, a) + \gamma \sum_{s' \in \mathcal{S}} P(s'|s, a) V_{\pi}(s')\right] \\ R^{\pi} (s)& = \sum_{a \in \mathcal{A}} \pi(a|s) R(s, a) \\ P^{\pi}(s'|s) & = \sum_{a \in \mathcal{A}} \sum_{s' \in \mathcal{S}} P(s'|s, a) \\ V_{\pi}(s) & = R^{\pi}(s)+\gamma P^{\pi}(s'|s) V_{\pi}(s) \end{aligned} Vπ(s)Rπ(s)Pπ(s′∣s)Vπ(s)=a∈A∑π(a∣s)[R(s,a)+γs′∈S∑P(s′∣s,a)Vπ(s′)]=a∈A∑π(a∣s)R(s,a)=a∈A∑s′∈S∑P(s′∣s,a)=Rπ(s)+γPπ(s′∣s)Vπ(s)
看一下带policy的reward的应该如何定义,R(s,a)表示处于状态s情况下,采用动作a的奖励,
R
π
R^{\pi}
Rπ表示在给定策略π下,智能体在状态s采取不同动作a的期望奖励。
4.3 optimal value functions
4.3.1 optimal state value function
找一个最好的policy去最大化状态value function
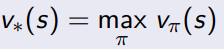
找一个最好的policy去最大化action value function
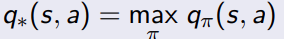
定义什么是最优的policy
所有的state, 取得了最大的value function
所有的action,取得了最大的action value 数值
4.3.2 如何寻找optimal policy
简单理解就是要最大化action value的期望。
要确定全局的最优策略,我们需要关注的是状态-动作价值函数(state-action value function),也被称为Q-function。Q-function 衡量了在特定策略下,从某一状态(state)采取某一动作(action)开始所能获得的期望累积奖励。我们可以使用贝尔曼最优方程(Bellman optimality equation)来寻找最优策略。
再来回顾一下action value function的定义,
Q
π
(
s
,
a
)
=
R
(
s
,
a
)
+
γ
∑
s
′
∈
S
P
(
s
′
∣
s
,
a
)
V
π
(
s
′
)
V
π
(
s
)
=
∑
a
∈
A
π
(
a
∣
s
)
[
R
(
s
,
a
)
+
γ
∑
s
′
∈
S
P
(
s
′
∣
s
,
a
)
V
π
(
s
′
)
]
Q
∗
(
s
,
a
)
=
R
(
s
,
a
)
+
γ
∑
s
′
∈
S
P
(
s
′
∣
s
,
a
)
V
∗
(
s
′
)
V
∗
(
s
)
=
max
a
(
R
(
s
,
a
)
+
γ
∑
s
′
P
(
s
′
∣
s
,
a
)
V
∗
(
s
′
)
)
\begin{aligned} Q^{\pi}(s, a) &= R(s, a) + \gamma \sum_{s' \in S} P(s'|s, a) V^{\pi}(s') \\ V_{\pi}(s) &= \sum_{a \in \mathcal{A}} \pi(a|s) \left[R(s, a) + \gamma \sum_{s' \in \mathcal{S}} P(s'|s, a) V_{\pi}(s')\right]\\ Q^{*}(s, a) &= R(s, a) + \gamma \sum_{s' \in S} P(s'|s, a) V^{*}(s') \\ V^*(s) & = \max_a \left( R(s, a) + \gamma \sum_{s'} P(s'|s, a) V^*(s') \right) \\ \end{aligned}
Qπ(s,a)Vπ(s)Q∗(s,a)V∗(s)=R(s,a)+γs′∈S∑P(s′∣s,a)Vπ(s′)=a∈A∑π(a∣s)[R(s,a)+γs′∈S∑P(s′∣s,a)Vπ(s′)]=R(s,a)+γs′∈S∑P(s′∣s,a)V∗(s′)=amax(R(s,a)+γs′∑P(s′∣s,a)V∗(s′))
重要的公式1,optimal value function 和optimal action value function的关系
V
∗
(
s
)
=
max
a
Q
∗
(
s
,
a
)
V^*(s) = \max_a Q^*(s, a)
V∗(s)=amaxQ∗(s,a)
它表示在状态
s
s
s下,最优状态价值函数
V
∗
(
s
)
V^*(s)
V∗(s)等于所有可能动作的最优状态-动作价值函数
Q
∗
(
s
,
a
)
Q^*(s, a)
Q∗(s,a)的最大值。换句话说,如果我们遵循最优策略,在状态
s
s
s下,我们会选择那个能让我们获得最大期望累积奖励的动作。
从理解的角度, state的value和最优的action的结果相同,
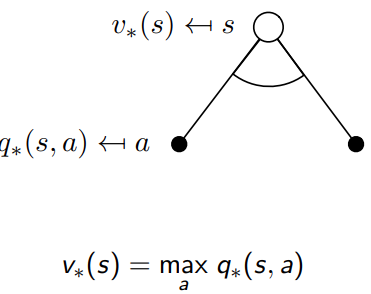
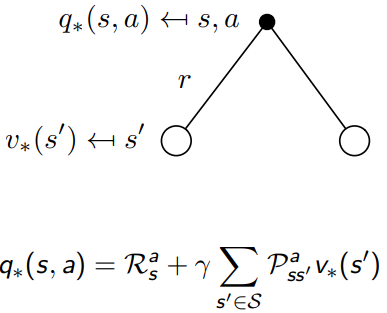
重要的公式2,optimal value function 和optimal action value function的关系
Q
∗
(
s
,
a
)
=
R
(
s
,
a
)
+
γ
∑
s
′
∈
S
P
(
s
′
∣
s
,
a
)
V
∗
(
s
′
)
V
∗
(
s
)
=
max
a
(
R
(
s
,
a
)
+
γ
∑
s
′
P
(
s
′
∣
s
,
a
)
V
∗
(
s
′
)
)
\begin{aligned} Q^{*}(s, a) &= R(s, a) + \gamma \sum_{s' \in S} P(s'|s, a) V^{*}(s') \\ V^*(s) & = \max_a \left( R(s, a) + \gamma \sum_{s'} P(s'|s, a) V^*(s') \right) \\ \end{aligned}
Q∗(s,a)V∗(s)=R(s,a)+γs′∈S∑P(s′∣s,a)V∗(s′)=amax(R(s,a)+γs′∑P(s′∣s,a)V∗(s′))
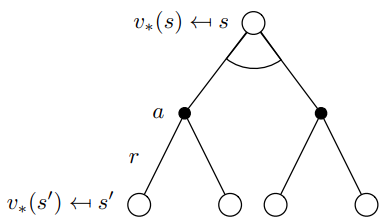
Q
∗
(
s
,
a
)
=
R
(
s
,
a
)
+
γ
∑
s
′
∈
S
P
(
s
′
∣
s
,
a
)
V
∗
(
s
′
)
Q
∗
(
s
,
a
)
=
R
(
s
,
a
)
+
γ
∑
s
′
∈
S
P
(
s
′
∣
s
,
a
)
max
a
′
q
∗
(
s
′
,
a
′
)
\begin{aligned} Q^{*}(s, a) &= R(s, a) + \gamma \sum_{s' \in S} P(s'|s, a) V^{*}(s') \\ Q^{*}(s, a) &= R(s, a) + \gamma \sum_{s' \in S} P(s'|s, a) \max_{a'} q^*(s',a') \end{aligned}
Q∗(s,a)Q∗(s,a)=R(s,a)+γs′∈S∑P(s′∣s,a)V∗(s′)=R(s,a)+γs′∈S∑P(s′∣s,a)a′maxq∗(s′,a′)
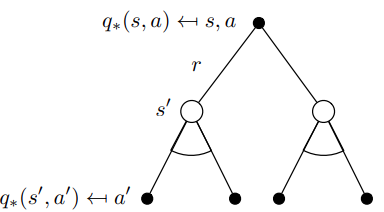
求解的办法
1)value iteration
2) Policy iteration
3) Q-learning
4) Sarsa
5 Extensions to MDPs
5.1 infinite and continuous mdps
- Countably infinite state and/or action spaces
- Straightforward
- Continuous state and/or action spaces
- closed form for linear quadratic model
- continuous time
- 需要微分动态方程
- HJB 方程
- limiting case of Bellman equation as time-step
5.2 Partially observable MDPs

5.2.1 belief states