剑指 Offer 42. 连续子数组的最大和 - 力扣(Leetcode)
输入一个整型数组,数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。
实例:
输入: nums = [-2,1,-3,4,-1,2,1,-5,4] 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
根据时间复杂度的要求:所以要求我们只能遍历组一遍,所以我们的操作必须精细。
这里数据我们在使用三个变量来完成题目要求;
int maxSubArray(int* nums, int numsSize){
}画图建思路:

prev保存的是当前移动连续元素的最大值
max保存的是目前数据最大的连续数据。
i 下标在数组中移动
初始化数据不可设置未0,为了防止数组中全部都是负数,使用我们初始化prev与max都为数组第一个元素。
因为题目给出数据至少有一个,所以 i 从第二个元素开始防止数组只有一个数据时出错。
当i>=numsSize时循环结束放回max数据。
开始操作
当 i 移动到下标 1 时,比较prev+nums[1]与nums[1]的大小如果前者大就原prev+nums[1]相加赋予新prev。如果后者大放弃原prev,将nums[i]单独赋予新prev,然后将新prev与原max比较,较大值赋予新max。
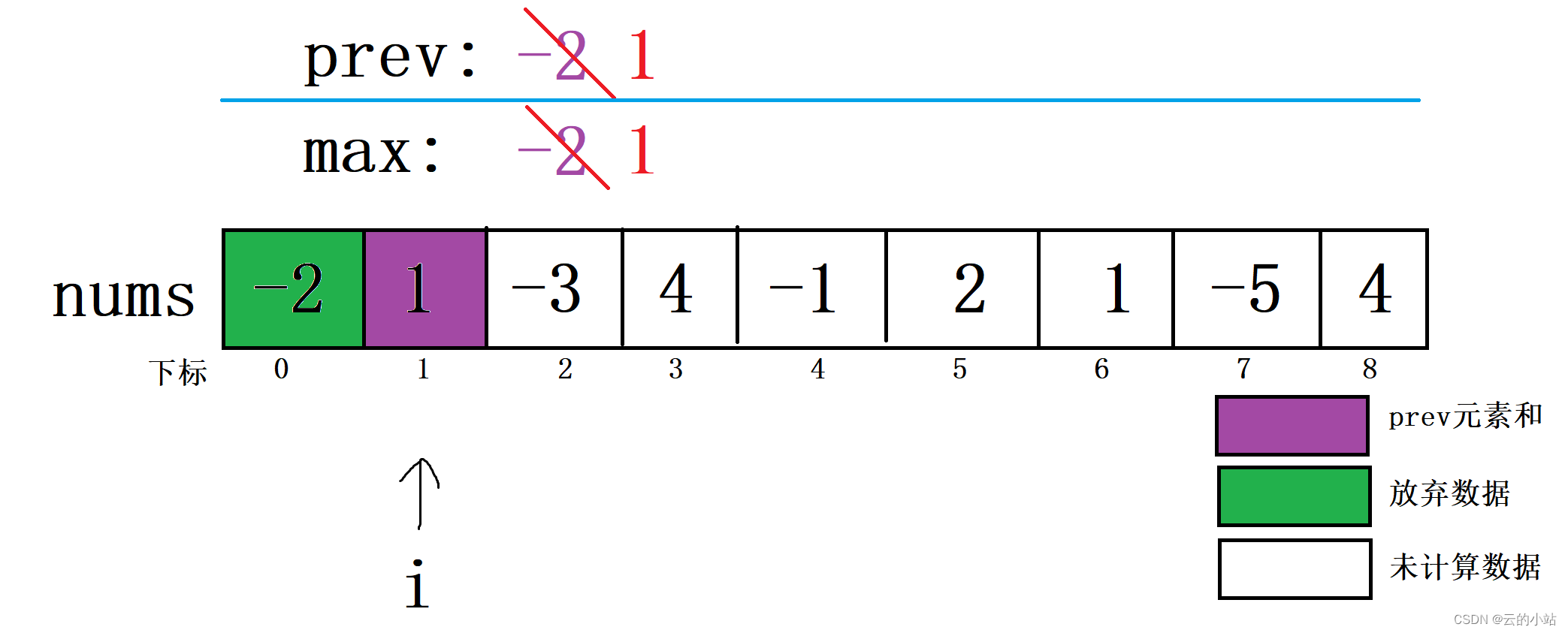
这里的prev加上下标1元素大于下标1元素,新prev=下标2。当前新prev大于原max,新max=新prev
i继续移动,i=2,比较prev+nums[2]与nums[2]的大小,将较大数据赋予新prev。然后将新prev与原max比较,较大值赋予新max。
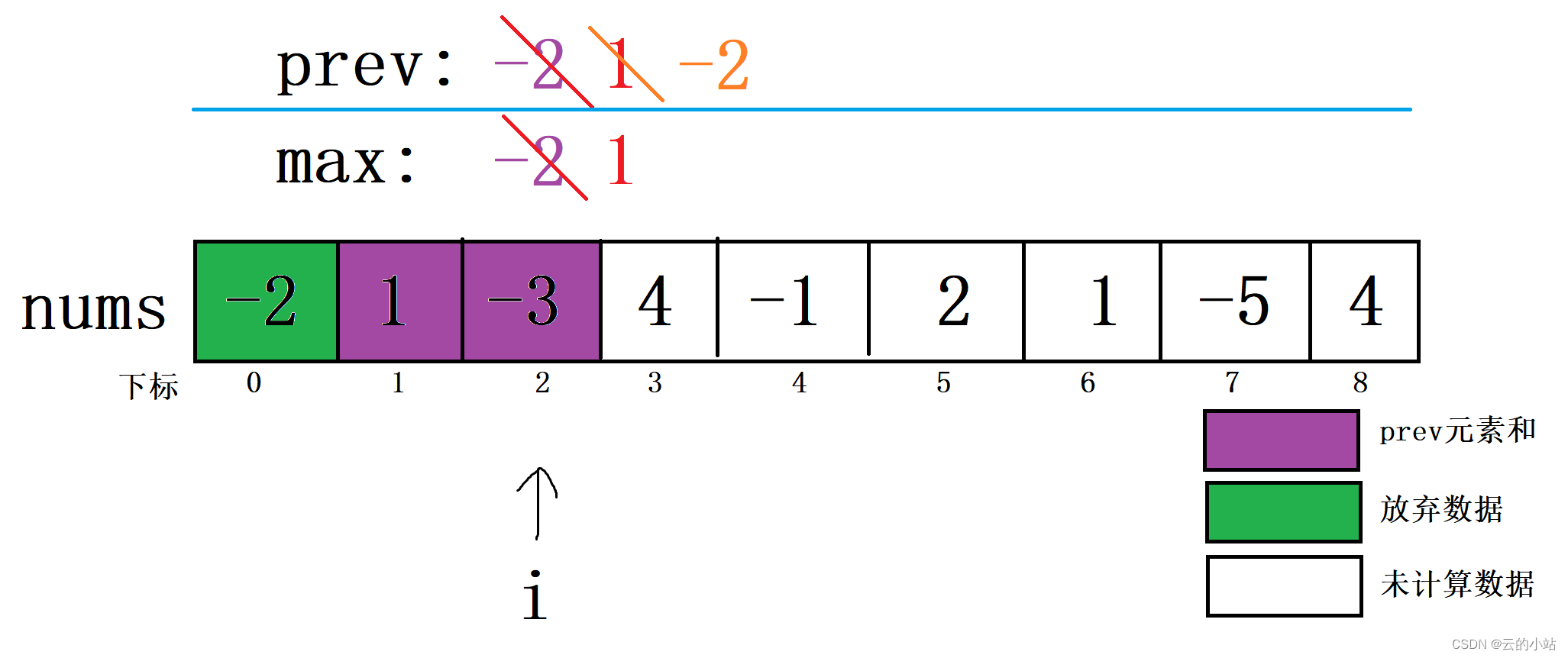
这里的prev加上下标2元素大于下标2元素,新prev=原prev+下标2。当前新prev小于max,max不改变。
i继续移动,i=3,比较prev+nums[3]与nums[3]的大小,将较大数据赋予新prev。然后将新prev与原max比较,较大值赋予新max。

这里的prev加上下标3元素小于下标3元素,放弃之前所有累加数据,只保存当前下标3数据。当前新prev大于原max,新max=新prev
i继续移动,i=4,比较prev+nums[4]与nums[4]的大小,将较大者赋予新prev。然后将新prev与原max比较,较大值赋予新max。
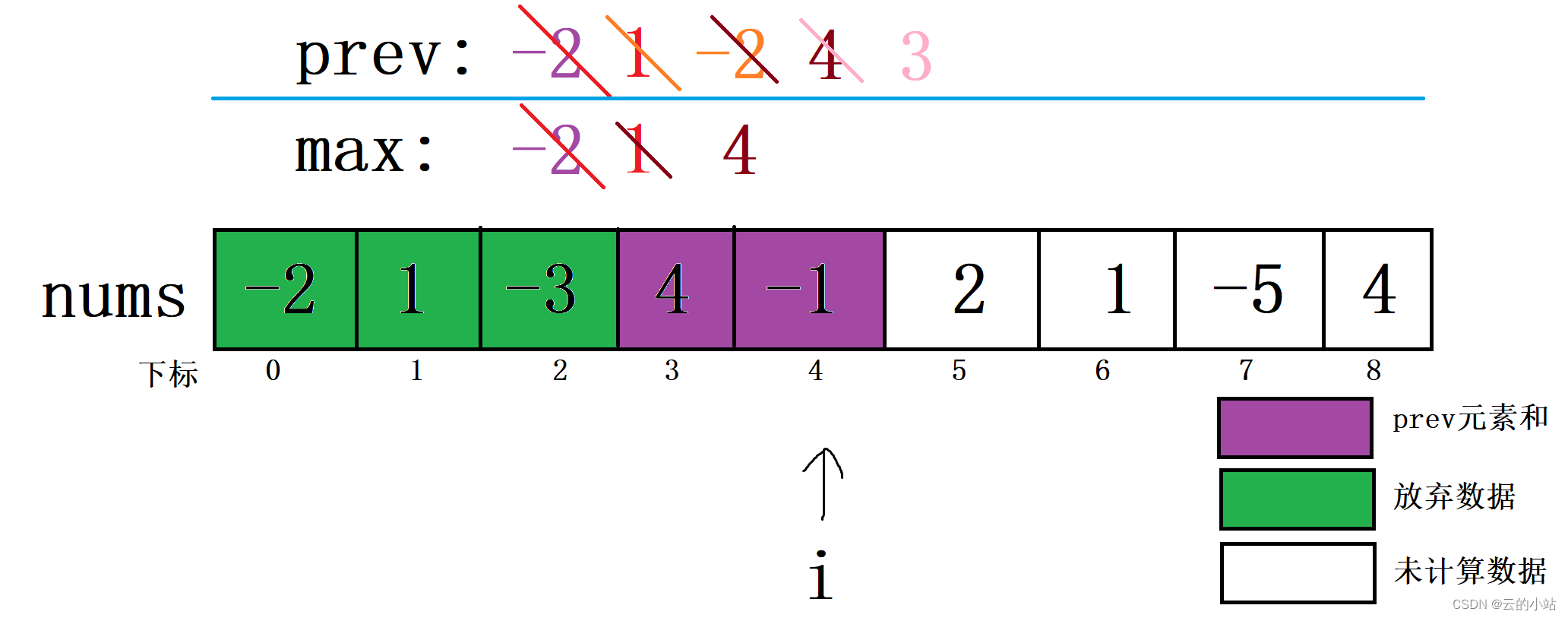
这里的prev加上下标4元素大于下标4元素,新prev=原prev+下标4。当前新prev小于max,max不改变。
i继续移动,i=5,比较prev+nums[5]与nums[5]的大小,将较大数据赋予新prev。然后将新prev与原max比较,较大值赋予新max。
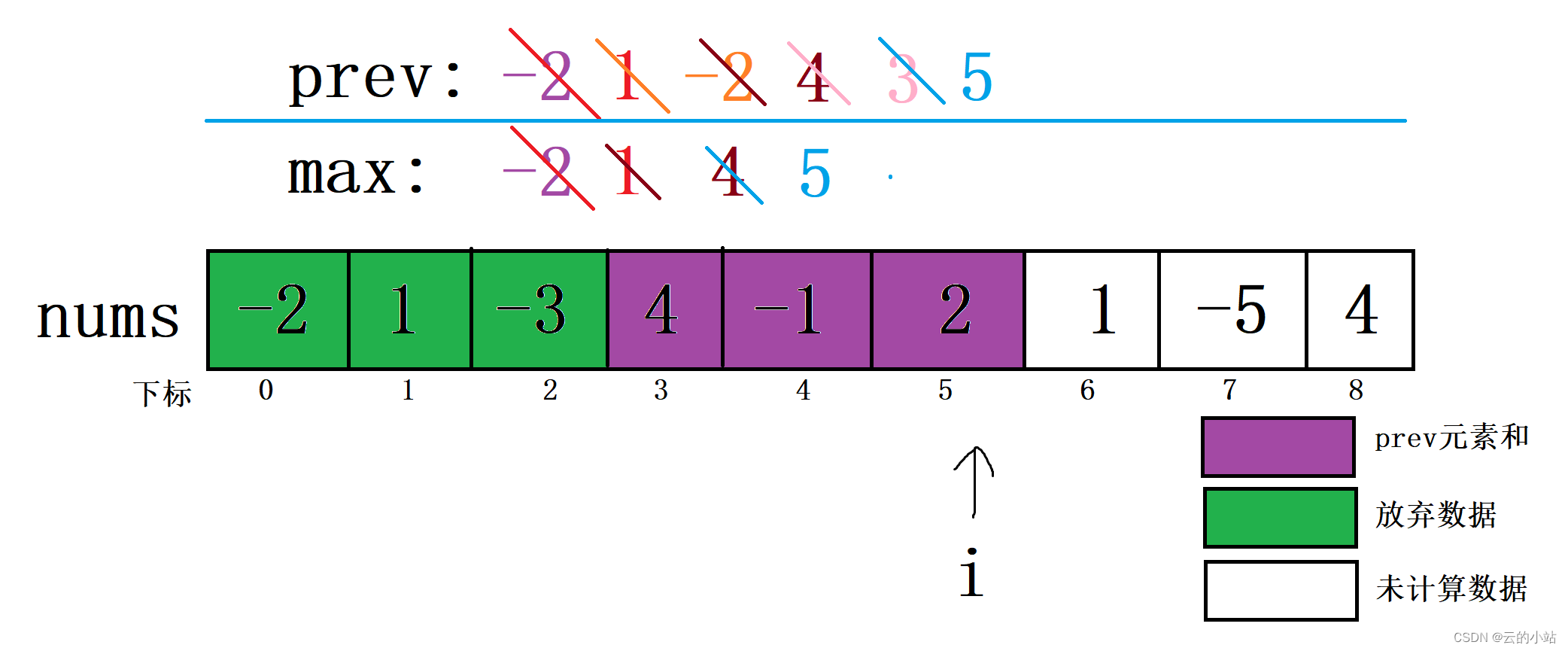
这里的prev加上下标5元素大于下标5元素,新prev=原prev+下标5。当前新prev大于原max,新max=新prev
i继续移动,i=6,比较prev+nums[6]与nums[6]的大小,将较大数据赋予新prev。然后将新prev与原max比较,较大值赋予新max。
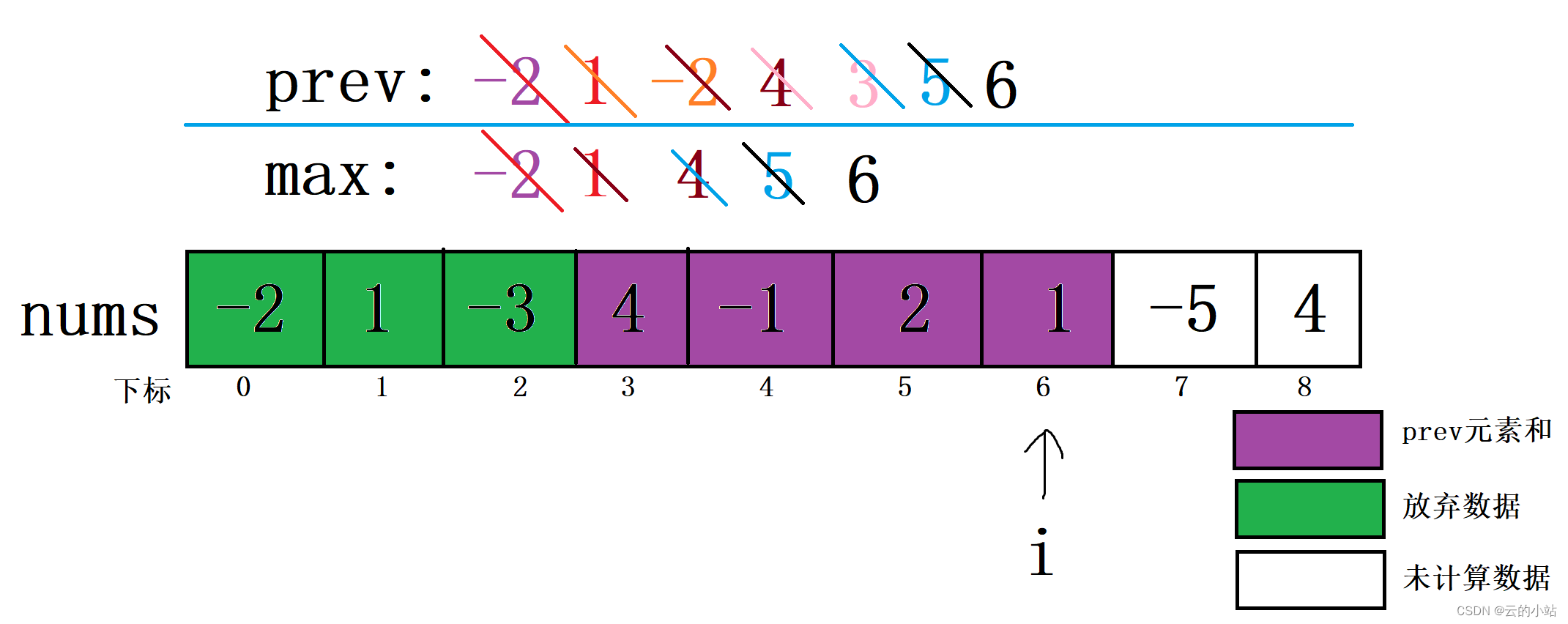
这里的prev加上下标6元素大于下标6元素,新prev=原prev+下标6。当前新prev大于原max,新max=新prev
i继续移动,i=7,比较prev+nums[7]与nums[7]的大小,将较大数据赋予新prev。然后将新prev与原max比较,较大值赋予新max。
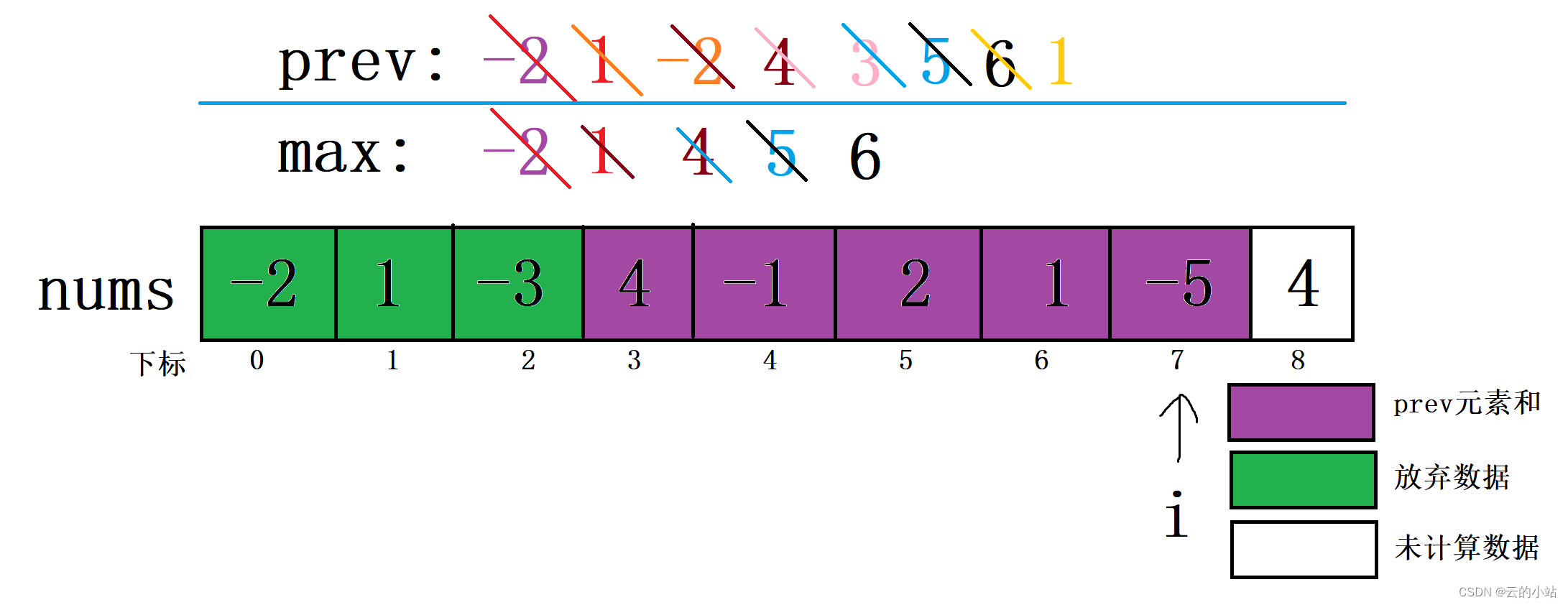
这里的prev加上下标7元素大于下标7元素,新prev=原prev+下标7。当前新prev小于max,max不改变。
i继续移动,i=8,比较prev+nums[8]与nums[8]的大小,将较大数据赋予新prev。然后将新prev与原max比较,较大值赋予新max。
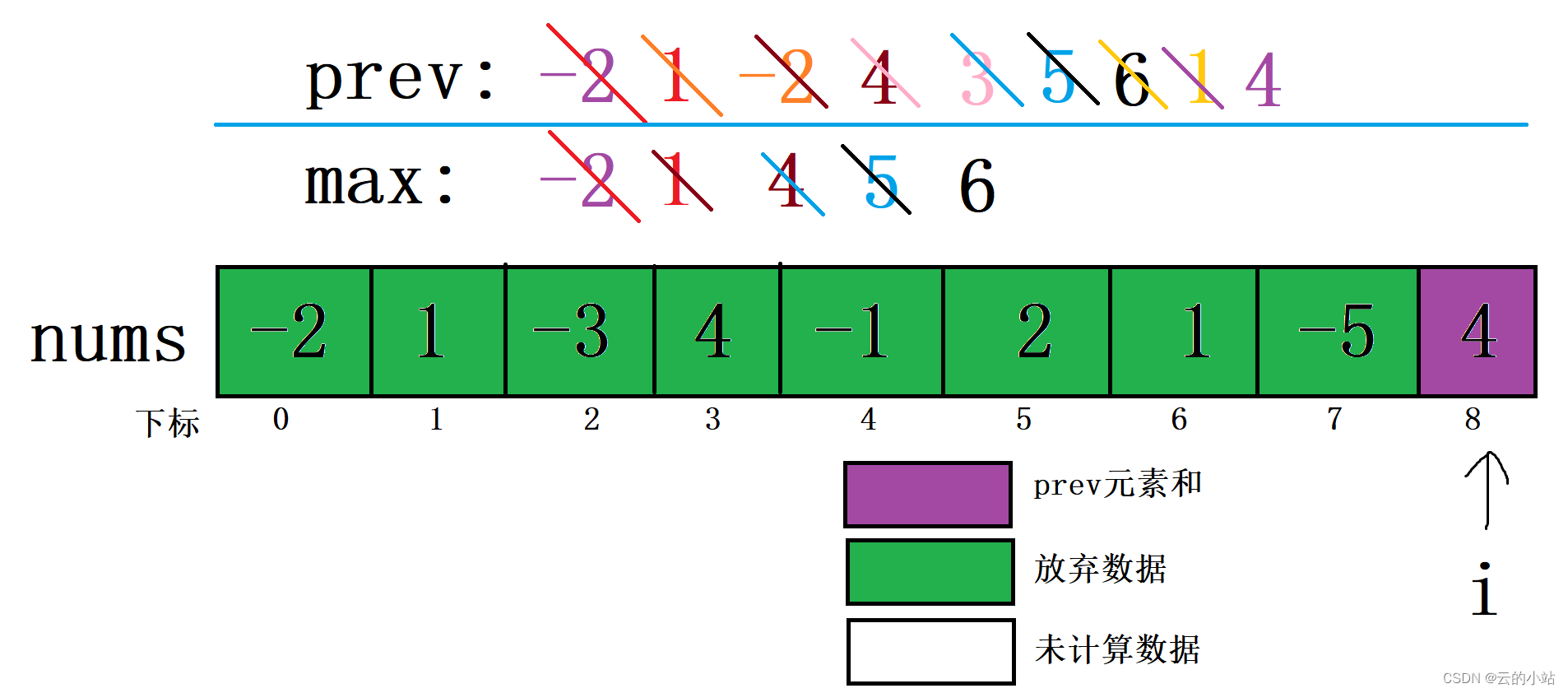
这里的prev加上下标8元素大于下标8元素,新prev=下标8。当前新prev小于max,max不改变。
i继续移动,i超出数组访问,循环结束,时间复杂度为O(N)复合要求。返回数据max,得出答案,该数组的连续子数组的最大和为:6。
代码实现
//使用long long 长整型防止数据过大!!!
long long fun_max(long long e1,long long e2)
{
return e1>e2?e1:e2;
}
int maxSubArray(int* nums, int numsSize){
long long prev=nums[0];
long long max=nums[0];
for(int i=1;i<numsSize;i++)
{
prev=fun_max(prev+nums[i],nums[i]);
max=fun_max(prev,max);
}
return max;
}
谢谢观看!!!!