DOA波达方向估计

DOA（Direction Of Arrival）波达方向是指通过阵列信号处理来估计来波的方向，这里的信源可能是多个，角度也有多个。DOA技术主要有ARMA谱分析、最大似然法、熵谱分析法和特征分解法，特征分解法主要有MUSIC算法、ESPRIT算法WSF算法等。其中MUSIC是一种经典的DOA估计算法。

MUSIC算法概述

MUSIC(multiple signal classification algorithm)算法是一种基于矩阵特征空间分解的方法。从几何角度讲，信号处理的观测空间可以分解为信号子空间和噪声子空间，显然这两个空间是正交的。信号子空间由阵列接收到的数据协方差矩阵中与信号对应的特征向量组成，噪声子空间则由协方差矩阵中所有最小特征值（噪声方差）对应的特征向量组成。

MUSIC算法原理

MUSIC算法是空间谱估计测向理论的重要基石。算法原理 如下：
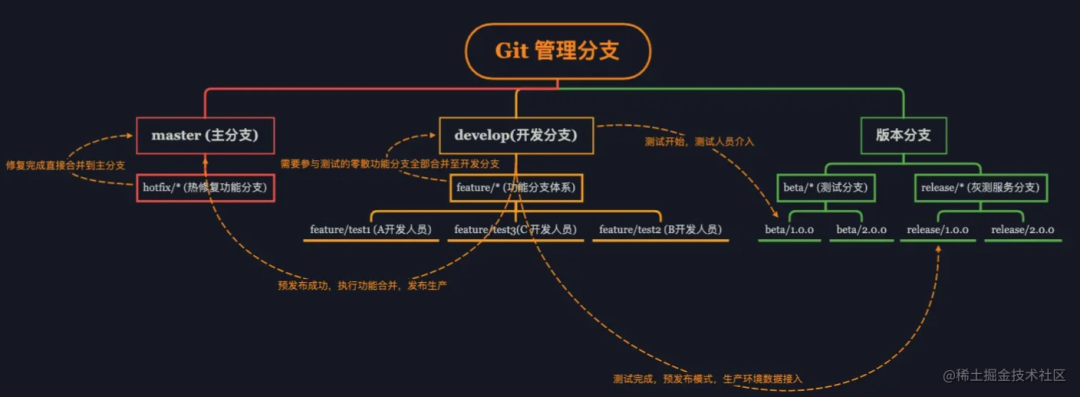
（1） 不管测向天线阵列形状如何，也不管入射来波入射角的维数如何，如图1所示，假定阵列由$N$个阵元组成，并且符合窄带、远场模型。

图1. 均匀线性阵模型

则阵列输出模型的矩阵形式都可以表示为：$Y(t)=AX(t)+N(t)$
其中，$Y$是观测到的阵列输出数据复向量；$X$是未知的空间信号复向量；$N(t)$是阵列输出向量中的加性噪声；$A$是阵列的方向矩阵，又称之为阵列流形矩阵；当我们以最左侧的阵元为参考位，此处，$A$矩阵表达式表示为：
$$A=[\alpha ({\theta }_1),\alpha ({\theta }_2),\cdots ,\alpha ({\theta }_M)]=\begin{array}{c}\left[\begin{array}{cccc}1& 1& \cdots & 1\\ e^{-j{\varphi }_1}& e^{-j{\varphi }_2}& \cdots & e^{-j{\varphi }_D}\\ e^{j-2{\varphi }_1}& e^{-j2{\varphi }_2}& \cdots & e^{-j2{\varphi }_D}\\ ⋮& ⋮& \ddots & ⋮\\ e^{-j(N-1){\varphi }_1}& e^{-j(N-1){\varphi }_2}& \cdots & e^{-j(N-1){\varphi }_D}\end{array}\right]\end{array}$$
其中，${\varphi }_k=2\pi sin{\theta }_k/\lambda$，且${\theta }_k,1\le k\le D$为第$k$个信源的角度，共有$D$个角度。${\varphi }_k$在这里是指波程差引起的相移，如下图所示相邻阵元之间的波程差为$dsin\theta$，将此转换为相位，单位为弧度，则为$2\pi sin{\theta }_k/\lambda$，$\lambda$为信号波长。由下图的等相位面可知，信号到达最左侧的阵元需要走更远的距离，因此，以最左侧的阵元为参考，即左侧阵元接收到的信号为$x_1(t)$，则其他阵元接收到的信号都滞后于它，此时，$x_1(t)=s(t),x_2(t)=s(t)e^{-j\varphi }$。如果，我们以最右侧信号为参考，即最右侧阵元接收到的信号为$x_1(t)$，则$x_1(t)=s(t),x_2(t)=s(t)e^{j\varphi }$。注意角度的正负号。

图2. 波程差示意图

接收信号写为向量形式：
$$Y(t)=\begin{array}{c}\left[\begin{array}{c}{y}_1(t)\\ y_2(t)\\ y_3(t)\\ ⋮\\ y_N(t)\end{array}\right]\end{array}$$
$y_i(t)$为第$i$个阵元接收到的信号，共有$N$个阵元。$X(t)=[s_1(t),s_2(t),\cdots ,s_D(t)]$，$s_i(t),1\le i\le D$，表示第$i$个信源发出的信号。$N(t)=[n_1(t),n_2(t),\cdots ,n_N(t){]}^T$，表示噪声，符合独立同分布的假设。
MUSIC算法的处理任务就是设法估计出入射到阵列的空间信号的个数$D$以及空间信号源的强度及其来波方向${\theta }_k$。
（2） 在实际处理中，$Y$得到的数据是有限时间段内的有限次数的样本（也称快拍或快摄），在这段时间内，假定来波方向不发生变化，且噪声为与信号不相关的白噪声，则定义阵列输出信号的二阶矩：$R_y$。

（3） MUSIC算法的核心就是对$R_y$进行特征值分解，利用特征向量构建两个正交的子空间，即信号子空间和噪声子空间。对$R_y$进行特征分解，即是使得图册中的公式成立。
（4） U是非负定的厄米特矩阵，所以特征分解得到的特征值均为非负实数，有D个大的特征值和M-D个小的特征值，大特征值对应的特征向量组成的空间Us为信号子空间，小特征值对应的特征向量组成的空间Un为噪声子空间。
（5） 将噪声特征向量作为列向量，组成噪声特征矩阵 ，并张成M-D维的噪声子空间Un，噪声子空间与信号子空间正交。而Us的列空间向量恰与信号子空间重合，所以Us的列向量与噪声子空间也是正交的，由此，可以构造空间谱函数。

（6） 在空间谱域求取谱函数最大值，其谱峰对应的角度即是来波方向角的估计值。

MUSIC算法MATLB仿真

% MUSIC空间谱估计算法仿真
close all; clear all; clc;
J=sqrt(-1); 
source_number=4; 
source_doa=[30 40 50 70]; 
sensor_number=7; 
snapshot_number=2000; 
snr=10; 
  
A=exp(-J*(0:sensor_number-1)'*pi*sin(source_doa*pi/180)); 
s=(randn(source_number,snapshot_number)+J*randn(source_number,snapshot_number))/sqrt(2); 
x=A*s; 
y=awgn(x,snr,'measured'); 
R=y*y'/snapshot_number; 
[V,D]=eig(R); 
Un=V(:,1:sensor_number-source_number); 
Gn=Un*Un'; 
  
searching_doa=0:0.1:90; 
for i=1:length(searching_doa) 
    a_theta=exp(-J*(0:sensor_number-1)'*pi*sin(pi*searching_doa(i)/180))
    P_con(i)=abs(a_theta'*R*a_theta);
    P_BF(i)=abs((a_theta'*R*a_theta)./(a_theta'*a_theta)); 
    P_capon(i)=1./abs((a_theta'*inv(R)*a_theta)); 
    P_music(i)=1./abs((a_theta'*Gn*a_theta)); 
end 
plot(searching_doa,P_con/max(P_con),'k');hold on;
plot(searching_doa,P_BF/max(P_BF),'r'); hold on;  
plot(searching_doa,P_capon/max(P_capon),'g'); hold on;
plot(searching_doa,P_music/max(P_music),'b'); hold off;grid on;
xlabel('ang');
ylabel('功率谱估计');
legend('conditional spectrum','Bartlett spectrum','Capon spectrum','Music spectrum');

仿真结果如下：

图3. 仿真结果

还有一种参考程序：

clear; close all;
%%%%%%%% MUSIC for Uniform Linear Array%%%%%%%%
derad = pi/180;      %角度->弧度
N = 8;               % 阵元个数        
M = 3;               % 信源数目
theta = [-30 0 60];  % 待估计角度
snr = 10;            % 信噪比
K = 512;             % 快拍数
 
dd = 0.5;            % 阵元间距 
d=0:dd:(N-1)*dd;
A=exp(-1i*2*pi*d.'*sin(theta*derad));  %方向矢量

%%%%构建信号模型%%%%%
S=randn(M,K);             %信源信号，入射信号
X=A*S;                    %构造接收信号
X1=awgn(X,snr,'measured'); %将白色高斯噪声添加到信号中
% 计算协方差矩阵
Rxx=X1*X1'/K;
% 特征值分解
[EV,D]=eig(Rxx);                   %特征值分解
EVA=diag(D)';                      %将特征值矩阵对角线提取并转为一行
[EVA,I]=sort(EVA);                 %将特征值排序 从小到大
EV=fliplr(EV(:,I));                % 对应特征矢量排序
                 
 
% 遍历每个角度，计算空间谱
for iang = 1:361
    angle(iang)=(iang-181)/2;
    phim=derad*angle(iang);
    a=exp(-1i*2*pi*d*sin(phim)).'; 
    En=EV(:,M+1:N);                   % 取矩阵的第M+1到N列组成噪声子空间
    Pmusic(iang)=1/(a'*En*En'*a);
end
Pmusic=abs(Pmusic);
Pmmax=max(Pmusic)
Pmusic=10*log10(Pmusic/Pmmax);            % 归一化处理
h=plot(angle,Pmusic);
set(h,'Linewidth',2);
xlabel('入射角/(degree)');
ylabel('空间谱/(dB)');
set(gca, 'XTick',[-90:30:90]);
grid on;

仿真结果如下：

图4. 仿真结果