作者简介:大家好,我是未央;
博客首页:未央.303
系列专栏:Java初阶数据结构
每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!!
文章目录
前言
一、二叉树的快速构建:
二、二叉树的遍历
2.1 前序遍历
2.2 中序遍历
2.3 后序遍历
2.4 层序遍历
三、其他一些常见操作
3.1 获取树中结点的个数
3.2 获取叶子结点的个数
3.3 获取第k层结点的个数
3.4 获取二叉树的高度
3.5 检测value结点是否存在
3.6 判断二叉树是不是完全二叉树
四、完整的代码
五、测试代码
测试结果:
总结
前言
上一小节我们学习了有关二叉树和树的基本性质和概念;对二叉树和树有了一些基本的认识;
本节内容我们将学习有关二叉树的基本操作,从代码的角度来深度认识二叉树;
一、二叉树的快速构建:
代码示例:
// 树类 public class MyBinaryTree { // 结点类 class TreeNode { public char val; // 储存该结点的数值 public TreeNode left; //左孩子的引用,即该结点的左子结点 public TreeNode right; //右孩子的引用 // 三种对树的结点的构造方法(每一种方法所传参数都是不同的) TreeNode() { } // 其实我们接下来用到的都是下面这一种构造方法,因为接下来我们只是在构造方法中给该结点赋值,至于该结点的左右子结点,我们是手动给他们建立联系的 TreeNode(char val) { this.val = val; } TreeNode(char val, TreeNode left, TreeNode right) { this.val = val; this.left = left; this.right = right; } @Override // 重写toString方法,一般接下来能够之间打印树的结点 public String toString() { return "TreeNode{" + "val=" + val + '}'; } } // 其实这不是二叉树真正的构建方式,但我们的目的是快速构建一个二叉树,学习的二叉树的一些方法(这是我们的侧重点) // 至于真正的构建方法,我们之后的博客会讲到,本篇博客我们重点了解二叉树所对应的各种独特的方法 public TreeNode createBinaryTree(){ TreeNode node1 = new TreeNode('A'); TreeNode node2 = new TreeNode('B'); TreeNode node3 = new TreeNode('C'); TreeNode node4 = new TreeNode('D'); TreeNode node5 = new TreeNode('E'); TreeNode node6 = new TreeNode('F'); TreeNode root = node1; // 我们采用了穷举法来快速的构建一棵二叉树 node1.left = node2; node1.right = node3; node2.left = node4; node2.right = node5; node3.left = node6; return root; // 返回我们构建树的根结点 } }

二、二叉树的遍历
学习二叉树结构,最简单的方式就是遍历。所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题(比如:打印节点内容、节点内容加1)
遍历是二叉树上最重要的操作之一,是二叉树上进行其它运算之基础;
大家想一下:在遍历二叉树时,如果没有进行某种约定,每个人都按照自己的方式遍历,得出的结果就比较混乱
但如果按照某种规则进行约定,则每个人对于同一棵树的遍历结果肯定是相同的。
如果N代表根节点,L代表根节点的左子树,R代表根节点的右子树,则根据遍历根节点的先后次序有以下遍历方式:
NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树
LNR:中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。
LRN:后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点代码:
// 前序遍历 void preOrder(TreeNode root); // 中序遍历 void inOrder(TreeNode root); // 后序遍历 void postOrde(TreeNode root);
2.1 前序遍历
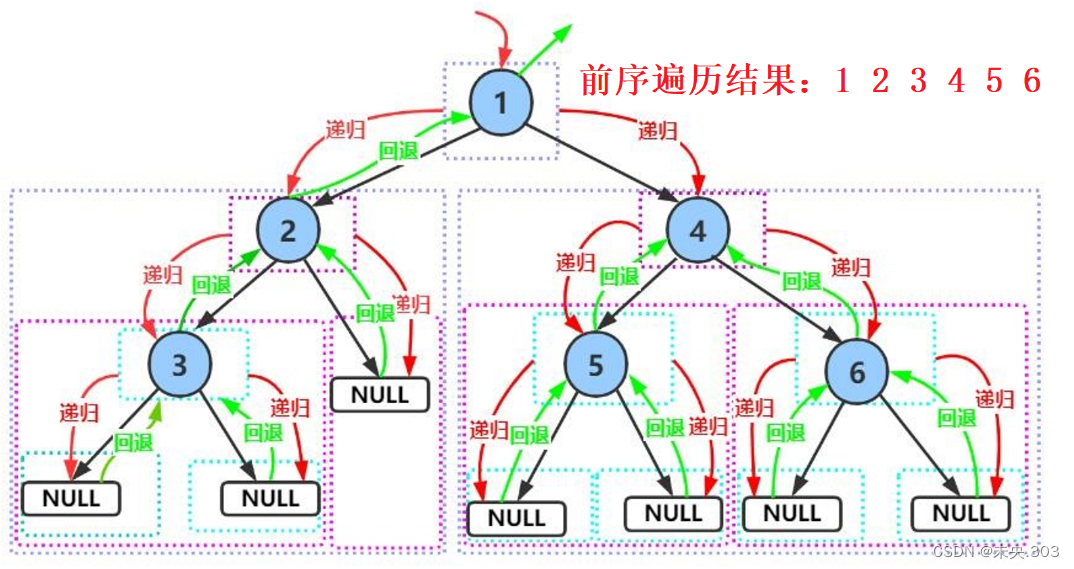
比如这样一棵树
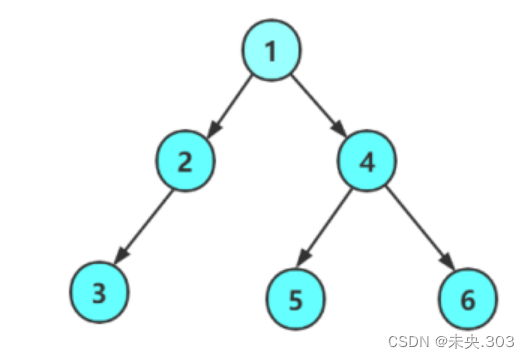
它的前序遍历顺序就是:1->2->3->4->5->6;
对应的代码:
// 前序遍历——》根->左子树->右子树 public void preOrder(TreeNode root) { if (root == null) return; System.out.print(root.val + " "); preOrder(root.left); preOrder(root.right); }代码解析:
前序遍历(Preorder Traversal 亦称先序遍历)—访问根结点—>根的左子树—>根的右子树。我们利用递归解决问题的思想, 可以将一个问题拆解为子问题去解决, 也就是实现下面的过程:
- 访问根节点数据;
- 前序遍历左子树;
- 前序遍历右子树;
递归结束条件:如果结点root为空,则返回。
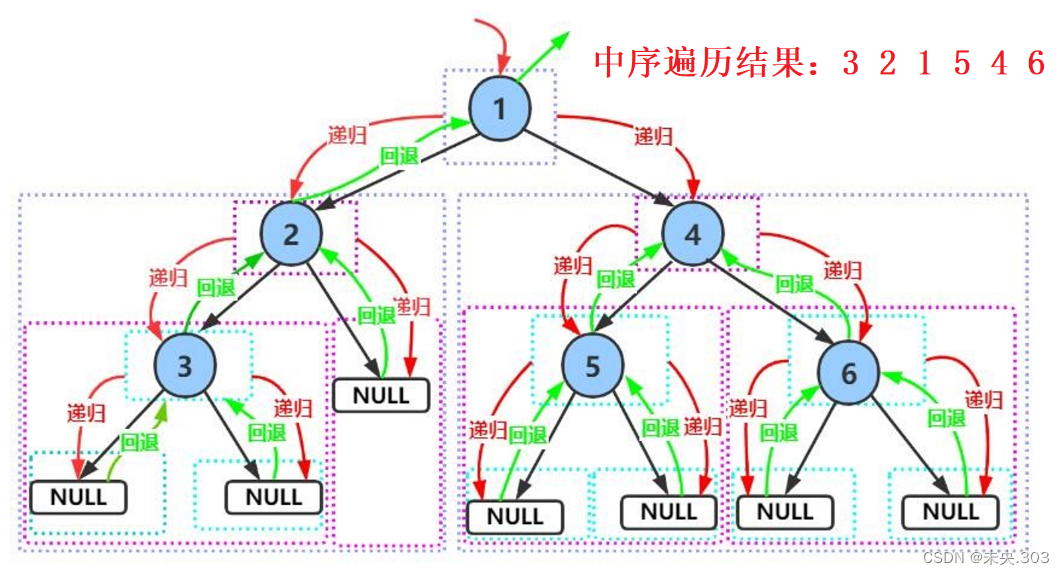
2.2 中序遍历
核心思想是一样的,只是顺序变了,先处理左子树,再处理左右子树所对应的根结点,最后再处理右子树;
对应代码:
// 中序遍历——》左子树—>根->右子树 public void inOrder(TreeNode root) { if (root == null) return; inOrder(root.left); System.out.print(root.val + " "); inOrder(root.right); }代码解析:
中序遍历(Inorder Traversal)——根的左子树—>根节点—>根的右子树;
和上面的实现思想相同, 只是访问根节点的时机不同;
- 中序遍历左子树;
- 访问根节点数据;
- 中序遍历右子树;
递归结束条件:如果结点root为空,则返回。
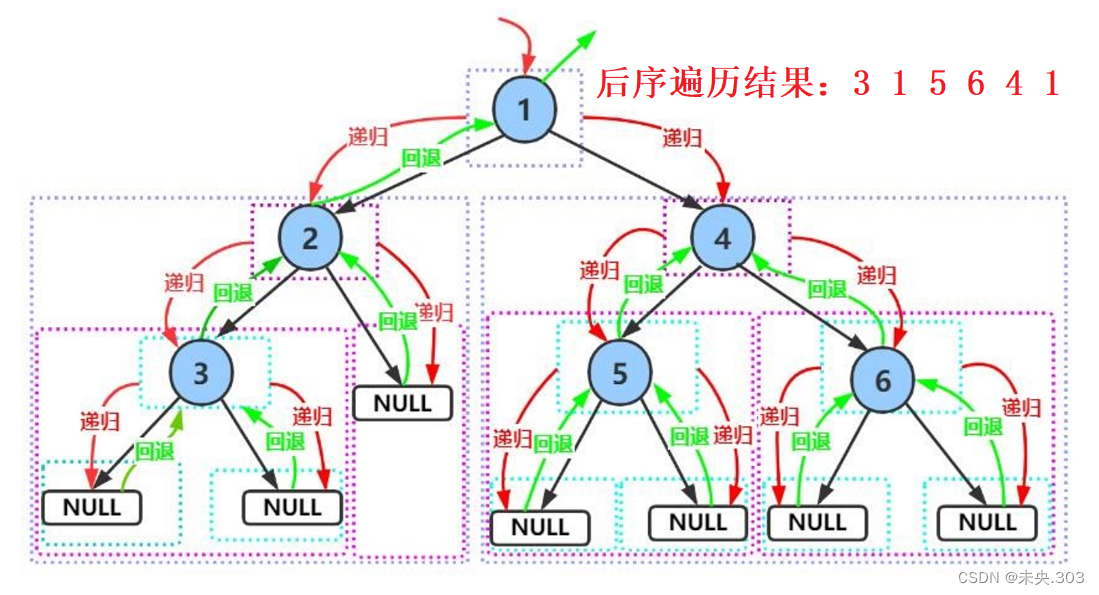
2.3 后序遍历
对应代码:
// 后续遍历——》左子树->右子树—>根 public void postOrder(TreeNode root) { if (root == null) return; postOrder(root.left); postOrder(root.right); System.out.print(root.val + " "); }代码解析:
同样的, 实现过程如下,
- 后序遍历左子树;
- 后序遍历右子树;
- 访问根结点数据;
递归结束条件:如果结点root为空,则返回。
2.4 层序遍历
定义:
设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
对应代码:
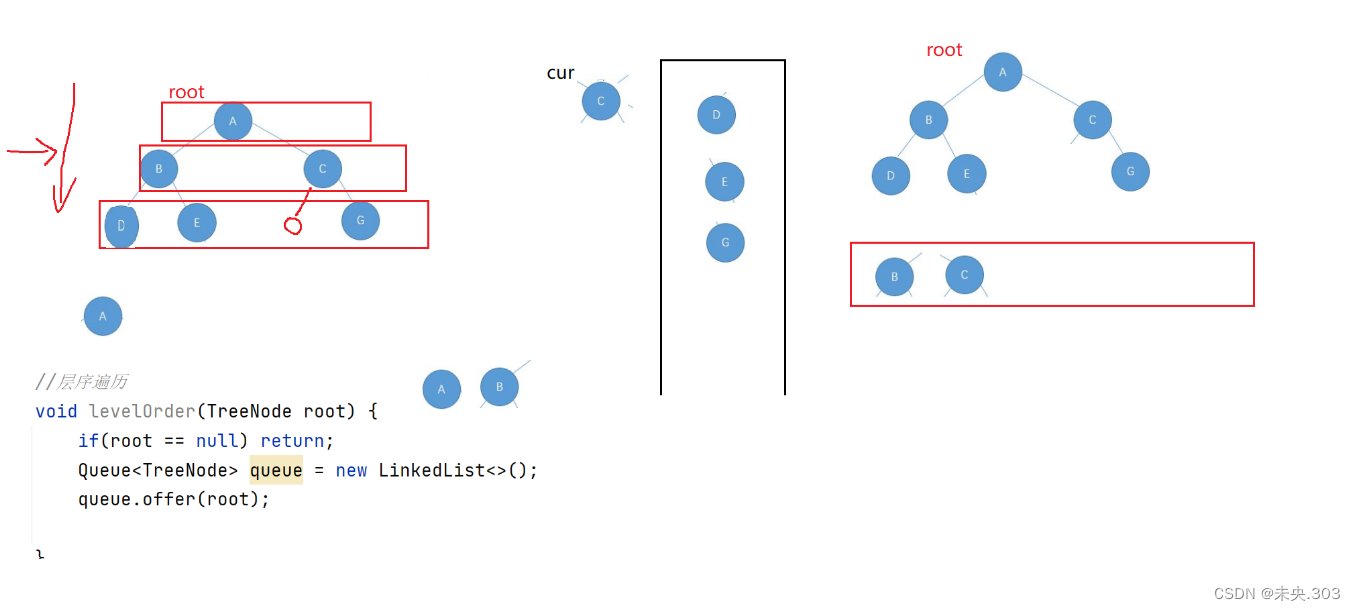
//层序遍历 public void levelOrder(TreeNode root) { if(root == null) return; Queue<TreeNode> queue = new LinkedList<>(); // 我们需要借助一个队列, queue.offer(root); // 先把根结点放到队列中,根结点相当于是第一层 while (!queue.isEmpty()) { // 借助tmp来把当前结点的左右子树给放到队列中 // 注意随着队列元素的不断弹出,tmp是在动态变化的,所以才能变量完——整棵二叉树 TreeNode tmp = queue.poll(); // 因为这一层的元素入队列的时候,是通过上一层元素的对左右子树操作来实现的,入队列是一层一层入的 System.out.print(tmp.val + " "); if (tmp.left != null) { queue.offer(tmp.left); // 把当前从队列中弹出的结点的左子结点放到队列中 } if (tmp.right != null) { queue.offer(tmp.right); // 右子结点 } } }代码解析:
首先我们需要借助一个队列;先把根结点放到队列中,根结点相当于是第一层;
层序遍历的实现方式与判断一棵二叉树是否是完全二叉树类似,都是使用队列来进行实现,只有一点不同, 入队时如果结点为空,则不需要入队,其他的地方完全相同, 出队时获取到节点中的元素, 直到最终队列和当前结点均为空时,表示遍历结束。
图示说明:
视频解析记录:二叉树02;(02:51:57)

三、其他一些常见操作
3.1 获取树中结点的个数
// 获取树的结点的个数,遍历 public static int nodeSize; void size2(TreeNode root) { if (root == null) return; ++nodeSize; size2(root.left); size2(root.right); }代码解析:
由于节点的个数等于根节点(1) + 左子树节点个数 + 右子树节点个数 ;先创立一个结点nodesize记录结点大小;
我们首先建立递归size2();当root==null时,说明此处没有结点;
递归结束条件: 如果结点root为空,则返回。
当root!=null时,说明此处有结点,所以nodesize++;
最后分别遍历左子树,右子树;最终得到结点的总个数;
视频解析记录:二叉树02;(47:30);
递归的大致流程如图所示:
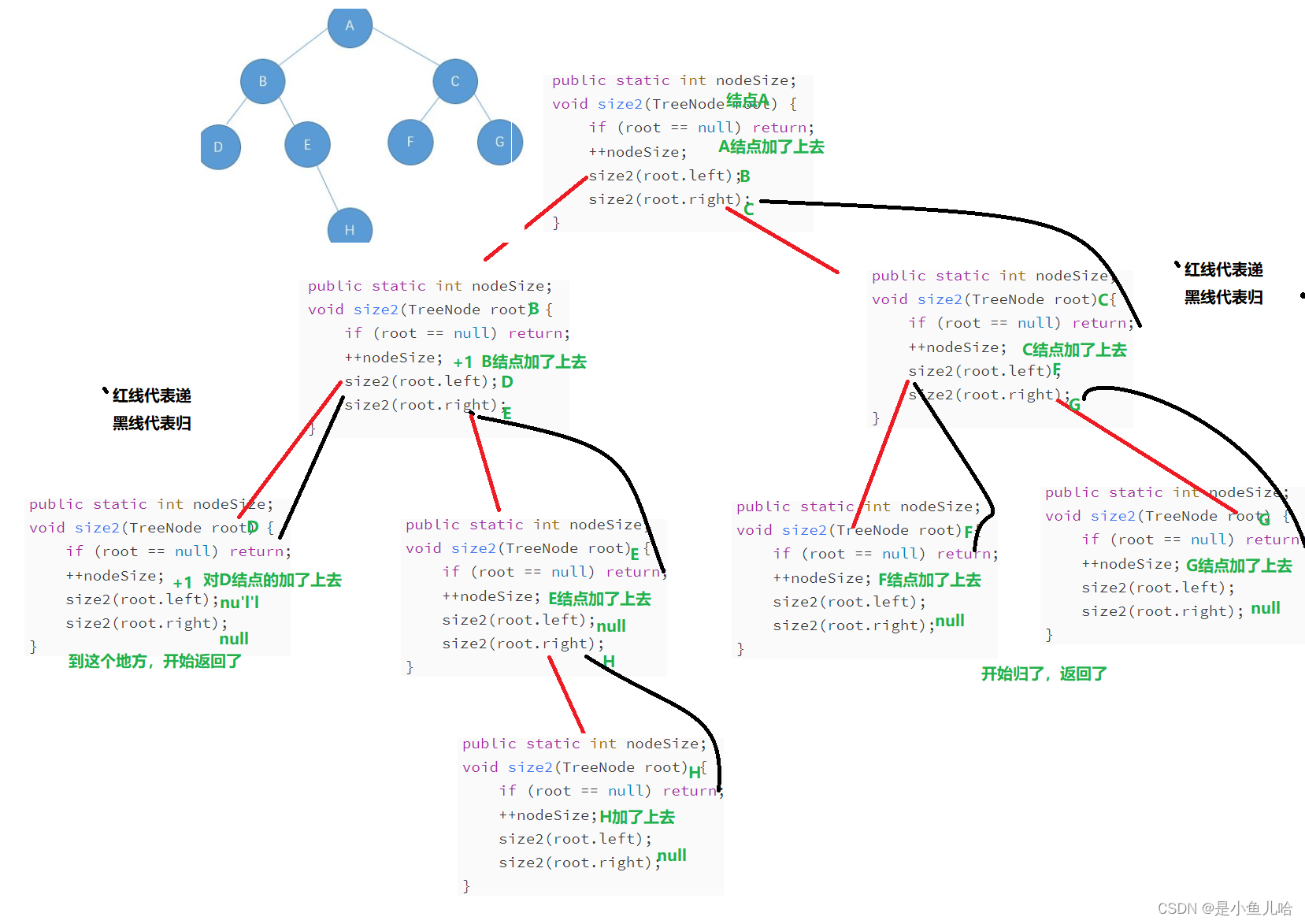
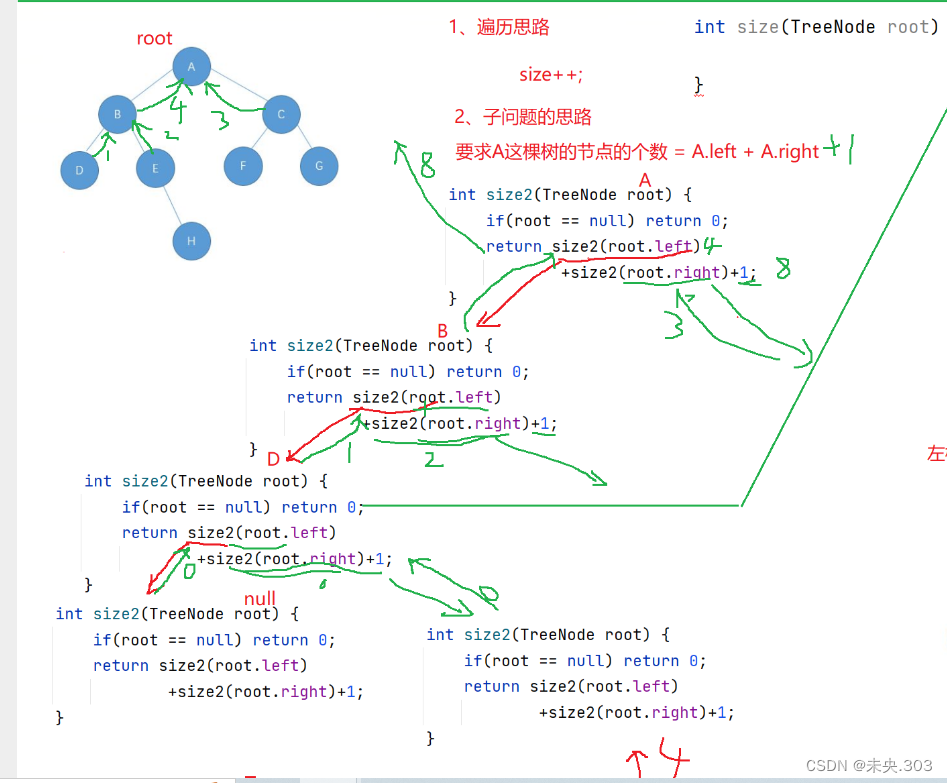
解法2:递归,转换为左右子问题求解:
// 获取树中节点的个数,子问题求解 int size(TreeNode root) { if (root == null) return 0; int leftSize = size(root.left); // 递归到root.left == null 开始返回:return 0; int rightSize = size(root.right); // 当leftSize和rightSize都第一次递归结束(即道理叶结点出,此时叶子结点的左右子节点都为空之间返回0,但你能说结点为0吗 // 肯定不能虽然当前结点的左右子结点数目都为0,但别忘了当前结点也是算一个结点呀!!!所以要+1 return leftSize + rightSize + 1;//加1是因为头结点也是一个结点 }图示解析:
视频解析定位:二叉树02;(52:35)
3.2 获取叶子结点的个数
// 遍历思路—获取叶子节点的个数 public static int leafSize; // 因为getLeafNodeCount1函数中有递归,所以我们的nodeSize不能定义到函数里 // (因为递归不断调用我们的函数,相当于会给nodeSize不断的赋初始值,所以我们对nodeSize累加的值会被冲掉 int getLeafNodeCount1(TreeNode root){ if (root == null) return 0; if (root.left == null && root.right == null) { ++leafSize; } getLeafNodeCount1(root.left); // 其实遍历也离不开递归 getLeafNodeCount1(root.right); return leafSize; }代码解析:
递归思路:
- 如果结点为空,表示该树没有结点返回0,
- 如果结点的左右子树都为空,表示该结点为叶子结点,计算器+1或者返回1。
- 一棵二叉树的叶子结点数为左右子树叶子结点数之和。(分别递归左右子树)
视频解析定位:二叉树02(01:09:26)
解法2:子问题思路
// 子问题思路-求叶子结点个数 int getLeafNodeCount2(TreeNode root) { if (root == null) return 0; if (root.left == null && root.right == null) return 1;//如果左右子树都为空的话,说明只有一个根节点,并且也是一个叶子结点; return getLeafNodeCount2(root.left) + getLeafNodeCount2(root.right); // 返回左子树的叶子结点的个数 + 右子树叶子结点的个数 }代码解析:
递归思路:
- 如果结点为空,表示该树没有结点返回0,
- 如果结点的左右子树都为空,表示该结点为叶子结点,计算器+1或者返回1。
- 一棵二叉树的叶子结点数为左右子树叶子结点数之和。(一起递归左右子树)
视频解析定位:二叉树02(01:20:12)
3.3 获取第k层结点的个数
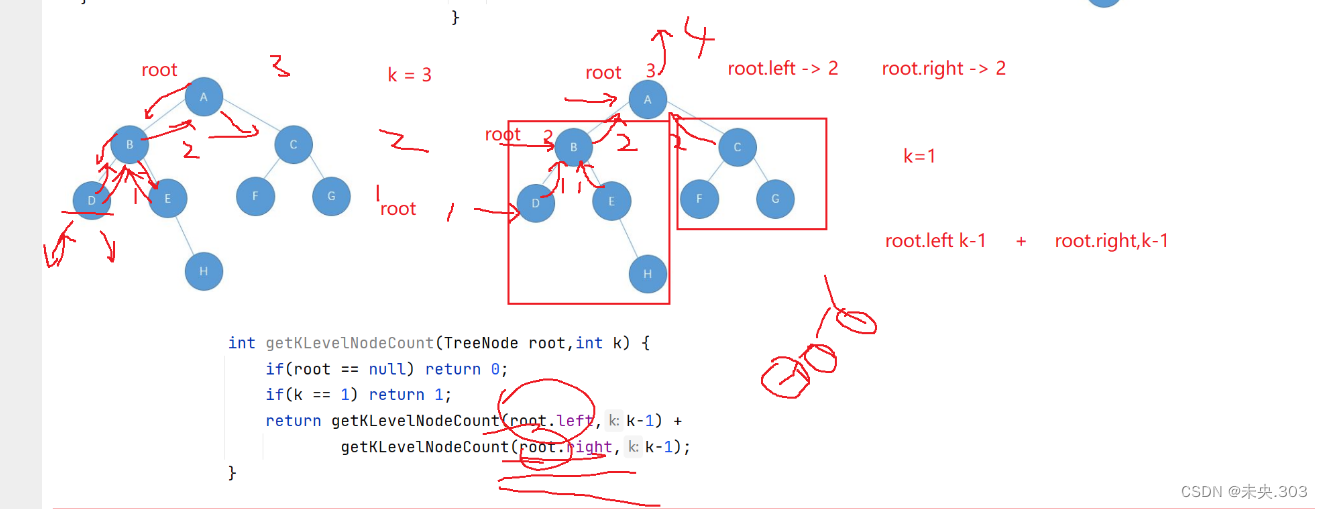
// 获取第K层节点的个数 int getKLevelNodeCount(TreeNode root, int k) { if (root == null) return 0; if (k == 1) return 1; return getKLevelNodeCount(root.left, k - 1) + getKLevelNodeCount(root.right, k - 1); }代码解析:
递归思路:
- 如果结点为空,返回0,k为1,返回1。
- 一棵二叉树第k层结点数为 左子树和右子树第k-1层次的结点数之和。
当k=1时,表示第一层次的结点个数,结点个数为1,每递归一层,从根节点来说是第k层, 那么相对于根节点的子树来说就是k-1层,所以一棵二叉树第k层结点数为左子树,右子树第k-1层次的结点数之和。
图示说明:
视频解析定位:二叉树02(01:44:03)
3.4 获取二叉树的高度
递归思路,二叉树天生就适合递归,因为二叉树的定义就用到了递归的概念 ;
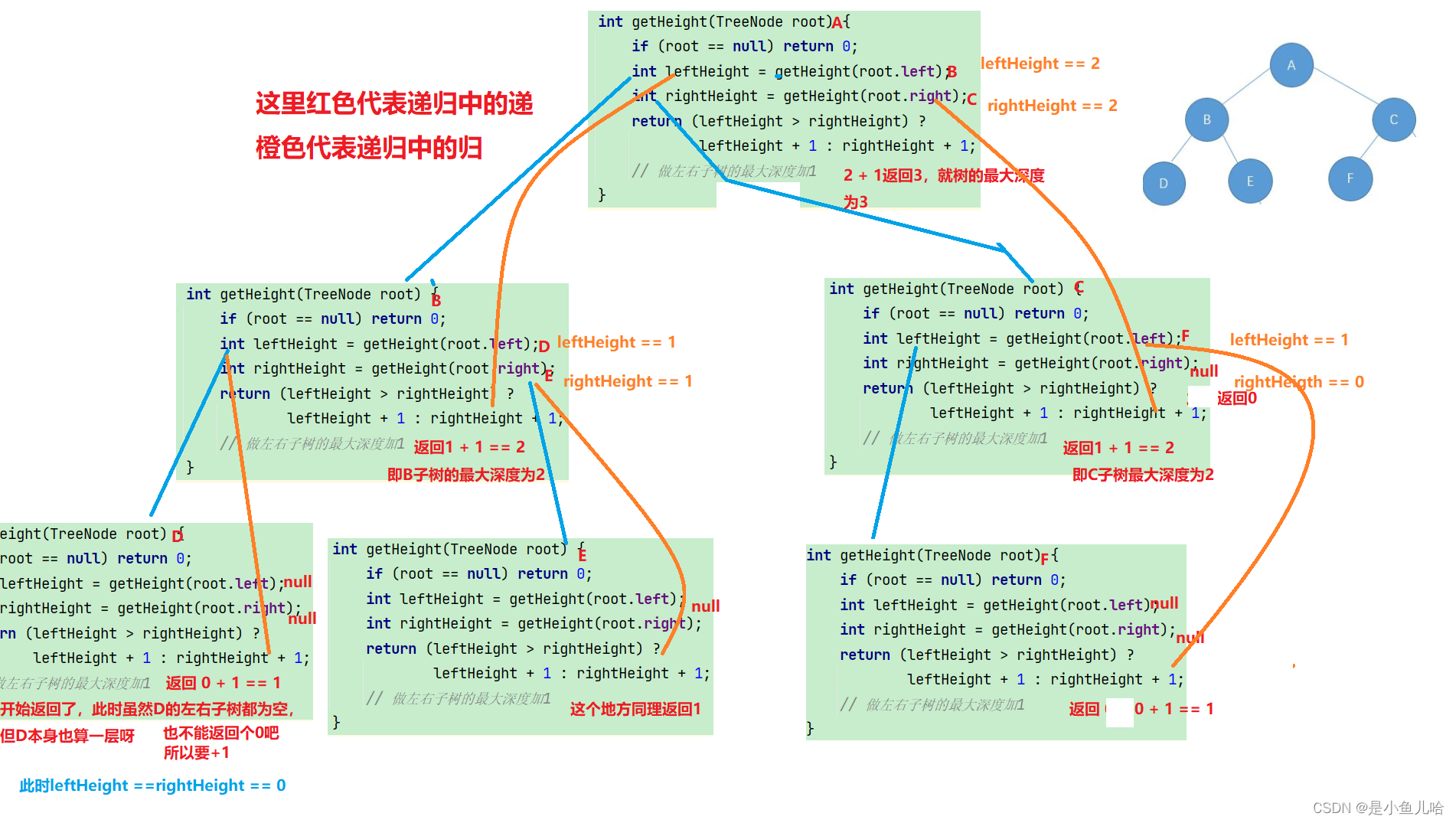
// 获取二叉树的高度——时间复杂度O(N) int getHeight(TreeNode root) { if (root == null) return 0; // 下面这样写虽然对,但应为多递归了一次;在oj上可能超时 //return (getHeight(root.left) > getHeight(root.right)) ? getHeight(root.left) + 1 : getHeight(root.right) + 1; // 所以这样写,用变量把我们递归的结果保存下来,这样在三目运算符?后就不用在重复的调用递归求高度了 int leftHeight = getHeight(root.left); int rightHeight = getHeight(root.right); return (leftHeight > rightHeight) ? leftHeight + 1 : rightHeight + 1; // 做左右子树的最大深度加1 }代码解析:
递归思路:
- 如果根结点为空,则这棵树的高度为0,返回0。
- 一棵二叉树的最深深度即为左右子树深度中较大的值加上1。
图示说明:
视频解析定位:二叉树02(01:56:29)
3.5 检测value结点是否存在
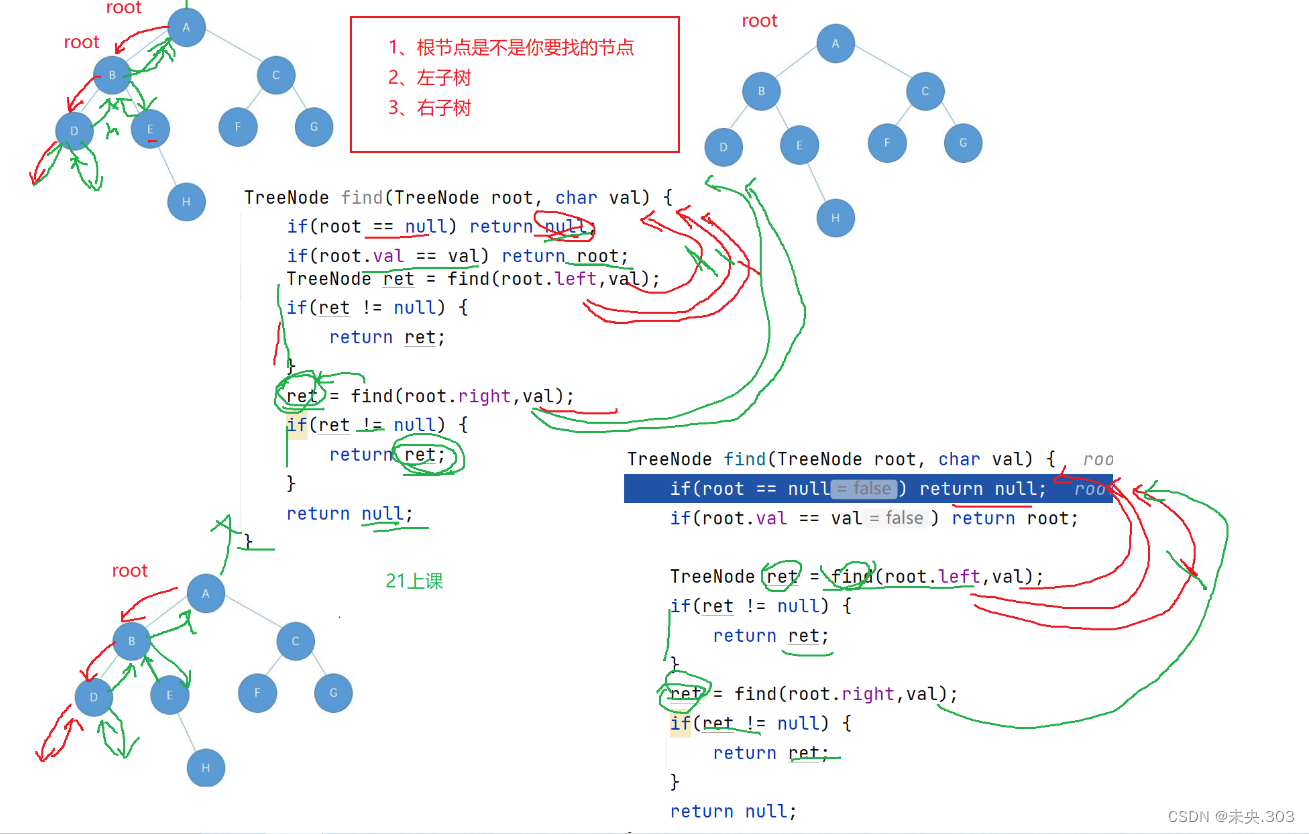
// 检测值为value的元素是否存在——转换为子问题 TreeNode find(TreeNode root, char val) { if(root == null) return null; if(root.val == val) return root; TreeNode treeNode1 = find(root.left, val); TreeNode treeNode2 = find(root.right, val); if (treeNode1 == null) return treeNode2; else return treeNode1; }代码解析:
通过遍历去搜索比较即可, 前中后序遍历都可以;
递归思路:
- 首先判断根节点是不是你要找的结点;
- 然后在左子树查找有没有你想要的结点;
- 然后查找右子树有没有你想要的结点;
图示说明:
视频解析定位:二叉树02(02:29:24)
3.6 判断二叉树是不是完全二叉树
//判断一棵树是不是完全二叉树 public boolean isCompleteTree(TreeNode root) { if(root == null) { return true; } Queue<TreeNode> queue = new LinkedList<>(); queue.offer(root); while(!queue.isEmpty()) { TreeNode cur = queue.poll(); if(cur == null) { break; } queue.offer(cur.left); queue.offer(cur.right); } //判断队列中是否有不为空的元素 int size = queue.size(); while(size != 0) { size--; if(queue.poll() != null) { return false; } } return true; }代码解析:
判断一棵树是不是完全二叉树,我们可以设计一个队列来实现;
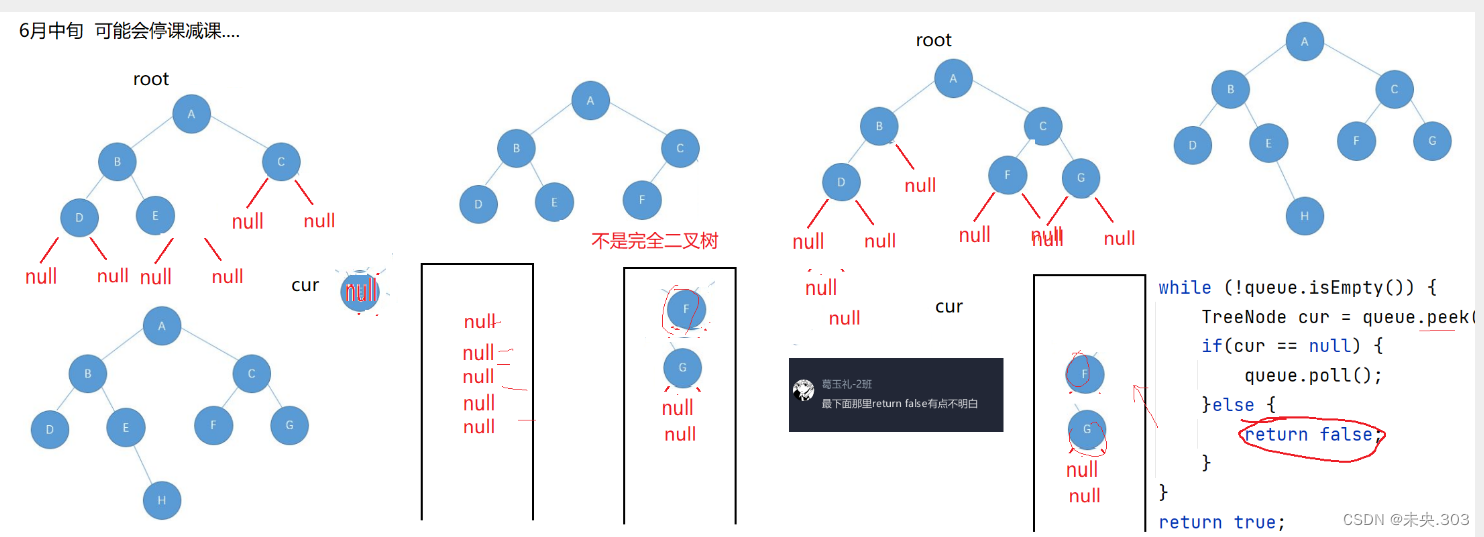
完全二叉树按照从上至下, 从左到右的顺序节点之间是连续着没有空位置的, 这里如果有不了解的可以看一看二叉树概念篇的博客; 如果一颗二叉树不是完全二叉树 , 那么树中的节点之间是有空着的位置的(null); 只要找到这个位置, 后面再没有节点了就是完全二叉树; 如果空位置后面还有节点就不是完全二叉树;
我们可以设计一个队列来实现, 首先将根节点入队,然后循环每次将队头元素出队同时将出队节点的左右孩子结点(包括空结点)依次入队,以此类推,直到获取的结点为空(就是上面说的空位置),此时判断队列中的所有元素是否为空,如果为空,就表示这棵二叉树为完全二叉树 ; 否则就不是完全二叉树;
图示说明:
视频解析定位:二叉树02(06:43)
四、完整的代码
import java.util.ArrayList; import java.util.LinkedList; import java.util.List; import java.util.Queue; // 树类 public class MyBinaryTree { // 结点类 class TreeNode { public char val; // 储存该结点的数值 public TreeNode left; //左孩子的引用,即该结点的左子结点 public TreeNode right; //右孩子的引用 // 三种对树的结点的构造方法(每一种方法所传参数都是不同的) TreeNode() { } // 其实我们接下来用到的都是这一种构造方法,因为接下来我们只是在构造方法中给该结点赋值,至于该结点的左右子结点,我们是手动给他们建立联系的 TreeNode(char val) { this.val = val; } TreeNode(char val, TreeNode left, TreeNode right) { this.val = val; this.left = left; this.right = right; } @Override // 重写toString方法,一般接下来能够之间打印树的结点 public String toString() { return "TreeNode{" + "val=" + val + '}'; } } // 其实这不是二叉树真正的构建方式,但我们的目的是快速构建一个二叉树,学习的二叉树的一些方法(这是我们的侧重点) // 至于真正的构建方法,我们之后的博客会讲到,本篇博客我们重点了解二叉树所对应的各种独特的方法 public TreeNode createBinaryTree(){ TreeNode node1 = new TreeNode('A'); TreeNode node2 = new TreeNode('B'); TreeNode node3 = new TreeNode('C'); TreeNode node4 = new TreeNode('D'); TreeNode node5 = new TreeNode('E'); TreeNode node6 = new TreeNode('F'); TreeNode root = node1; // 我们采用了穷举法来快速的构建一棵二叉树 node1.left = node2; node1.right = node3; node2.left = node4; node2.right = node5; node3.left = node6; return root; // 返回我们构建树的根结点 } // 前序遍历——》根->左子树->右子树 public void preOrder(TreeNode root) { if (root == null) return; System.out.print(root.val + " "); postOrder(root.left); postOrder(root.right); } // 中序遍历——》左子树—>根->右子树 public void inOrder(TreeNode root) { if (root == null) return; inOrder(root.left); System.out.print(root.val + " "); inOrder(root.right); } // 后续遍历——》左子树->右子树—>根 public void postOrder(TreeNode root) { if (root == null) return; postOrder(root.left); postOrder(root.right); System.out.print(root.val + " "); } // 获取树的结点的个数,遍历 public static int nodeSize; void size2(TreeNode root) { if (root == null) return; ++nodeSize; size2(root.left); size2(root.right); } // 获取树中节点的个数,子问题求解 int size(TreeNode root) { if (root == null) return 0; int leftSize = size(root.left); // 递归到root.left == null 开始返回:return 0; int rightSize = size(root.right); // 当leftSize和rightSize都第一次递归结束(即道理叶结点出,此时叶子结点的左右子节点都为空之间返回0,但你能说结点为0吗 // 肯定不能虽然当前结点的左右子结点数目都为0,但别忘了当前结点也是算一个结点呀!!!所以要+1 return leftSize + rightSize + 1; } // 遍历思路—获取叶子节点的个数 public static int leafSize; // 因为getLeafNodeCount1函数中有递归,所以我们的nodeSize不能定义到函数里 // (因为递归不断调用我们的函数,相当于会给nodeSize不断的赋初始值,所以我们对nodeSize累加的值会被冲掉 int getLeafNodeCount1(TreeNode root){ if (root == null) return 0; if (root.left == null && root.right == null) { ++leafSize; } getLeafNodeCount1(root.left); // 其实遍历也离不开递归 getLeafNodeCount1(root.right); return leafSize; } // 子问题思路-求叶子结点个数 int getLeafNodeCount2(TreeNode root) { if (root == null) return 0; if (root.left == null && root.right == null) return 1; return getLeafNodeCount2(root.left) + getLeafNodeCount2(root.right); // 返回左子树的叶子结点的个数 + 右子树叶子结点的个数 } // 获取第K层节点的个数 int getKLevelNodeCount(TreeNode root, int k) { if (root == null) return 0; if (k == 1) return 1; return getKLevelNodeCount(root.left, k - 1) + getKLevelNodeCount(root.right, k - 1); } // 获取二叉树的高度——时间复杂度O(N) int getHeight(TreeNode root) { if (root == null) return 0; // 下面这样写虽然对,但应为多递归了一次;在oj上可能超时 //return (getHeight(root.left) > getHeight(root.right)) ? getHeight(root.left) + 1 : getHeight(root.right) + 1; // 所以这样写,用变量把我们递归的结果保存下来,这样在三目运算符?后就不用在重复的调用递归求高度了 int leftHeight = getHeight(root.left); int rightHeight = getHeight(root.right); return (leftHeight > rightHeight) ? leftHeight + 1 : rightHeight + 1; // 做左右子树的最大深度加1 } // 检测值为value的元素是否存在——转换为子问题 TreeNode find(TreeNode root, char val) { if(root == null) return null; if(root.val == val) return root; TreeNode treeNode1 = find(root.left, val); TreeNode treeNode2 = find(root.right, val); if (treeNode1 == null) return treeNode2; else return treeNode1; } //层序遍历 public void levelOrder(TreeNode root) { if(root == null) return; Queue<TreeNode> queue = new LinkedList<>(); // 我们需要借助一个队列, queue.offer(root); // 先把根结点放到队列中,根结点相当于是第一层 while (!queue.isEmpty()) { // 借助tmp来把当前结点的左右子树给放到队列中 // 注意随着队列元素的不断弹出,tmp是在动态变化的,所以才能变量完——整棵二叉树 TreeNode tmp = queue.poll(); // 因为这一层的元素入队列的时候,是通过上一层元素的对左右子树操作来实现的,入队列是一层一层入的 System.out.print(tmp.val + " "); if (tmp.left != null) { queue.offer(tmp.left); // 把当前从队列中弹出的结点的左子结点放到队列中 } if (tmp.right != null) { queue.offer(tmp.right); // 右子结点 } } } // 力扣oj题目——层序遍历,因为要求不同所以我们的具体做法有些不一样,但基本的思想相同 public List<List<Character>> levelOrder1(TreeNode root) { List<List<Character>> ret = new ArrayList<>(); if (root == null) return ret; // Queue<TreeNode> queue = new LinkedList<>(); queue.offer(root); // 首先根结点先入队 while (!queue.isEmpty()) { int size = queue.size(); // 第一层的size = 1; List<Character> ans = new ArrayList<>(); while (size != 0) { TreeNode tmp = queue.poll(); ans.add(tmp.val); // 把当前从栈中出来的元素放到我们定义的List中,因为是同一层的,在一个循环里的 if (tmp.left != null) { queue.offer(tmp.left); } if (tmp.right != null) { queue.offer(tmp.right); } --size; } ret.add(ans); } return ret; } }

五、测试代码
public class TestMyBinaryTree { public static void main(String[] args) { MyBinaryTree myBinaryTree = new MyBinaryTree(); MyBinaryTree.TreeNode root = myBinaryTree.createBinaryTree(); myBinaryTree.size2(root); System.out.println(MyBinaryTree.nodeSize); System.out.print("前序遍历的结果是:"); myBinaryTree.preOrder(root); // 前序遍历 System.out.println(); System.out.print("中序遍历的结果是:"); myBinaryTree.inOrder(root); // 中序遍历 System.out.println(); System.out.print("后序遍历的结果是:"); myBinaryTree.postOrder(root); // 后序遍历 System.out.println(); System.out.println("=========我是分割线========="); System.out.println("在树中,对B的查找结果是:" + myBinaryTree.find(root, 'B')); System.out.println("在树中,对d的查找结果是:" + myBinaryTree.find(root, 'd')); System.out.println("当前树中的最大深度为:" + myBinaryTree.getHeight(root)); System.out.println("=========我是分割线========="); System.out.println("当前树中的结点个数是:" + myBinaryTree.size(root)); System.out.println("当前树中的叶子结点个数:" + myBinaryTree.getLeafNodeCount1(root)); System.out.println("当前树中第2层的结点个数为:" + myBinaryTree.getKLevelNodeCount(root, 2)); System.out.print("层序遍历的结果为:"); myBinaryTree.levelOrder(root); } }
测试结果:
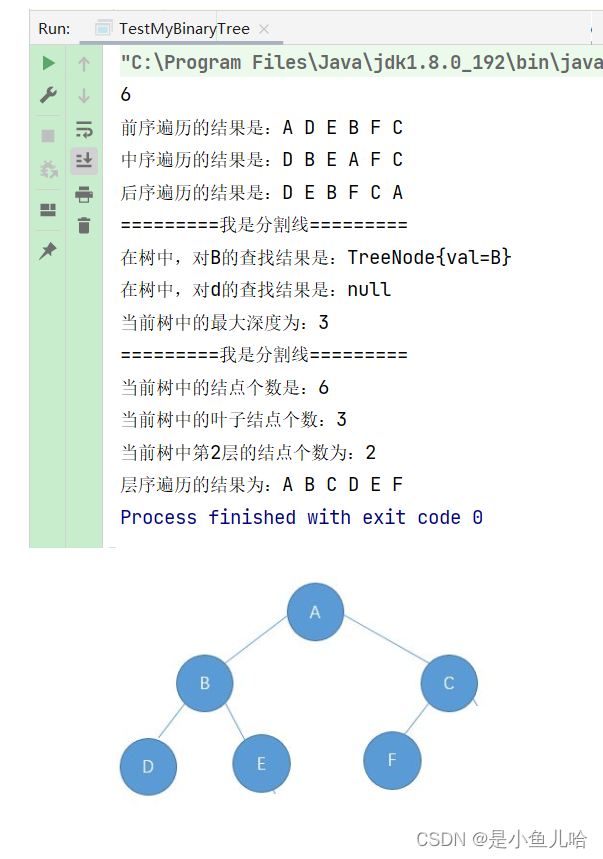
总结
今天的内容就介绍到这里,我们下一节内容再见!!!!!!!!!!!!!!!!!!


![[Linux]文件系统权限与访问控制](https://img-blog.csdnimg.cn/214df36c7c7141899696348f6bdaf236.png)